Связь расстояния Хэмминга и корректирующих свойств кода

Количество обнаруживаемых и исправляемых кодом ошибок связано с его минимальным кодовым расстоянием d₀.

Обозначим число (кратность) ошибок, обнаруживаемых в одной кодовой комбинации, через t_о, а число исправляемых ошибок в одной кодовой комбинации - через t_и. Ошибка не обнаруживается, если одна разрешенная комбинация переходит в другую разрешенную. Следовательно, для обеспечения возможности обнаружения всех ошибок кратностью до t_о включительно необходимо, чтобы кодовое расстояние определялось неравенством

Поясним данное соотношение с помощью рисунка:

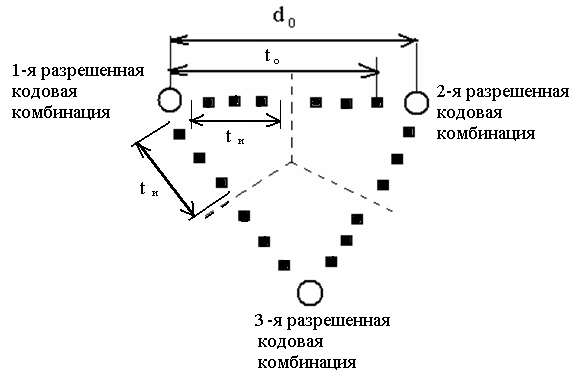
На рисунке - окружности соответствуют разрешенным комбинациям, зачерненные квадраты – разряды, разделяющие разрешенные кодовые комбинации.

Для обеспечения возможности исправления всех ошибок крат­ности до t_и включительно необходимо, чтобы принятая кодовая комбинация осталась в подмножест­ве запрещенных комбинаций, которое ей принадлежит (на рисунке эти подмножества отделены пунктирными линиями). В этом слу­чае кодовое расстояние

Т.е., если код исправляет все ошибки кратностью t_и, то число ошибок, которые он может обнаружить, равно t_о = 2t_и. Чтобы код обнаруживал ошибки кратностью t_о и, исправлял ошибки кратностью t_и, кодовое расстояние должно быть равно

На самом деле обнаруживаться и ис­правляться будут ошибки и большей кратности, поскольку рас­стояние между отдельными кодовыми комбинациями может быть больше чем d₀. Однако процент исправляемых ошибок невелик.

Определение требуемого числа проверочных разрядов

Необходимое кодовое расстояние d_o, а значит, и корректирую­щая способность кода определяются его относительной избыточ­ностью, под которой понимают отношение

где r - число избыточных (проверочных) разрядов,

n - общее число разрядов в кодовой комбинации.

Очевидно, что количество дополнительных разрядов r связано с кодовым расстоянием d₀. Кодовое расстояние будет тем боль­шим, чем больше избыточность кода и чем равномернее распреде­лены расстояния между разрешенными кодовыми комбинациями. Однако точных формул, связывающих величины r и d₀ нет. Такая формула известна только для кода с d₀=3:

Откуда имеем: где n=k+r.

Для остальных случаев известны только верхние и нижние оценки кодового расстояния:

1. Граница Плоткина дает верхнюю грани­цу кодового расстояния d₀ при заданном основании кода R, числе разрядов в кодовой комбинации n и числе информационных раз­рядов k:

для двоичных кодов

2. Граница Варшамова—Гильберта определяет нижнюю границу для числа проверочных разрядов, необходимого для обеспечения за­данного кодового расстояния d₀:

где - число сочетаний из n-1 элементов по i элементам.