Связь порождающей и проверочной матриц кода Хэмминга

Сравним составленные для кода (9,5) проверочную и порождающую матрицы:

Заметим, что правая подматрица порождающей матрицы G (на рисунке - заштрихована) и левая подматрица проверочной матрицы H (на рисунке также заштрихована) связаны между собой.

Сравним заштрихованные части:

1. Шестой столбец матрицы G есть первая строка матрицы H.

2. Седьмой столбец матрицы G есть вторая строка матрицы H.

3. Восьмой столбец матрицы G есть третья строка матрицы H.

4. Девятый столбец матрицы G есть четвертая строка матрицы H.

Можно сделать вывод, что правая подматрица матрицы G является транспонированной по отношению к левой подматрице матрицы H.

Следовательно, порождающая матрица G, как и проверочная матрица H представляет собой запись в компактной форме соотношений для нахождения проверочных элементов b_i:

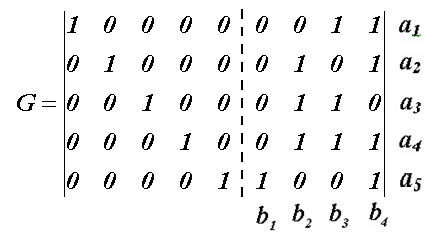
Учитывая обозначения на рисунке, показывающие соответствия между столбцами, строками, информационными и проверочными элементами, запишем выражения для формирования проверочных элементов b_i:

b₁=a₅;

Очевидно, что полученные выражения полностью совпадают с полученными ранее.

Матричное построение систематических кодов с поэлементным формированием проверочной группы

Код Хэмминга относится к систематическим кодам с поэлементным формированием проверочной группы. Любой код этой группы может быть задан своей порождающей или проверочной матрицами. Т.к. между порождающей и проверочной матрицами существует однозначное соответствие, то безразлично, какой из них задавать код.

Чаще используется проверочная матрица, т.к. она позволяет легко определить кодовое расстояние Хэмминга.

Правило: расстояние Хэмминга на единицу больше минимального веса столбцов правой части подматрицы матрицы H.

Пример

Найти расстояние Хэмминга, если проверочная матрица кода имеет вид:

Определяем вес столбцов в правой части матрицы H (правая часть отделена пунктирной линией). Имеем:

(Вес столбца определяется как вес кодовой комбинации, он равен числу единиц в этом столбце).

Из найденных значений выбираем минимальное:

Тогда

Дуальные коды

Рассматривая матрицы G и H, можно заметить, что каждая из них содержит множество линейно независимых векторов и скалярное произведение каждой строки матрицы G на каждую строку матрицы H равно нулю, то есть

H× G^T = 0 и G× H^T = 0 .

Следовательно, можно "поменять ролями" эти две матрицы и использовать Н как порождающую матрицу, а G как проверочную матрицу некоторого другого кода.

Коды, связанные таким образом, называются дуальными друг другу, т.е., задав каким-либо образом линейный блочный код, автоматически задается и второй, дуальный ему код. Но, если исходный код был получен так, чтобы иметь минимальную избыточность при заданной исправляющей способности, то гарантировать хорошее качество дуального ему кода нельзя. Дуальный код обычно имеет исправляющую способность, одинаковую с исходным, но большую, чем у него, избыточность.

Например, если рассмотренный в качестве примера код Хемминга (9,5) имеет 4 избыточных элемента и при этом позволяет исправлять одну ошибку в кодовом слове из 9 символов, то дуальный ему код (9,4) также исправляет одну ошибку на 9 символов, но уже имеет 5 избыточных элементов, то есть на 4 информационных символа содержит 5 проверочных.