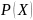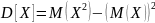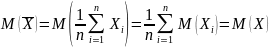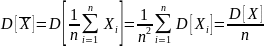- •Основные понятия теории вероятностей. События
- •Классификация событий.
- •Операции над событиями.
- •Классическое определение вероятности случайного события
- •Статистическое определение вероятности
- •Геометрическая вероятность
- •Аксиомы теории вероятностей.
- •Зависимые и независимые случайные события. Основные формулы сложения и умножения вероятностей
- •Теоремы сложения вероятностей
- •Зависимые и независимые события. Условная вероятность.
- •Формулы умножения вероятностей
- •Формула полной вероятности
- •Одномерные случайные величины
- •Понятие случайной величины
- •Законы распределения случайной величины
- •Функция распределения вероятностей и ее свойства
- •Плотность распределения вероятности и ее свойства
- •Числовые характеристики случайных величин
- •Свойства математического ожидания
- •Свойства дисперсии случайных величин
- •Числовые характеристики среднего арифметического n независимых случайных величин
- •Надёжность: основные понятия и определения
- •Основные понятия
- •Показатели надёжности
- •Показатели надежности – количественные и комплексные.
- •Основные показатели безотказности объектов Вероятность безотказной работы
- •Средняя наработка до отказа
- •Интенсивность отказов
- •Средняя наработка на отказ
- •Параметр потока отказов
- •Основные показатели долговечности Средний срок службы (математическое ожидание срока службы)
- •Средний ресурс (математическое ожидание ресурса)
- •Основные показатели ремонтопригодности
- •Среднее время восстановления
- •Интенсивность восстановления
- •Комплексные показатели надежности Коэффициент готовности
- •Коэффициент оперативной готовности
- •Коэффициент технического использования
- •Основные математические модели, наиболее часто используемые в расчётах надёжности. Распределение Вейбулла
- •Экспоненциальное распределение
- •Распределение Рэлея
- •Нормальное распределение (распределение Гаусса)
- •Примеры использования законов распределения в расчетах надежности
- •Определение показателей надежности при экспоненциальном законе распределения
- •Определение показателей надежности при распределении Рэлея
- •Определение показателей схемы при распределении Гаусса
- •Определение показателей надежности неремонтируемого объекта по опытным данным
- •Надёжность невосстанавливаемой системы при основном соединении элементов Определение вероятности безотказной работы и средней наработки до отказа
- •Пример расчета надежности системы, собранной по основной схеме
- •Порядок решения задач надёжности. Исходные положения
- •Методы расчета надежности
- •Надёжность невосстанавливаемых резервированных систем
- •Общее резервирование с постоянно включенным резервом и с целой кратностью
- •Надежность системы с нагруженным дублированием
- •Общее резервирование замещением
- •Надежность системы при раздельном резервировании и с целой кратностью по всем элементам
- •Смешанное резервирование неремонтируемых систем
- •Надёжность восстанавливаемых систем
- •Надежность восстанавливаемой одноэлементной системы
- •Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами
- •Надежность восстанавливаемой дублированной системы
- •Надежность восстанавливаемой системы при различных способах резервирования элементов
Свойства математического ожидания
Свойство 1. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
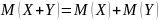
Свойство 2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

Свойство 3. Математическое ожидание постоянной величины равно самой постоянной:
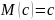
Свойство 4. Постоянный множитель случайной величины можно вынести за знак математического ожидания:
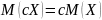
Свойство 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
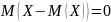
Пример 3. Найти математическое ожидание количества бракованных изделий в выборке из шести изделий, если случайная величина X (количество бракованных изделий) задана рядом распределения.
|
0 |
1 |
2 |
3 |
4 |
5 |
|
0.2373 |
0.3955 |
0.2637 |
0.0879 |
0.01460 |
0.0010 |
Решение. По формуле (4.1) находим
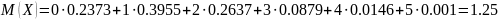
Модой
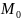 дискретной случайной величины
называется наиболее вероятное ее
значение.
дискретной случайной величины
называется наиболее вероятное ее
значение.
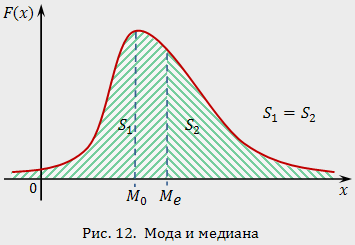
Модой непрерывной случайной величины называется такое ее значение, которому соответствует наибольшее значение плотности распределения. Геометрически моду интерпретируют как абсциссу точки глобального максимума кривой распределения (рис. 12).
С
помощью дисперсии и среднеквадратического
отклонения можно судить о рассеивании
случайной величины вокруг математического
ожидания. В качестве меры рассеивания
случайной величины используют
математическое ожидание квадрата
отклонения случайной величины от ее
математического ожидания, которое
называют дисперсией
случайной величины
и обозначают
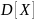 :
:
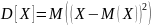
Для дискретной случайной величины дисперсия равна сумме произведений квадратов отклонений значений случайной величины от ее математического ожидания на соответствующие вероятности:
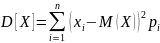
Для непрерывной случайной величины, закон распределения которой задан плотностью распределения вероятности , дисперсия
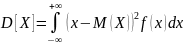
Размерность дисперсии равна квадрату размерности случайной величины и поэтому ее нельзя интерпретировать геометрически. Этих недостатков лишено среднее квадратическое отклонение случайной величины, которое вычисляется по формуле

Свойства дисперсии случайных величин
Свойство 1. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
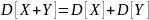
Свойство 2. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
|
(4.3) |
Свойство 3. Дисперсия постоянной величины равна нулю:
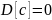
Свойство 4. Постоянный множитель случайной величины, можно выносить за знак дисперсии, предварительно возведя его в квадрат:
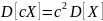
Пример 4. Вычислить дисперсию количества бракованных изделий для распределения примера 3.
Решение. По определению дисперсии
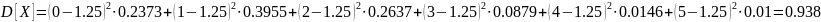
Числовые характеристики среднего арифметического n независимых случайных величин
Пусть
— значения случайной величины
,
полученные при
независимых испытаниях. Математическое
ожидание случайной величины равно
,
а ее дисперсия
.
Эти значения можно рассматривать как
независимые случайные величины
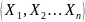 с одинаковыми математическими ожиданиями
и дисперсиями:
с одинаковыми математическими ожиданиями
и дисперсиями:

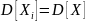

Среднее арифметическое этих случайных величин
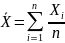
Используя свойства математического ожидания и дисперсии случайной величины, можно записать:
|
(4.4) |
|
(4.5) |