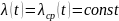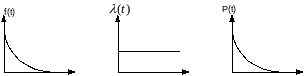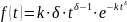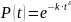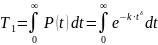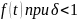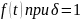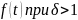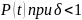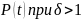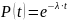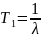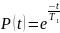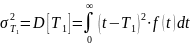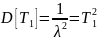Основные математические модели, наиболее часто используемые в расчётах надёжности. Распределение Вейбулла

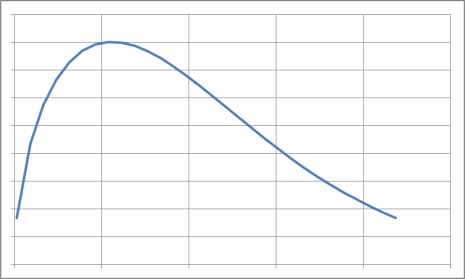
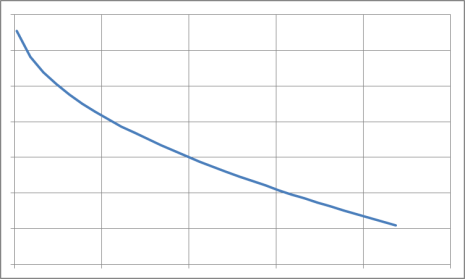
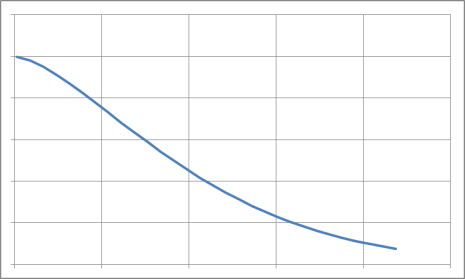
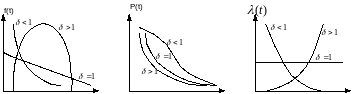
Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени (рис. 3.1), соответствующих трем периодам жизни этих устройств.

Нетрудно увидеть, что этот рисунок аналогичен рис. 2.3, так как график функции соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла. Согласно этому распределению плотность вероятности отказов равна:

(3.1)

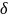– параметр формы (определяется подбором в результате обработки экспериментальных данных, );

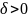– параметр масштаба.

Интенсивность отказов определяется по выражению

(3.2)

Посчитаем вероятность безотказной работы:

(3.3)

Среднюю наработку до отказа можно вычислить по формуле:

(3.4)

Отметим, что при параметре 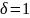распределение Вейбулла переходит в экспоненциальное, а при 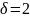– в распределение Рэлея.

Период нормальной эксплуатации можно представить распределением Вейбулла с параметром . При этом интенсивность отказов будет постоянной.

Период приработки можно представить распределением Вейбулла с параметром 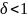. При этом интенсивность отказов монотонно убывает.

Период износа можно представить распределением Вейбулла с параметром 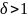. При этом интенсивность отказов монотонно возрастает.

Таким образом, путем подбора параметра можно получить, на каждом из трех участков, такую теоретическую кривую , которая достаточно близко совпадает с экспериментальной кривой, и тогда расчет требуемых показателей надежности можно производить на основе известной закономерности.

Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме.

Экспоненциальное распределение

Как было отмечено в предыдущем разделе, экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы . Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра 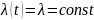. Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:

(3.5)

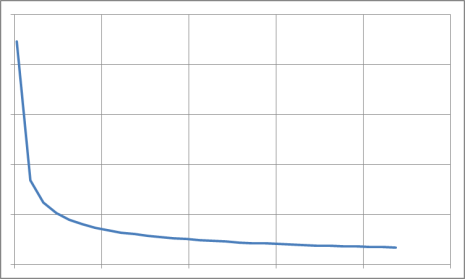
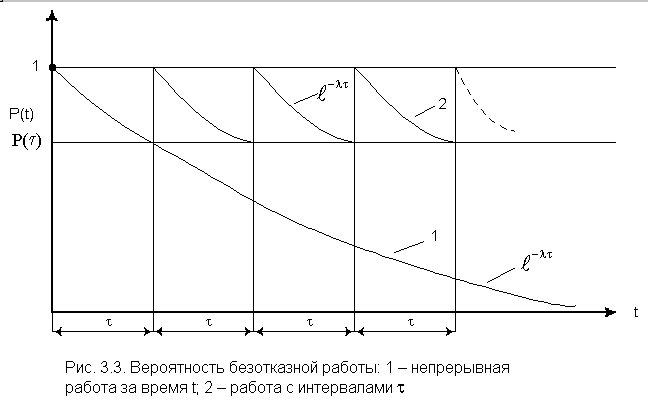
Вычислим среднее время безотказной работы при экспоненциальном законе распределения:

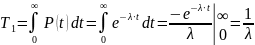
(3.6)

Заменив в выражении (3.5) величину величиной 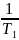, получим

(3.7)

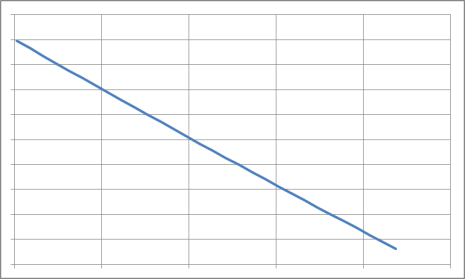
Таким образом, зная среднее время безотказной работы (или постоянную интенсивность отказов ), можно в случае экспоненциального распределения найти вероятность безотказной работы для интервала времени от момента включения объекта до любого заданного момента .

Отметим, что вероятность безотказной работы на интервале, превышающем среднее время , при экспоненциальном распределении будет менее 0,368:

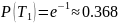
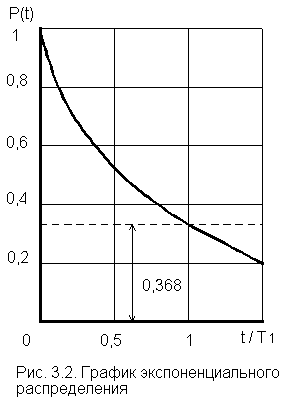
Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше , то есть интервал времени, на котором допустимо пользование экспоненциальной моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного для этой модели. Это легко обосновать, воспользовавшись дисперсией времени безотказной работы. Как известно, если для случайной величины задана плотность вероятности и определено среднее значение (математическое ожидание) , то дисперсия времени безотказной работы находится по выражению:

(3.8)

и для экспоненциального распределения, соответственно, дисперсия равна:

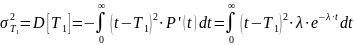
Проинтегрируем несколько раз по частям:

=

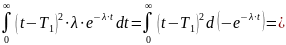
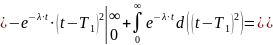
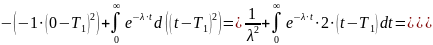
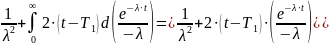
Таким образом, получаем, что

(3.10)

А, значит, наиболее вероятные значения наработки, группирующиеся в окрестности , лежат в диапазоне 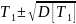= 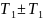, то есть в диапазоне от до 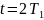. Как видим, объект может отработать и малый отрезок времени и время , сохранив 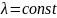. Но вероятность безотказной работы при крайне низка:

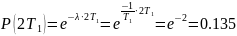
Важно отметить, что если объект отработал предположим, время 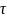без отказа, сохранив , то дальнейшее распределение времени безотказной работы будет таким, как в момент первого включения .

Таким образом, отключение работоспособного объекта в точке  и новое его включение на такой же интервал множество раз приведет к пилообразной кривой 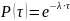 (см. рис. 3.3).

Другие распределения не имеют указанного свойства. Из рассмотренного следует на первый взгляд парадоксальный вывод: поскольку за все время t устройство не стареет (не меняет своих свойств), то нецелесообразно проводить профилактику или замену устройств для предупреждения внезапных отказов, подчиняющихся экспоненциальному закону. Конечно, никакой парадоксальности этот вывод не содержит, так как предположение об экспоненциальном распределении интервала безотказной работы означает, что устройство не стареет. С другой стороны, очевидно, что чем больше время, на которое включается устройство, тем больше всевозможных случайных причин, которые могут вызвать отказ устройства. Это весьма важно для эксплуатации устройств, когда приходится выбирать интервалы, через которые следует производить профилактические работы с тем, чтобы сохранить высокую надежность работы устройства.

Модель экспоненциального распределения часто используется для априорного анализа, так как позволяет не очень сложными расчетами получить простые соотношения для различных вариантов создаваемой системы. На стадии апостериорного анализа (опытных данных) должна проводиться проверка соответствия экспоненциальной модели результатам испытаний. В частности, если при обработке результатов испытаний окажется, что , то это является доказательством того факта, что анализируемая зависимость представляет собой экспоненциальный закон.

На практике часто бывает, что , однако, и в этом случае его можно применять для ограниченных отрезков времени. Это допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов без большой ошибки можно заменить средним значением: