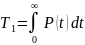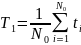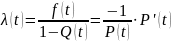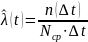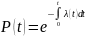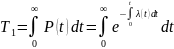- •Основные понятия теории вероятностей. События
- •Классификация событий.
- •Операции над событиями.
- •Классическое определение вероятности случайного события
- •Статистическое определение вероятности
- •Геометрическая вероятность
- •Аксиомы теории вероятностей.
- •Зависимые и независимые случайные события. Основные формулы сложения и умножения вероятностей
- •Теоремы сложения вероятностей
- •Зависимые и независимые события. Условная вероятность.
- •Формулы умножения вероятностей
- •Формула полной вероятности
- •Одномерные случайные величины
- •Понятие случайной величины
- •Законы распределения случайной величины
- •Функция распределения вероятностей и ее свойства
- •Плотность распределения вероятности и ее свойства
- •Числовые характеристики случайных величин
- •Свойства математического ожидания
- •Свойства дисперсии случайных величин
- •Числовые характеристики среднего арифметического n независимых случайных величин
- •Надёжность: основные понятия и определения
- •Основные понятия
- •Показатели надёжности
- •Показатели надежности – количественные и комплексные.
- •Основные показатели безотказности объектов Вероятность безотказной работы
- •Средняя наработка до отказа
- •Интенсивность отказов
- •Средняя наработка на отказ
- •Параметр потока отказов
- •Основные показатели долговечности Средний срок службы (математическое ожидание срока службы)
- •Средний ресурс (математическое ожидание ресурса)
- •Основные показатели ремонтопригодности
- •Среднее время восстановления
- •Интенсивность восстановления
- •Комплексные показатели надежности Коэффициент готовности
- •Коэффициент оперативной готовности
- •Коэффициент технического использования
- •Основные математические модели, наиболее часто используемые в расчётах надёжности. Распределение Вейбулла
- •Экспоненциальное распределение
- •Распределение Рэлея
- •Нормальное распределение (распределение Гаусса)
- •Примеры использования законов распределения в расчетах надежности
- •Определение показателей надежности при экспоненциальном законе распределения
- •Определение показателей надежности при распределении Рэлея
- •Определение показателей схемы при распределении Гаусса
- •Определение показателей надежности неремонтируемого объекта по опытным данным
- •Надёжность невосстанавливаемой системы при основном соединении элементов Определение вероятности безотказной работы и средней наработки до отказа
- •Пример расчета надежности системы, собранной по основной схеме
- •Порядок решения задач надёжности. Исходные положения
- •Методы расчета надежности
- •Надёжность невосстанавливаемых резервированных систем
- •Общее резервирование с постоянно включенным резервом и с целой кратностью
- •Надежность системы с нагруженным дублированием
- •Общее резервирование замещением
- •Надежность системы при раздельном резервировании и с целой кратностью по всем элементам
- •Смешанное резервирование неремонтируемых систем
- •Надёжность восстанавливаемых систем
- •Надежность восстанавливаемой одноэлементной системы
- •Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами
- •Надежность восстанавливаемой дублированной системы
- •Надежность восстанавливаемой системы при различных способах резервирования элементов
Средняя наработка до отказа
Средней
наработкой до отказа
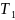 называется среднее время работы до
отказа, т.е. математическое ожидание
наработки объекта до первого отказа.
называется среднее время работы до
отказа, т.е. математическое ожидание
наработки объекта до первого отказа.
Вероятностное определение средней наработки до отказа выражается так:
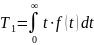
Используя известную связь между , запишем
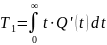
Зная, что:
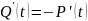
Получим:
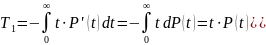
Т.к. мы исследуем реальные объекты, то логично предположить, что начиная с какого-то момента времени вероятность безотказной работы системы будет равна 0, а, значит и
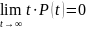
Учитывая, что
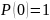
Получаем:
|
(2.6) |
Таким образом, средняя наработка до отказа равна площади, образованной кривой вероятности безотказной работы и осями координат. Статистическая оценка для средней наработки до отказа определяется по формуле:
|
(2.7) |
Где
- число работоспособных однотипных
невосстанавливаемых объектов при
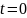 (в начале испытания);
(в начале испытания);
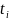 – наработка до отказа -го объекта.
– наработка до отказа -го объекта.
Отметим, что, как и в случае с определением , средняя наработка до отказа может оцениваться не только в часах (годах), но и в циклах, километрах пробега и другими аргументами.
Интенсивность отказов
Интенсивность отказов - это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не наступил. Из вероятностного определения следует, что
|
(2.8) |
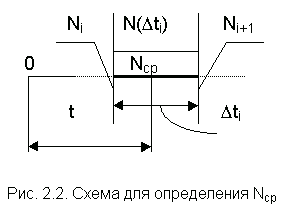
Статистическая оценка интенсивности отказов имеет вид :
|
(2.9) |
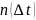 – число
отказов однотипных объектов на интервале
– число
отказов однотипных объектов на интервале
 ,
для которого определяется
,
для которого определяется
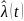 .
.
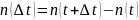
– число отказов к моменту времени .
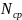 – среднее
число работоспособных объектов на
интервале
.
– среднее
число работоспособных объектов на
интервале
.
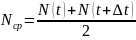
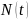 – число
работоспособных объектов в момент
времени
.
– число
работоспособных объектов в момент
времени
.
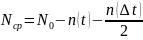
Где – число объектов, поставленных на испытания.
Посмотрим,
что получится, если устремить
к нулю (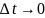 ).
).
Умножим числитель и знаменатель в формуле (2.9) на .
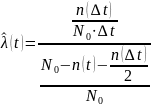
Перейдём к пределу. Учтём, что:

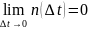
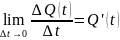
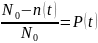
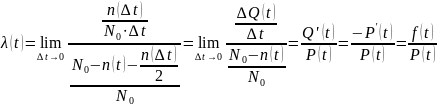
Таким образом, мы получили из статистической оценки (2.9) формулу (2.8) для интенсивности потока отказов.
Проинтегрируем выражение:
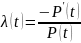
Получим:
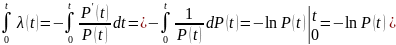
Отсюда:
|
(2.11) |
Выражение
(2.11) показывает связь
 и
.
Из этой связи ясно видно, что по
аналитически заданной функции
легко определить
и
:
и
.
Из этой связи ясно видно, что по
аналитически заданной функции
легко определить
и
:
|
(2.12) |
Если при статистической оценке время эксперимента разбить на достаточно большое количество одинаковых интервалов за длительный срок, то результатом обработки опытных данных будет график, изображенный на рис. 2.3.
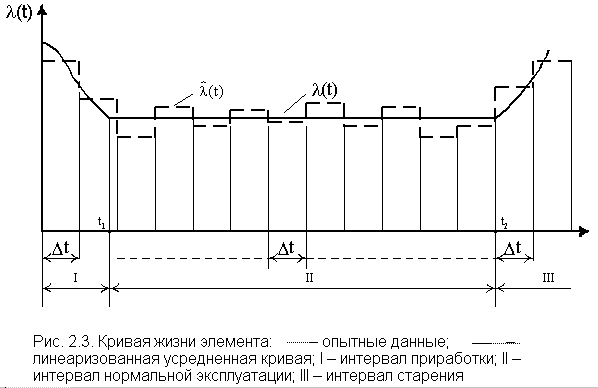
Как
показывают многочисленные данные
анализа надежности большинства объектов
техники, в том числе и электроустановок,
линеаризованная обобщенная зависимость
представляет собой сложную кривую с
тремя характерными интервалами (I, II,
III). На интервале II
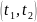
 .
Этот интервал может составлять более
10 лет, он связан с нормальной эксплуатацией
объектов. Интервал I
.
Этот интервал может составлять более
10 лет, он связан с нормальной эксплуатацией
объектов. Интервал I
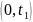 часто называют периодом приработки
элементов. Он может увеличиваться или
уменьшаться в зависимости от уровня
организации отбраковки элементов на
заводе-изготовителе, где элементы с
внутренними дефектами своевременно
изымаются из партии выпускаемой
продукции. Величина интенсивности
отказов на этом интервале во многом
зависит от качества сборки схем сложных
устройств, соблюдения требований монтажа
и т.п. Включение под нагрузку собранных
схем приводит к быстрому "выжиганию"
дефектных элементов и по истечении
некоторого времени t1
в схеме остаются только исправные
элементы, и их эксплуатация связана c
.
На интервале III
часто называют периодом приработки
элементов. Он может увеличиваться или
уменьшаться в зависимости от уровня
организации отбраковки элементов на
заводе-изготовителе, где элементы с
внутренними дефектами своевременно
изымаются из партии выпускаемой
продукции. Величина интенсивности
отказов на этом интервале во многом
зависит от качества сборки схем сложных
устройств, соблюдения требований монтажа
и т.п. Включение под нагрузку собранных
схем приводит к быстрому "выжиганию"
дефектных элементов и по истечении
некоторого времени t1
в схеме остаются только исправные
элементы, и их эксплуатация связана c
.
На интервале III
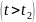 по причинам, обусловленным естественными
процессами старения, изнашивания,
коррозии и т.д., интенсивность отказов
резко возрастает, увеличивается число
деградационных отказов. Для того, чтобы
обеспечить
необходимо заменить неремонтируемые
элементы на исправные новые или
работоспособные, отработавшие время
по причинам, обусловленным естественными
процессами старения, изнашивания,
коррозии и т.д., интенсивность отказов
резко возрастает, увеличивается число
деградационных отказов. Для того, чтобы
обеспечить
необходимо заменить неремонтируемые
элементы на исправные новые или
работоспособные, отработавшие время
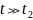 .
Интервал
соответствует экспоненциальной модели
распределения вероятности безотказной
работы. Эта модель подробно проанализирована
в подразделе 3.2. Здесь же отметим, что
при
значительно упрощается расчет надежности
и
.
Интервал
соответствует экспоненциальной модели
распределения вероятности безотказной
работы. Эта модель подробно проанализирована
в подразделе 3.2. Здесь же отметим, что
при
значительно упрощается расчет надежности
и
 наиболее часто используется как исходный
показатель надежности элемента.
наиболее часто используется как исходный
показатель надежности элемента.