9. Матричный метод решения систем линейных уравнений

Пусть система имеет квадратную матрицу А, определитель Δ которой отличен от нуля. Тогда система имеет единственное решение , которое может быть найдено по формуле .

Отметим, что А^-1 существует, т.к. определитель Δ матрицы А не равен нулю.

Пример 2.3.13. Решить матричным методом систему уравнений

Решение.

Из примера 12 имеем

,

и, следовательно,

т.е.

10. Правило Крамера

Пусть система линейных уравнений имеет квадратную матрицу А, определитель Δ которой отличен от нуля. Тогда система имеет единственное решение 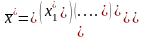, которое может быть найдено по формулам

Здесь Δ_j (j=1, ...., n) – определители матриц, которые получаются из матрицы А заменой в ней j-ого столбца на столбец свободных членов.

Пример 2.3.14. Решить систему линейных уравнений

Из примера 12 имеем

Далее

Далее имеем

11. Метод Гаусса

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений:

(2.3.1)

приводится к равносильной системе ступенчатого (или треугольного) вида:

, (2.3.2)

из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Под элементарными операциями понимаются следующие операции:

• перестановка строк;

• умножение строки на число, отличное от нуля;

• сложение строки матрицы с другой строкой, умноженной на отличное от нуля число.

Переход от системы (2.3.1.) к равносильной ей системе (2.3.2.) называется прямым ходом метода Гаусса, а нахождение переменных из системы (2.3.2.) – обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Матрица вида называется расширенной матрицей системы (2.3.1.), так как в нее, кроме матрицы системы (2.3.1.), дополнительно включен столбец свободных членов.

Пример 2.3.15. Решить систему линейных уравнений

Решение: Расширенная матрица имеет вид:

.

Шаг1. Так как а₁₁≠0, то умножая вторую, третью и четвертую строку строки матрицы на числа (-2), (-3), (-2) и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную х₁ из всех строк, начиная со второй. Заметив, что в новой матрице элемент а₂₂=0, поменяем местами вторую и третьи строки:

Шаг 2. Так как теперь а₂₂=-4≠0, то умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную х₂ из всех строк, начиная с третьей:

Шаг 3. Учитывая, что а₃₃=-8≠0, умножаем третью строку на 13,5/8=27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную х₃. Получим (см. последнюю матрицу) систему уравнений:

,

откуда, используя обратный ход метода Гаусса, найдем из четвертого уравнения х₄=-2; из третьего из второго: 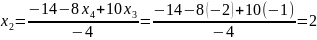и их первого уравнения: , т.е. решение системы: (1; 2; -1;2).

12. Решение слу с использованием табличного процессора ms Excel

Рассмотрены основные функции рабочего листа для работы с матрицами и приведены алгоритмы решения СЛУ матричным методом и методами Гаусса и Крамера в MS Excel.