3. Теоремы сложения и умножения вероятностей

Зная вероятности одних событий можно вычислить вероятности других событий, если они связаны между собой. Теорема сложения вероятностей позволяет определить вероятность появления одного из нескольких случайных событий.

Теорема. Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий:

.

Доказательство. Пусть n - общее число равновозможных несовместных элементарных исходов, m₁ - число исходов благоприятствующих событию А, тm₂- число исходов благоприятствующих событию В. Так как А и В несовместные события, то событию А+В будет благоприятствовать m₁+m₂ исходов. Тогда, согласно классическому определению вероятности

.

Расширяя это доказательство на n событий можно доказать следующую теорему.

Теорема. Вероятность суммы конечного числа попарно несовместных событий А₁, А₂, ..., А_n равна сумме вероятностей этих событий, т.е.

.

Из этой теоремы можно вывести два следствия:

Следствие 1. Если события А₁, А₂, ..., А_n образуют полную группу, то сумма их вероятностей равна единице, т.е.

.

Доказательство. Если события А₁, А₂, ..., А_n образуют полную группу, то наступление хотя бы одного из них есть событие достоверное. Следовательно,

; и

.

Следствие 2. Сумма вероятностей противоположных событий равна единице, т.е.

.

Доказательство. Противоположные события несовместны и образуют полную группу, а сумма вероятностей таких событий равна 1.

Пример 2.5.10. Из колоды вытаскивают карту. Найти вероятность того, что будет вытащена карта красной масти.

Решение:

Событие А – вытащена карта бубновой масти, вероятность этого события Р(А) = 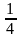. Событие В- вытащена карта червовой масти, вероятность этого события Р(В) = . События несовместные, поэтому

Ответ: .

Пример 2.5.11. На полке находится 10 книг, расставленных в произвольном порядке. Из них три книги по теории вероятностей, три – по математическому анализу и четыре – по линейной алгебре. Студент случайным образом достает одну книгу. Какова вероятность того, что он возьмет книгу по теории вероятностей или по линейной алгебре?

Решение:

Событие А – студент взял книгу по теории вероятностей, вероятность .

Событие В – студент взял книгу по математическому анализу, .

Событие С – студент взял книгу по линейной алгебре, .

Тогда .

Ответ: .

В том случае, если события А и В являются совместными, то справедлива следующая теорема.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т.е.

.

Доказательство. Пусть для полной группы событий имеющих n исходов, m₁ исходов благоприятствуют событию А, m₂- событию В, а l исходов благоприятствуют как событию А, так и событию В, тогда

; ; .

Так как событие А + В состоит в том, что произошло событие А, либо событие В, либо событие А и В. Поэтому ему будет благоприятствовать m1+m2-l исходов.

Следовательно,

.

Пример 2.5.12. Вероятность попадания в мишень одного стрелка равна 0,65, а второго 0,6. Определить вероятность поражения ми­шени при одновременных выстрелах двух стрелков.

Решение:

Так как при стрельбе возможно попадание в мишень двумя стрелками, то эти события совместные, следовательно,

.

Ответ: 0,86.

Событие А называется независимым от события В, если вероятность осуществления события А не зависит от того произошло событие В или нет.

Например, при повторении бросания игральной кости вероятность выпадения цифры 1 (событие А) не зависит от появления или не появления цифры 1 при первом бросании кости (событие В).

Событие А называется зависимым от события В, если его вероятность меняется в зависимости от того, произошло событие В или нет.

Например, если в урне находятся черные и белые шары, то вероятность повторного появления черного шара (событие А) будет зависеть от того, какой шар вынули первый раз.

В случае зависимых событий А и В вводится понятие условной вероятности, под которой понимается вероятность события А при условии, что событие В произошло. Обозначается Р(А/В).

Пример 2.5.13. В урне находится 10 шаров: 3 белых и 7 черных. Первым был вынут черный шар, найти вероятность того, что второй шар будет черным.

Решение:

Вероятность появления черного шара первый раз (событие В) равно Р(В) =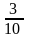 ; а вероятность появления его второй раз (событие А), при условии, что событие В произошло, равно Р(А/В) = , т.к. в урне осталось 9 шаров, из них 2 черных.

Ответ: .

Рассмотрим закон умножения вероятностей для независимых событий.

Теорема. Вероятность произведения 2 независимых событий А и В равна произведению вероятностей этих событий:

.

Этот закон справедлив и для n независимых событий:

.

Пример 2.5.14. Контролер проверяет изделия на соответствие стандарту. Известно, что вероятность соответствия стандарту изделий равна 0,9. Какова вероятность того, что из двух проверенных изделий оба будут стандартными, если события появления стандартных изделий независимы?

Решение:

А₁ – событие, состоящее в том, что первое изделие стандартно.

А₂ - событие, состоящее в том, что второе изделие стандартно.

Так как события А₁ и А₂ независимы, то по формуле умножения вероятностей независимых событий имеем:

.

Ответ: 0,81.

Теорема. Вероятность произведения двух зависимых событий А и В равна произведению одного из них на условную вероятность второго, вычисленную при условии, что первое событие осуществилось:

.

Формула умножения вероятностей может быть обобщена на случай n событий А₁, А₂,..., А_n:

.

Причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие про­изошли.

Пример 2.5.15. В группе из 20 человек, 5 студентов не подготовили задание. Какова вероятность того, что два первых студента, вызванные наугад, будут не готовы к ответу.

Решение:

Вероятность того, что первый студент не готов к ответу Р(А) = 5/20, вероятность того, что и второй студент также не подготовлен, как и первый, Р(В/А) = 4/19, тогда для ответа на вопрос воспользуемся формулой:

.

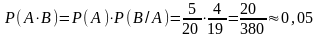Ответ: 0,05.

События А₁, А₂,..., А_n называются независимыми в совокупности, если каждое из этих событий и событие, равное произведению любого числа остальных событий, независимы.

Теорема. Вероятность появления хотя бы одного из событий А₁, А₂,..., А_n, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий А₁, А₂,..., А_n, т.e.

.

Пример 2.5.16. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0, 75, для второго – 0,8, для третьего – 0,9. Определить вероятность того, что в цель попадет хотя бы один стрелок.

Решение:

Событие А – поражение цели хотя бы одним стрелком. Тогда противоположное событие обозначим . Оно наступит тогда, когда наступит событие . Тогда

.

Ответ: 0,995.

Пример 2.5.17. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один стрелок.

Решение:

Событие А₁– поражение цели первым стрелком; А₂ - поражение цели вторым стрелком. Эти события независимые.

Вероятность того, что в мишень попадает первый стрелок и не попадает второй, равна: .

Вероятность того, что попадет второй стрелок в мишень и не попадет первый, равна: .

Вероятность того, что в мишень попадет только один стрелок, равна сумме этих вероятностей (т.к. эти вероятности несовместны, то можно использовать формулу сложения вероятностей несовместных событий): .

Ответ: 0,38.