4. Характеристики положения и рассеяния статистического распределения

В разделе теории вероятностей были рассмотрены числовые характеристики случайных величин: математическое ожидание, дисперсия, среднее квадратическое отклонение. Аналогичные числовые характеристики вводятся и для вы­борочных данных. Выборочные аналоги можно определить как из результатов наблюдения, представленных в виде последовательности x₁, х₂, ..., х_n, так и предварительно сгруппированных в виде статистического распределения или гистограммы.

Аналогом основной характеристики положения математического ожидания случайной величины является выборочное среднее:

.

Кроме математического ожидания, параметрами характеризующими центр статистического распределения является медиана и мода

Для характеристики рассеяния вариант относительно своего выборочного среднего вводят характеристику, называемую выборочной дисперсией, которая является аналогом дисперсии генеральной совокупности и равна:

.

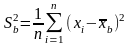Квадратный корень из выборочной дисперсии называется выборочным среднеквадратическим отклонением:

.

Иногда, для сравнения вариабельности признаков имеющих различную размерность, применяют безразмерный показатель, который называется коэффициент вариации. Этот показатель представляет процентное отношение среднего квадратического отклонения к выборочной средней:

.

Кроме рассмотренных средних величин, называемых аналитическими, в статистическом анализе применяются структурные или порядковые, средние. Из них наиболее широко применяются медиана и мода.

Медианой вариационного ряда называется значение признака, приходящегося на середину ранжированного ряда наблюдений.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов.

Пример. 2.6.2. Найти медиану распределения рабочих по тарифному разряду по данным таблицы:

Таблица 2.6.1.

Тарифный разряд xi	1	2	3	4	5	6	Ʃ
Частота (количество рабочих) ni	2	3	6	8	22	9	50

Решение: n=50 – четное, следовательно, серединных вариантов два: х₂₅=5 и х₂₆=5. Поэтому =(х₂₅+х₂₆)/2 = (5+5)/2 = 5.

При исчислении медианы интервального ряда сначала находится интервал, содержащий медиану. Медианному интервалу соответствует первый из интервалов, для которых накопленная сумма частот превышает половину общей совокупности наблюдений.

Далее определяем значение медианы по формуле:

,

где x_n – начало медианного интервала;

h – ширина медианного интервала;

n_Me – частота медианного интервала;

S_Me-1 – сумма частот интервалов, предшествующих медианному;

n – объем совокупности;

n/2 – накопленная частота до значения медианы;

n/2-S_Me-1 – частота интервала от x_n до Me, ширина которого равна Me-x_n.

Пример 2.6.3. Вычислить медиану по данным таблицы 2.6.2:

Таблица 2.6.2.

Количество баллов	Число учащихся ni	xi	xini
1-3	26	2	52
4-6	478	5	2390
7-9	369	8	2952
10-12	127	11	1397
Ʃ	1000		6791

Решение: Из таблицы имеем x_n=4, h=6∙4=2, n_Me=478, S_Me-1=26, n=1000;

Полученный результат означает, что примерно половина девятиклассников области написали контрольную работу на 6 и меньше баллов, а половина – на 6 и более баллов.

Модой вариационного ряда называется вариант, которому соответствует наибольшая частота.

Например, для вариационного ряда таблицы 2.6.1. мода =5, т.к. этому варианту соответствует наибольшая частота n_i = 22.

В случае интервальных рядов с равными интервалами за приближенное значение моды можно взять центр модального интервала, т.е. интервала с наибольшей частотой или относительной частотой. Точнее значение моды можно получить по формуле:

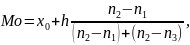
где x₀ – начальное значение модального интервала, т.е. интервала, который содержит моду;

n₂ – частота модального интервала;

n₁ – частота интервала, предшествующего модульному;

n₃ – частота интервала, следующего за модальным.

Пример 2.6.3. Вычислить моду по таблице 2.6.2.

Решение: Здесь модальным является инте рвал (4-6), т.к. он имеет наибольшую частоту: x₀ = 4, h = 2, n₂ = 478, n₁ = 26, n₃ = 369. Поэтому

1 Примечание: Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

2 Относительные и абсолютные ссылки. В зависимости от выполняемых задач в Excel можно использовать относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, или абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например, $A$2, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при их копировании, а абсолютные ссылки — нет.