7. Ввести параметры для решения злп

• В диалоговом окне указатель мышки на кнопку «Параметры». На экране появляется диалоговое окно «Параметры поиска решения» (рис. 2.4.15.).

Рис.2.4.15.

• Установите флажки в окнах «Линейная модель» (это обеспечит применение симплекс - метода) и «Неотрицательные значения».

• Указатель мышки на кнопку «ОК». На экране диалоговое окно «Поиск решения».

• Указатель мышки на кнопку «Выполнить».

Через непродолжительное время появится диалоговое окно «Результаты поиска решения» и исходная таблица с заполненными ячейками А3:В3 для значений Х_i и ячейка С3 с максимальным значением целевой функции (рис.2.4.16.).

Рис.2.4.16.

Если указать тип отчета «Устойчивость», то можно получить дополнительную информацию об оптимальном решении (Рис. 2.4.17.).

Рис. 2.4.17.

В результате решения задачи получили ответ:

Х1 = 70 - необходимо сшить женских костюмов,

Х2 = 80 - необходимо сшить мужских костюмов,

F(x) = 2300 что бы получить максимальную прибыль.

Список литературы к теме

1. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде ЕХСЕL / Практикум: Учебное пособие для вузов. - М.:ЗАО Финстатинформ, 2000.-136 с.

2. Гарнаев. Excel, VBA, Интернет.

5. Теория вероятностей

   1. Элементы комбинаторики

Комбинаторика – один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной техники, кибернетике. Комбинаторика — раздел математики, изучающий, в частности, методы решения комбинаторных задач — задач на подсчет числа различных комбинаций.

Пусть A_j (i = 1,2,...,n) — элементы конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.

Правило суммы. Если элемент А₁ может быть выбран n₁ способами, элемент А₂ — другими n₂ способами, А₃ — отличными от первых двух n₃ способами и т.д., А_k — n_k способами, отличными от первых (k—l), то выбор одного из элементов: или А₁, или A₂,...,

или А_k может быть осуществлен n₁+n₂+…+n_k способами.

Пример 2.5.1. В ящике 300 деталей. Известно, что 150 из них — 1-го сорта, 120 — 2-го, а остальные — 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?

Решение:

Деталь 1-го сорта может быть извлечена n₁=150 способами, 2-го сорта — n₂=120 способами. По правилу суммы существует n₁+n₂ = 150+120=270 способов извлечения одной детали 1-го или 2-го сорта.

Правило произведения. Если элемент А₁ может быть выбран n₁ способами, после каждого такого выбора элемент A₂ может быть выбран n₂ способами и т.д., после каждого (k—1) выбора элемент А_k может быть выбран n_k способами, то выбор всех элементов А₁, А₂,...,А_k в указанном порядке может быть осуществлен n₁n₂…n_k способами.

Пример 2.5.2. В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение:

Старостой может быть выбран любой из 30 учащихся, его заместителем — любой из оставшихся 29, а профоргом — любой из оставшихся 28 учащихся, т.е. n₁=30, n₂ =29,

n₃=28. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно n₁n₂n₃ = 30·29·28 = 24 360 способов.

Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества, отличающиеся только порядком расположения этих элементов. Такие комбинации называют перестановками из n элементов. Число перестановок из n элементов равно

,

где n! равно произведению n первых чисел натурального ряда, т.е. n!=1·2·…·n.

Замечание. 0!=1.

Пример 2.5.3. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Решение:

Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число по формуле:

, т.е. .

Ответ: 5040.

Пусть дано множество из n различных элементов. Из этого множества могут быть образованы подмножества из m элементов (0 ≤ m ≤ n). Например, из 5 элементов а, b, с, d, e могут быть отобраны комбинации по 2 элемента — ab, cd, eb, ba, се и т.д., по 3 элемента — abc, cbd, cba, ead и т.д.

Если комбинации из n элементов по m отличаются либо составом элементов, либо порядком их расположения (либо и тем и Другим), то такие комбинации называют размещениями из n элементов по m. Число размещений из n элементов по m равно

.

Пример 2.5.4. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение:

Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов как составом дисциплин, так и порядком их следования (или и тем

и другим), т.е. является размещением из 11 элементов по 5. Число вариантов расписаний, т.е. число размещений из 11 по 5, находим по формуле

,

т.е. .

Ответ: 55440.

Если комбинации из n элементов по m отличаются только составом элементов, то их называют сочетаниями из n элементов по m. Число сочетаний из n элементов по m равно

.

Пример 2.5.5. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение:

Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 16 элементов по 2. Их число

находим по формуле:

, т.е. .

Ответ: 120.

Если в размещениях (сочетаниях) из n элементов по m некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения (сочетания) называют размещениями (сочетаниями) с повторениями из n элементов по m.

Например, из 5 элементов а, b, с, d, e по 3 размещениями с повторениями будут abc, cba, bed, cdb, bbe, ebb, beb, ddd и т.д., сочетаниями с повторениями будут abc, bed, bbe, ddd и т.д.

Число размещений с повторениями из n элементов по m равно

,

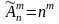а число сочетаний с повторениями из n элементов по m равно

.

Пример 2.5.6. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены: а) различные

призы; б) одинаковые призы?

Решение:

а) Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом фильмов, так и их

порядком по номинациям (или и тем и другим), причем одни и те же фильмы могут повторяться несколько раз (любой фильм может получить призы как по одной, так и по нескольким, включая все пять, номинациям.), т.е. представляет размещение с повторениями из 10 элементов по 5. Их число найдем по формуле:

, т.е .

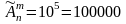б) Если по каждой номинации установлены одинаковые призы, то порядок следования фильмов в комбинации 5 призеров значения не имеет, и число вариантов распределения призов представляет собой число сочетаний с повторениями из 10 элементов по 5, определяемое по формуле:

, т.е. .

Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется n₁ раз, 2-й элемент — n₂ раз, k-й элемент — n_k раз, причем n₁+n₂+…+n_k=n, то такие перестановки называют перестановками с повторениями из n элементов. Число перестановок с повторениями из n элементов равно

.

Пример 2.5.7. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 — по 2 раза?

Решение:

Каждое семизначное число отличается от другого порядком следования цифр (причем n1=3, n2=2, n3=2, а их сумма равна 7, т.е. является перестановкой с повторениями из 7 элементов. Их число найдем по формуле:

, т.е. .

Ответ: 210.