3. Основы линейной алгебры

   1. Определение матрицы

Произвольная система вещественных чисел, записанная в виде прямоугольной таблицы, содержащей m строк и n столбцов, называется матрицей размерностью m×n.

Числа, из которых состоит матрица, называются элементами матрицы.

Матрицы обозначаются большими латинскими буквами либо в круглых скобках 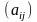, где , .

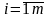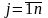Пример 2.3.1. 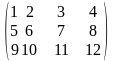- матрица, содержащая 3 строки (m = 3) и 4 столбца (n = 4).

Числа, из которых состоит матрица, называются ее элементами и обозначаются алыми латинскими буквами с двумя индексами:

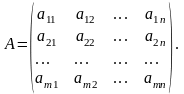
Индексы i и j элемента а_ij указывают место нахождения этого элемента в матрице А: первый индекс i – номер строки, а второй j – номер столбца, на пересечении которых расположен элемент а_ij.

Если матрица имеет одинаковое количество строк и столбцов (т.е. m=n), то она называется квадратной матрицей порядка n.

Матрица, состоящая из одной строки, называется вектор-строкой. Матрица, состоящая из одного столбца, называется вектор-столбец.

2. Определители второго и третьего порядков, их основные свойства

Пусть А – квадратная матрица. Тогда можно говорить об определителе этой матрицы, т.е. о некотором числе Δ, связанным с этом матрицей и вычисляемом по ее элементам.

1) Определитель матрицы первого порядка

2) Определитель матрицы второго порядка вычисляется по формуле:

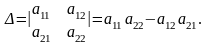
Пример 2.3.2.

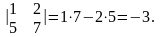
3) Определитель матрицы третьего порядка вычисляется по формуле:

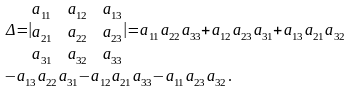
Для запоминания этой формулы существует мнемоническое правило треугольника

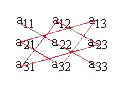
Пример 2.3.3.

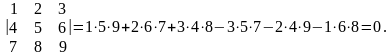
3. Миноры и их алгебраические дополнения, разложение определителя по строке (столбцу)

Минором некоторого элемента определителя называется определитель, получаемый из данного определителя вычеркиванием i-ой строки и j-ого столбца, на пересечении которых расположен этот элемент. Обозначается такой минор через M_ij.

Пример 2.3.4.

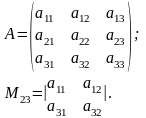
Алгебраическим дополнением элемента а_ij называется выражение Таким образом, алгебраическое дополнение по модулю совпадает с соответствующим минором, и если при этом сумма индексов i+j нечетная, то знак алгебраического дополнения противоположен знаку соответствующего минора.

Для матриц более высокого порядка (n>2)определитель вычисляется по формуле разложения определителя по первой строке:

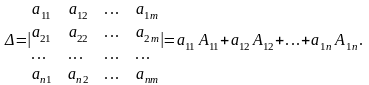
Пример 2.3.5. Вычислить определитель матрицы

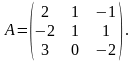
Решение.

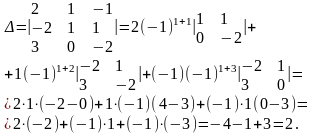
ТЕОРЕМА (разложение по i-ой строке).

Определитель n-ого порядка можно вычислять разложением по любой строке или по любому столбцу, т.е.

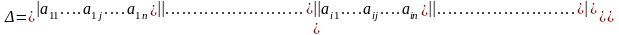(разложение по i-ой строке),

(разложение по j-му столбцу).

Пример 2.3.6. Вычислим определитель матрицы А из примера 5 разложением по 3-ей строке и по второму столбцу.

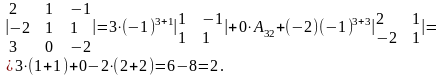
4. Свойства определителей

1. Определитель равен нулю, если

а) какая-либо его строка (или столбец) состоит из одних нулей;

б) две стоки (два столбца) определителя равны или пропорциональны.

2. Определитель не меняется:

а) при транспонировании;

б) если какой-либо его строке (или столбцу) прибавить другую строку (столбец), умноженную на произвольное число.

3. Общий множитель какой-либо строки (столбца) можно вынести за знак определителя.

4. При перестановке двух строк (двух столбцов) определитель меняет знак.

5. Определитель произведения квадратных матриц равен произведению их определителей.