Введение в теорию множеств
Приводятся начальные сведения о множествах и основные понятия подмножества, мощности. Даются возможные способы представления множеств. Рассматриваются операции над множествами, такие как объединение, пересечение, разность и дополнение
Начальные сведения о множествах
Одним из основных исходных понятий математики является понятие множества и его элементов. Основатель теории множеств Кантор дал такую трактовку: "Под множеством понимают объединение в одно общее объектов, хорошо различимых нашей интуицией или нашей мыслью".
Понятие множества, как и любое другое исходное понятие, не имеет строгого математически точного описания. Можно дать следующее определение.
Множество - это совокупность объектов, причем таких, объединенных по определенному признаку.
О множестве известно, что оно состоит из элементов. Например, множество студентов определенного университета, множество зрителей данного театра и т.п.
Как правило, элементы
множества обозначаются малыми латинскими
буквами (a,
b,
c,
…), а сами множества – заглавными (A,
B,
C,
…). Принадлежность элемента а
множеству М
обозначается так:
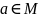(читается «а принадлежит М»). Непринадлежность
элемента b
к множеству М обозначается
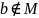(читается «b
не принадлежит М»).
Множества могут быть конечными, бесконечными и пустыми. Множество, содержащее конечное число элементов, называется конечным.
Если множество не
содержит ни одного элемента, то оно
называется пустым и обозначается
.
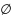Универсальным множеством U называется множество всех рассматриваемых в данной задаче элементов.
Множество А называют
подмножеством множества В (обозначается
),
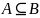если всякий элемент множества A
является элементом множества B:
(рис. 2.2.1.).
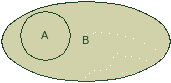
Рис. 2.2.1. Подмножество
При этом говорят,
что B
содержит А, или B
покрывает A.
Невключение подмножества C
в множество B
обозначается так:
.
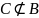Множества А и В равны
(А = В) тогда и только тогда, когда
,
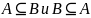т. е. элементы множеств А и В совпадают.
Множество А называется
собственным
подмножеством множества В, если
,
а
.
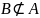Обозначается так:
.
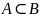Пример 2.2.1. Если B = {a, b, c, d, e, f}, A = {a, c, d}, то .
К несобственным подмножествам любого множества относятся пустое множество и данное множество.
Мощностью конечного
множества M
называется число его элементов.
Обозначается
.
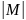Например,
.
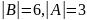Семейством или
булеаном множества M
является множество, элементами которого
являются всевозможные подмножества
множества (обозначается
).
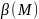Например,
M
= {a,
b,
c},
.
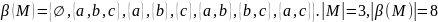В общем случае
мощность булеана
.
Способы задания множеств
Множества могут быть заданы тремя способами:
Перечислением всех элементов, входящих в множество. Таким способом можно задать только конечные множества. Обозначение – список в фигурных скобках. Например, множество натуральных чисел, являющихся делителем числа 6: N = {1, 2, 3, 6}.
Описанием характеристического свойства, которым обладают все элементы множества. Обозначается: N = {x| P(x)} или N = {x: P(x)}. Например, множество корней квадратного уравнения
можно записать следующим образом:
.
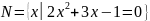Свойство P
состоит в том, что элементы являются
корнями данного квадратного уравнения.Графическим способом с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера ограничивает множество, а рамка - универсальное пространство U (рис. 2.2.2.). Заданы два множества: A = {a, b, c} и B = {b, d, e, f}. Если элементов множеств немного, то они могут на диаграмме указываться явно.
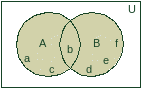
Рис. 2.2.2. Графический способ задания множеств с помощью диаграммы Эйлера-Венна