3 СистемЫ сил

Системы сил могут быть плоскими или пространственными (рис. 1.19). По расположению сил плоские и пространственные системы сил бывают: сходящимися, параллельными и произвольно расположенными.

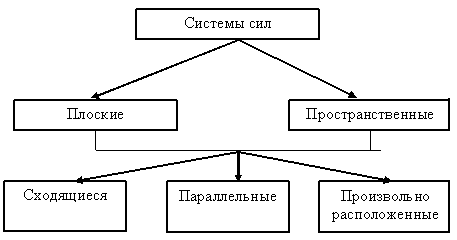
Рис. 1.19

В сходящейся системе сил линии действия всех сил пересекаются в одной точке (рис. 1.20).

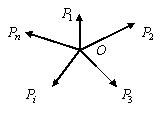
Рис. 1.20 Рис. 1.21

В параллельной системе сил линии действия сил параллельны (рис. 1.21).

В произвольно расположенной системе сил не все силы, сходящиеся или параллельные (рис. 1.22). На рис. 1.22 силы и параллельны, а сила наклонена под углом .

Рис. 1.22

Силы, приложенные к телу в какой-нибудь одной его точке (рис. 1.21, 1.22). называются сосредоточенными.

Силы, действующие на все точки данного тела или данной части тела, называются распределенными.

Распределенная нагрузка характеризуется интенсивностью q, то есть нагрузкой, приходящейся на единицу длины нагруженного отрезка, измеряется интенсивность в н/м. Равнодействующая распределенной нагрузки численно равна площади графика, занимаемого нагрузкой на чертеже и приложена к балке, проходящей через цент тяжести графика.

1. Силы, равномерно распределенные вдоль нагруженного отрезка прямой (рис. 1.23, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей , численно равной площади прямоугольника, высота которого q, а основание l.

; .

Приложена в точке С, проходящей через центр тяжести прямоугольника, т.е. делит основание АВ пополам.

2. Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 1.23, б). Равнодействующая численно равна площади треугольника АВС

;

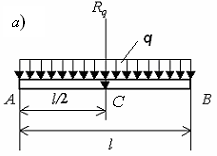
Рис. 1.23

и приложена на расстоянии от максимального значения q.

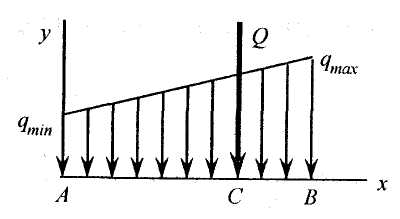
Рис. 1.24

3. Силы, распределенные вдоль отрезка прямой в виде трапеции (рис. 1.24). Равнодействующая численно равна

.

Лекция 2 система сходящихся сил

1 Проекции силы на ось и на плоскость

Взяв правую систему неподвижных осей декартовых координат х,у и z, разложим силу по правилу параллелепипеда на три составляющие силы , и , направленные параллельно этим осям (рис. 2.1).

Рис. 2.1

Силы , и называются компонентами силы по осям х, у и z.

Алгебраические значения длин направленных отрезков Аа, Аb и Ас называются проекциями силы на оси x,y и z.

Обозначив , и единичные векторы, направленные по осям х, у и z, а X,Y,Z - проекции силы на эти оси, получим

.

Но

;

поэтому

. (2.1)

Равенство (2.1) представляет собой формулу разложения силы на составляющие по осям координат.

Проекция силы на каждую координатную ось определяется произведением модуля силы на косинус угла между направлениями оси и силы:

, (2.2)

где - углы, заключенные между направлением силы и направлениями осей х,у и z.

Если известны проекции силы на три взаимно перпендикулярные оси х, у и z, то модуль и направление силы определяются по следующим формулам:

; (2.3)

(2.4)

Если рассматриваются силы, лежащие в одной плоскости, то, взяв две взаимно перпендикулярные оси х и у в этой плоскости, каждую силу можно разложить на две составляющие силы и , направленные параллельно этим осям (рис. 2.2). В этом случае Модуль и направление силы определяются по проекциям:

. (2.5)

Рис. 2.2

В формуле (2.2) угол представляет собой угол α между направлениями силы и оси x, проведенной через точку приложения силы (рис. 2.3). Этот угол отсчитывается от оси по часовой стрелке или против; он не должен превышать 180° при любом направлении силы.

Рис. 2.3

При вычислении проекции силы на ось возможны следующие частные случаи:

Проекция положительна: .

2. Проекция равна нулю: .

3. Проекция отрицательна: ,

где β - острый угол между линией действия силы и осью.

При решении задач рекомендуется вычислять абсолютное значение проекции силы как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции непосредственно по чертежу.