Если силы, действующие на систему, потенциальны, т.е. система консервативна, то обобщенная сила равна
.
Тогда уравнение (3.45) примет вид
.
(3.30)
Задача 5. Исследование механической системы с применением уравнений Лагранжа второго рода
По условию задачи № 3 определить ускорение тела 1, используя уравнение Лагранжа П рода.
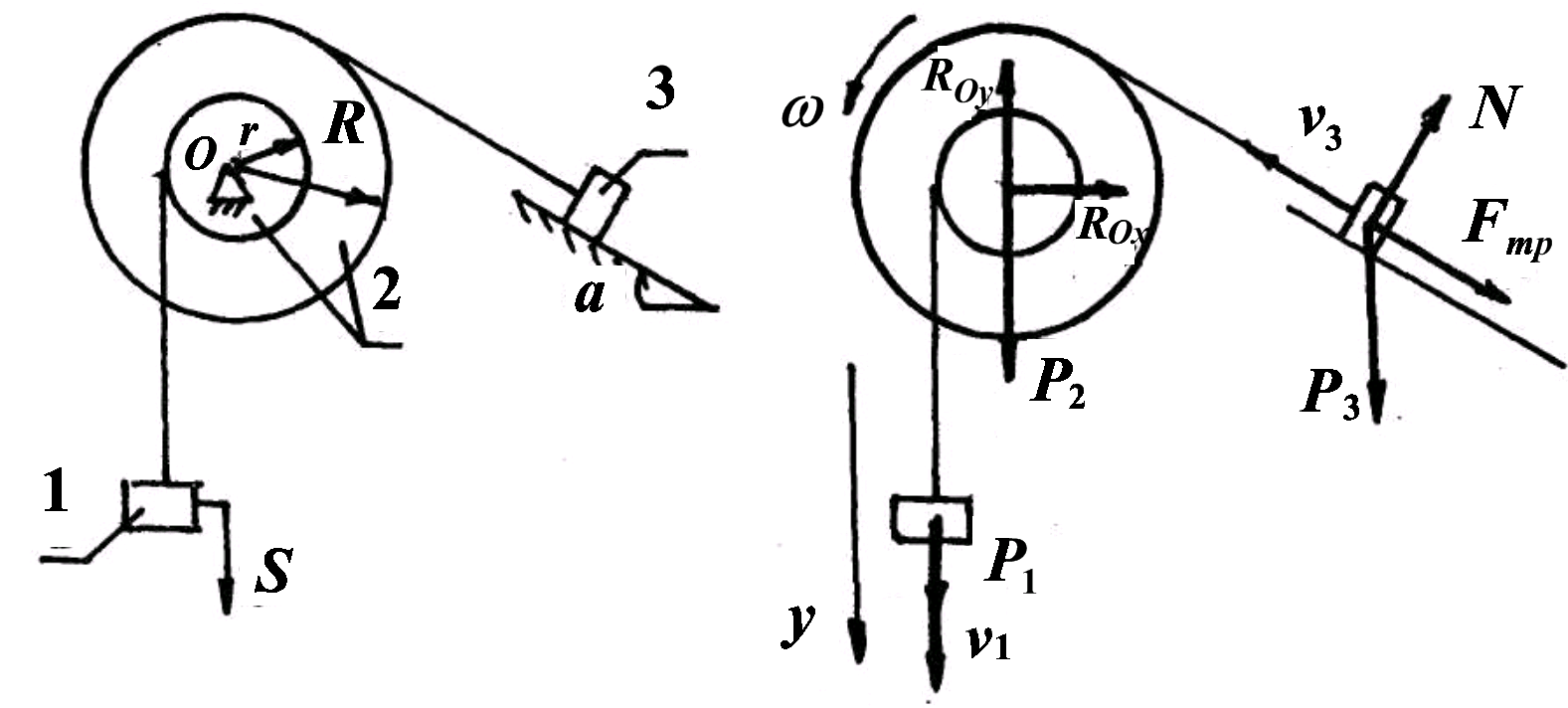
Решение.
1.
Составление расчетной схемы.. На
механическую систему действуют
активные
силы
,
,
.
Применяя
принцип освобождаемости от связей
только к внешним связям, покажем на
расчетной схеме реакции шарнирно-неподвижной
опоры
и
реакции шероховатой поверхности
и
.
Силу трения направим в сторону,
противоположную движению тела 3.
Изобразим скорости тел системы исходя из того, что тело 1 опускается.
2. Выбор теоремы.
Задачу решаем, используя дифференциальное уравнение механической системы в обобщенных координатах
.
Так как система имеет одну степень свободы, а определяем ускорение тела 1, то за обобщенную координату примем координату первого тела у
q=y.
Обобщенная
скорость, в таком случае,
.
3. Составление уравнения.
а) Определение кинетической энергии системы.
Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1,2 и 3.
.
Вычислим Q для неконсервативных сил
,
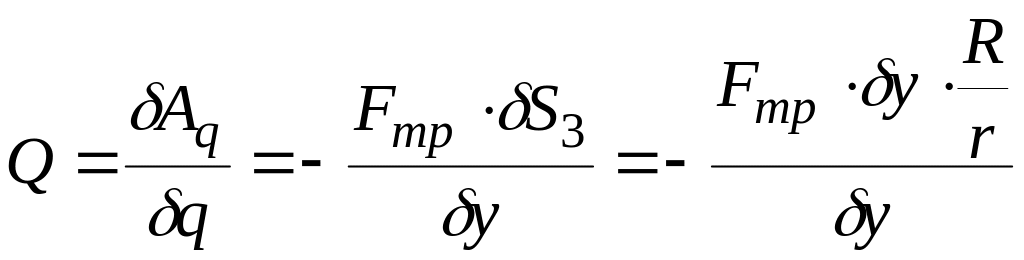то есть
.
Работа сил и на заданном приращении обобщенной координаты равна нулю, так как силы приложены к неподвижной точке. Работа нормальной реакции поверхности N также равна нулю, сила перпендикулярна направлению движения.
Подставим в обобщенную силу значения
.
или
.
в) Определение потенциальной энергии системы.
Потенциальная энергия численно равна работе потенциальных сил, действующих на систему, которую необходимо совершить, чтобы вернуть систему из отклоненного положения в положение равновесия.
.
Высота, на которую переместится точка приложения силы , равна
.
В обобщенных координатах
.
Подставляя числовые параметры, запишем
.
Подставляем значения Т, П и Q в уравнение Лагранжа П рода и преобразовываем
,
,
,
так как Т не содержит у.
.
Таким образом, запишем
,
Значение ускорения тела получили со знаком «+». Это означает, что груз опускается ускоренно.
13.3. Кинетический потенциал и циклические координаты
Уравнение (3.30) можно преобразовать путем введения функции Лагранжа L=T- П, называемой кинетическим потенциалом.
Так как
,
,
то, кинетический потенциал является функцией обобщенных координат, обобщенных скоростей и времени:
.
Потенциальная энергия является функцией только обобщенных координат и времени, а потому
.
Пользуясь этим условием, получим:
.
Подставим эти частные производные в уравнения Лагранжа (3.46):
или
.
(3.31)
Уравнения (3.31) называются уравнениями Лагранжа второго рода для консервативной системы.
Обобщенные координаты, которые не входят явно в выражение кинетического потенциала l, называются циклическими координатами.