
- •Вопрос 1. Определение производной, ее геометрический смысл.
- •Вопрос 2. Непрерывность функции, имеющей производную.
- •Вопрос 3. Производная суммы, произведения, частного.
- •Вопрос 4. Производная обратной функции.
- •Вопрос 5. Определение дифференцируемости функции. Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Вопрос 6. Дифференциал. Его геометрический смысл.
- •Вопрос 7. Производная сложной функции.
- •Вопрос 8. Производная высших порядков. Дифференциал высших порядков.
- •Вопрос 9. Дифференцирование параметрически заданной функции.
- •Вопрос 10. Теорема Ферма. Ее геометрический смысл.
- •Вопрос 11 Теорема Ролля. Ее геометрический смысл.
- •Вопрос 13. Теорема о среднем Лагранжа. Ее геометрический смысл.
- •Вопрос 14. Правило Лопиталя. Раскрытие неопределенностей. Правило Лопиталя. Случай 0/0.
- •Правило Лопиталя. Случай .
- •Раскрытие неопределенностей вида , , , , .
- •Вопрос 15. Разложение многочлена по степеням (х-а)
- •Вопрос 16. Формула Тейлора с остаточным членом в форме Лагранжа.
- •Вопрос 17. Остаточный член в форме Пеано.
- •Вопрос 18. Ряд Тейлора, его сходимость, признак сходимости.
- •Вопрос 19.
- •Экстремум функции. Необходимое условие экстремума непрерывной функции.
- •Вопрос 20. Экстремум функции. Достаточное условие экстремума непрерывной функции.
- •Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
- •Вопрос 21. Достаточное условие экстремума функции, имеющей n-ную производную.
- •Вопрос 22.
- •Выпуклость и вогнутость прямой. Точки перегиба.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Вопрос 23. Асимптоты функции.
- •Вопрос 24. Первообразная. Теорема о первообразной.
- •Вопрос 25. Неопределенный интеграл. Его свойства.
- •Вопрос 26. Метод внесения под знак дифференциала. Метод подстановки.
- •Вопрос 27. Интегрирование по частям.
- •Вопрос 28. Интегрирование рациональных дробей.
- •Вопрос 30.
- •Интегрирование тригонометрических функций.
- •Вопрос 31. Интегральная сумма, ее предел. Определение определенного интеграла.
- •Вопрос 32. Необходимое условие интегрируемости.
- •Вопрос 33. Суммы Дарбу. Их свойства.
- •Вопрос 34. Необходимое и достаточное условия интегрируемости функции.
- •Вопрос 35. Достаточное условие интегрируемости функции.
- •Вопрос 36. Свойства определенного интеграла.
- •Вопрос 37. Интеграл с переменным верхним пределом, его непрерывность.
- •Вопрос 38. Дифференцируемость интеграла с переменным верхним пределом.
- •Вопрос 39. Формула Ньютона-Лейбница.
- •Вопрос 40. Замена переменной в определенном интеграле.
- •Вопрос 41. Интегрирование по частям определенного интеграла.
- •Вопрос 42. Теорема о среднем для определенного интеграла.
- •Вопрос 43. Непрерывная и гладкая прямая, заданная параметрически. Длина этой кривой.
- •Вопрос 44. Площадь фигуры, заданной в полярной системе координат.
- •Вопрос 45. Объем тел вращения.
Вопрос 31. Интегральная сумма, ее предел. Определение определенного интеграла.
Пусть
задана функция f(x)
на отрезке
 .
Составим разбиение R:
.
Составим разбиение R:
 .
.


Это
интегральная сумма, соответствующая
разбиению R
и выбору точек
 .
.
Если
существует предел при
 интегральных
сумм
интегральных
сумм ,
и он не зависит от R
и
,
то он называется определенным
интегралом
,
и он не зависит от R
и
,
то он называется определенным
интегралом
Вопрос 32. Необходимое условие интегрируемости.
Теорема. Для того, чтобы функция f(x), определённая на отрезке [a,b], была интегрируема на нём, необходимо, чтобы она была ограничена на этом отрезке.
Доказательство. Предположим, что f(x) не ограничена на отрезке [a,b]. Тогда для каждого разбиения найдётся хотя бы один отрезок [xk−1,xk], на котором функция окажется неограниченной. Но тогда в интегральной сумме хотя бы одно слагаемое Δxkf(ξk) будет произвольно большим, и тогда последовательность интегральных сумм сходящейся быть не может. Значит, функция не интегрируема, что противоречит предполагаемому.
Вопрос 33. Суммы Дарбу. Их свойства.
Определение:
Пусть
 ограничена
на отрезке
ограничена
на отрезке
 .
Введём разбиение R
этого отрезка.
.
Введём разбиение R
этого отрезка.
R:
 ,
,
 .
.
Тогда можем составить выражения:
 -
нижняя сумма Дарбу,
-
нижняя сумма Дарбу,
 - верхняя сумма Дарбу.
- верхняя сумма Дарбу.
 ,
,
 .
.
Пусть ограничена на отрезке . Введём разбиение R этого отрезка.
R: , .
Тогда можем составить выражения:
- нижняя сумма Дарбу, - верхняя сумма Дарбу.
, .
Свойства сумм Дарбу:
1)
 ,
для одного и того же разбиения.
,
для одного и того же разбиения.
2)
Рассмотрим два разбиения в случае, когда
одно разбиение является продолжением
другого. Т.е.
 -
продолжение
-
продолжение
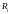 ,
если все точки
являются точками
.
,
если все точки
являются точками
.

Д обавление
точек не увеличивает
обавление
точек не увеличивает
 и не уменьшает
и не уменьшает
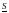 .
Пусть
получается из
добавлением одной точки.
.
Пусть
получается из
добавлением одной точки.
 ,
,
 ,
,
 ,
,
 ,
,
Заметим,
что если
 ,
то
,
то
 и
и
 .
Отсюда заключаем:
.
Отсюда заключаем:
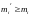 ,
,
 ,
,
 ,
,
 .
.
3)
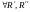
 ,
,
 ,
,
 ,
,
=>
 ,
т.е.
,
т.е.
 .
.

 -
нижний интеграл (нижняя точная сумма
Дарбу).
-
нижний интеграл (нижняя точная сумма
Дарбу).
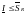 .
.
 -
верхний интеграл (верхняя точная сумма
Дарбу).
-
верхний интеграл (верхняя точная сумма
Дарбу).
 .
.
 .
.
Вопрос 34. Необходимое и достаточное условия интегрируемости функции.
Теорема:
Функция
интегрируема на отрезке
тогда и только тогда, когда
 .
.
Доказательство:
Докажем необходимость условия:
Функция интегрируема на отрезке .
Пусть
 ,
тогда
,
тогда


 ,
т.е.
,
т.е.
 .
.

т.е.
 и
и
 .
.
Далее
имеем:
 ,
т.е.
,
т.е.
 .
.
Необходимость доказана.
Докажем достаточность условия:
.
 .
.
 .
.
Докажем,
что
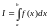 .
.
 ,
,

 ,
,
 ,
тогда
,
тогда
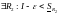 ,
т.е.
,
т.е.
 ,
,
 .
.
Достаточность доказана.
Вопрос 35. Достаточное условие интегрируемости функции.
Теорема 1:
Если функция непрерывна на , то она интегрируема на .
Доказательство:
Пусть
непрерывна на
;
тогда для разбиения R,
у которого частичные отрезки
 ,
имеет место (
,
имеет место ( ).
).

где
 есть модуль непрерывности
на
.
есть модуль непрерывности
на
.
Поэтому
 .
.
Но,
как мы знаем, для непрерывной на замкнутом
конечном отрезке
функции
 ,
поэтому для любого
,
поэтому для любого
 можно указать такое
можно указать такое
 ,
что
,
что
 .
.
В силу основной теоремы интеграл на существует.
Теорема доказана.
