31. Области устойчивости су. Метод Вышнеградского.
Поскольку при составлении математической модели делается ряд допущений, то параметры реальной системы несколько отличаются от расчетных (номинальных). Кроме того, с течением времени они могут изменяться в некотором диапазоне, но при этом свойство устойчивости должно сохраняться. Поэтому для нормальной работы система должна обладать определенным запасом устойчивости.
Рассмотрим линейную стационарную систему общего вида
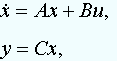
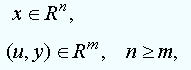
и соответствующее ей характеристическое уравнение
det(pI - A) = 0 ,
к
оторое
имеет n корней
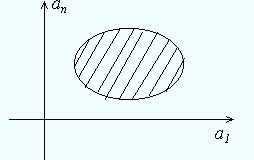
Определение: областью устойчивости по параметрам будем называть множество матриц A, для которых выполняется общее условие устойчивости, Re (A) < 0 .
На практике обычно речь идет об изменении одного - двух параметров системы.
Рис.4.19. Область устойчивости системы
Определение: критическими (граничными) будем называть такие значения матриц A, при которых система находится на границе устойчивости, Re (A) = 0.
Определение: запасом устойчивости называется диапазон значений параметра от номинального до граничного.
Примером корневых оценок качества переходного процесса в системах третьего порядка является диаграмма Вышнеградского (дана в его работе 1876г., положившей начало развитию теории автоматического регулирования).
Метод Вышнеградского позволяет строить график устойчивости и установить вид переходного процесса.
Характеристическое уравнение системы третьего порядка
,
(6)
приводится к нормированному виду
,
(7)
где
,
,
.
(8)
Параметры Вышнеградского А и В представляют, следовательно, определенные комбинации реальных параметров системы, входящих в коэффициенты характеристического уравнения.
На плоскости параметров (А, В) граница устойчивости выразится зависимостью АВ = 1
(гипербола). Область устойчивости
АВ>1
Разбивается на три подобласти (рис. 5) с различным расположением корней характеристического уравнения и соответственно – очертаний переходного процесса. При этом граничные лини CE и CF находятся приравниванием нулю дискриминанта формулы Кардана (решения кубического уравнения) в виде
,
а линия СО – из равенства вещественных частей всех корней -
A<3
В точке С(3,3) все три корня вещественные и равны – 1.
Позднее
на диаграмму Вышнеградского были
нанесены линии равных значений степени
устойчивости
и линии равных значений колебательности
.
П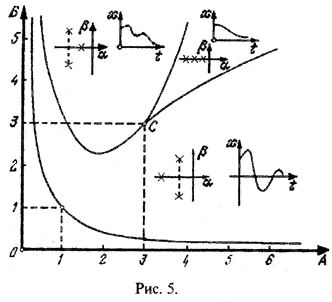
ри
определении степени
устойчивости
смещенное уравнение для нормированного
характеристического уравнения (7) будет
,
где согласно формулам (4)
,
,
.
Два условия (5) принимают соответственно вид
,
(9)
(10)
Полагая =const нанесем лини равных значений . При этом согласно уравнению (9) получим для разных конкретных значений прямые линии, а согласно уравнению (10) – кривые (рис. 6).
Д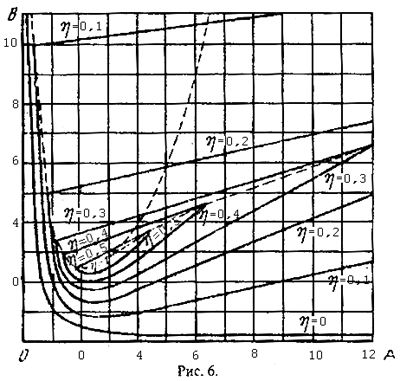
ля
определения линий равных значений
величины колебательности системы
третьего порядка (7), когда корни его
равны
,
,
имея
в виду, что
по формулам Виета, запишем
,
,
.
Исключая
и
и
обозначив
,
получим уравнение
,
(5.20)
которое
позволяет построить на поле диаграммы
Вышнеградского АВ линии равных значений
(рис. 7) в областях, где имеются комплексные
корни.
Если нам требуется в системе третьего порядка выбрать параметры так, чтобы получить заданное качество переходного процесса по показателям и , мы выбираем на рис.6 и 7 соответствующую точку. Найдя таким образом значения А и В, пользуемся затес формулами (8) для подбора параметров системы (6).
Р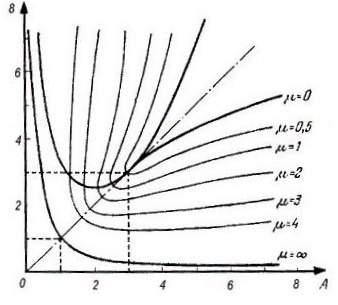
ис.7
Выводы:
Вышнеградский нашел красивое и информативное решение. Недостаток – ограничена область применения уравнениями 3-го порядка.
Исследуемые параметры системы неявным образом заняты в параметрах А и В, что требует трудоемких дополнительных расчетов.
Критерий Вышнеградского совпадает с критерием Гурвица.