17.5. Первый замечательный предел

При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел

называемый первым замечательным пределом. Читается: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю. Докажем равенство (17.11).

▼Возьмем круг радиуса 1, обозначим радианную меру угла MOB через х (см. рис. 113).

Пусть 0<х<p /2. На рисунке |АМ|=sinx, дуга MB численно равна центральному углу х, |ВС|=tgx. Очевидно, имеем S_DMOB <S_{сектораMOB}<S_D COB. На основании соответствующих формул геометрии получаем ½sinx<½x<½tgx. Разделим неравенства на ½sinx>0, получим 1<x/sinx<1/cosx или cosx<sinx/x<1. Так как limcosx=1 и lim1=1 при х–>0, то по признаку (о пределе промежуточной функции) существования пределов

Пусть  теперь  х < 0.   Имеем   

Где –x>0. Поэтому

Из равенств (17.12) и (17.13) вытекает равенство (17.11). ▲

<< Пример 17.6

Решение: Имеем неопределенность вида  . Теорема о пределе дроби неприменима. Обозначим 3х=t; тогда при х→0 и t→0, поэтому

<< Пример 17.7

17.6. Второй замечательный предел

Как известно, предел числовой последовательности

   nєN, имеет предел, равный е (см. (15.6)):

Докажем, что к числу е стремится и функция

1. Пусть х→+∞. Каждое значение х заключено между двумя положительными целыми числами: n≤х<n+1, где n=[х]— это целая часть х. Отсюда следует

Если х→+∞, то n→∞. Поэтому, согласно (17.14), имеем:

По признаку (о пределе промежуточной функции) существования пределов

 2. Пусть х→-∞. Сделаем подстановку -х= t, тогда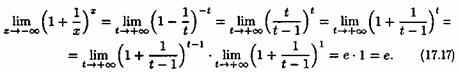 Из равенств (17.16) и (17.17) вытекает равенство (17.15).

Если в равенстве (17.15) положить 1/x=а (а→0 при х→∞), оно запишется в виде

Равенства (17.15) и (17.18) называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием е. Функция у=е^х называется экспоненциальной, употребляется также обозначение е^х=ехр(х).

<< Пример 17.8

Найти

 

Решение: Обозначим х=2t, очевидно, t→∞. при х→∞. Имеем

   

§ 18. Эквивалентные бесконечно малые функции

18. Эквивалентные бесконечно малые функции

18.1. Сравнение бесконечно малых функций

Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.

Две б.м.ф. сравниваются между собой с помощью их отношения.

Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→х_о, т. е.

 и 

1. Если  =А¹ 0 (АєR), то α и ß называются бесконечно малыми одного порядка.

2. Если,  =0, то α називатся бесконечно малой более высокого порядка , чем ß.

3. Если  =∞, то α называется бесконечно малой более низкого порядка, чем ß.

4. Если   не существует, то α и ß называются несравнимыми бесконечно малыми.

Отметим, что таковы же правила сравнения б.м.ф. при х →±∞, х →х₀±0.

<< Пример 18.1<

Сравнить порядок функций α=3х² и  ß=14х²  при х→0

Решение: При х→0 это б.м.ф. одного порядка, так как

Говорят, что б.м.ф. а и ß одного порядка стремятся к нулю с примерно одинаковой скоростью

<< Пример 18.2

Являются ли функции α=3х⁴ и ß=7х б.м.ф. одного порядка при х→0?

Решение: При х→0 функция α есть б.м.ф. более высокого порядка, чем ß, так как

В этом случае б.м.ф. α стремится к нулю быстрее, чем ß.

<< Пример 18.3

Сравнить порядок функций α=tgx и ß=х² при х→0.

Решение: Так как

то α есть б.м.ф. более низкого порядка, чем ß.

<< Пример 18.4

Можно ли сравнить функции     и ß=х при х→0?

Решение: Функции   и ß=х при х→0 являются несравнимыми б.м.ф., так как предел

не существует.