14.3. Основные характеристики функции

1. Функция у=ƒ(х), определенная на множестве D, называется четной, если " xΠD выполняются условия -хєD и ƒ(-х)=ƒ(х); нечетной, если " xєD выполняются условия -хєD и ƒ(-х)=-ƒ(х).

График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.

Например, у=х², у=√(1+х²), у=ln|х| — четные функции; а у=sinx, у=х³ — нечетные функции; у=х-1, у=√x — функции общего вида, т. е. не четные и не нечетные.

2.  Пусть функция у=ƒ(х) определена на множестве D и пусть D ₁єD. Если для любых значений х ₁;x₂єD₁аргументов из неравенства x₁<x₂ вытекает неравенство: ƒ(x ₁)<ƒ(х₂), то функция называется возрастающей на множестве D ₁; f(x₁) ≤ ƒ(х₂), то функция называется неубывающей на множестве D₁; f(x₁)>ƒ(х₂), то функция называется убывающей на множестве D₁; ƒ(х₁)≥ƒ(x₂), то функция называется невозрастающей на множестве D₁.

Например, функция, заданная графиком (см. рис. 100), убывает на интервале (-2; 1), не убывает на интервале (1; 5), возрастает на интервале (3; 5).

Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D1 называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. На рисунке (выше) функция строго монотонна на (-2; 1) и (3; 5); монотонна на (1;3).

3. Функцию у=ƒ(х), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М>0, что для всех хєD выполняется неравенство |ƒ(х)|≤М (короткая запись: у=ƒ(х), хєD, называется ограниченной на D, если  $М>0: "xєD ==>|ƒ(х)|≤М). Отсюда следует, что график ограниченной функции лежит между прямыми у=-М и у=М (см. рис. 101).

4. Функция у=ƒ(х), определенная на множестве D, называется периодической на этом множестве, если существует такое число Т>0, что при каждом хєD значение (х+Т)єD и ƒ(х+Т)=ƒ(х). При этом число Т называется периодом функции. Если Т— период функции, то ее периодами будут также числа m•Т, где m=±1;±2,... Так, для у=sinx периодами будут числа ±2π;±4π; ±6π,... Основной период (наименьший положительный) — это период Т=2π. Вообще обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству ƒ(х+Т)=ƒ(х).

14.4. Обратная функция

Пусть задана функция у=ƒ(х) с областью определения D и множеством значений Е. Если каждому значению уєЕ соответствует единственное значение хєD, то определена функция х=φ(у) с областью определения Е и множеством значений D (см. рис. 102).

Такая функция φ(у)  называется  обратной к функции ƒ(х) и записывается в следующем виде: х=j(y)=f^-1(y).Про функции у=ƒ(х) и х=φ(у) говорят, что они являются взаимно обратными. Чтобы найти функцию х=φ(у), обратную к функции у=ƒ (х), достаточно решить уравнение ƒ(х)=у относительно х (если это возможно).

Примеры:

1. Для функции у=2х обратной функцией является функция х=у/2;

2.Для функции у=х2 хє[0;1] обратной функцией является х=√у; заметим, что для функции  у=х², заданной на отрезке [-1; 1], обратной не существует, т. к. одному значению у соответствует два значения х (так, если у=1/4, то х1=1/2, х2=-1/2).

Из определения обратной функции вытекает, что функция у=ƒ(х) имеет обратную тогда и только тогда, когда функция ƒ(х) задает взаимно однозначное соответствие между множествами D и Е. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).

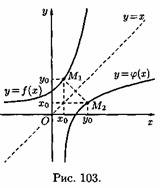
Заметим, что функция у=ƒ(х) и обратная ей х=φ(у) изображаются одной и той же кривой, т. е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через х, а зависимую переменную через у, то функция обратная функции у=ƒ(х) запишется в виде у=φ(х).

Это означает, что точка M₁(x_o;y_o) кривой у=ƒ(х) становится точкой М₂(у_о;х_о) кривой у=φ(х). Но точки M₁ и М₂симметричны относительно прямой у=х (см. рис. 103). Поэтому графики взаимно обратных функции у=ƒ(х) и у=φ(х) симметричны относительно биссектрисы первого и третьего координатных углов.