23. Производная сложной функции

Теорема 9 (производная сложной функции). Если а т. е. – сложная функция от ( ), причём и – дифференцируемые функции, то справедлива формула

(14)

Доказательство. Приращению аргумента функции отвечает приращение , а последнему приращению аргумента функции отвечает приращение . Таким образом, приращению аргумента в конечном счёте отвечает приращение рассматриваемой сложной функции зависящей от Поэтому производная этой сложной функции будет равна

(15)

Учтём, что так как функция является дифференцируемой, то, как было доказано ранее, она является непрерывной, поэтому, согласно второму определению непрерывности, для функции имеем Иначе говоря, если Теперь, умножив и поделив на запишем отношение в виде

В этом соотношении перейдём к пределу при (при этом ), кроме того, учтём, что предел правой части равен произведению пределов. В итоге получим

(16)

Так как функции и являются дифференцируемыми, то существуют конечные пределы

(17)

(18)

Согласно (16) из существования пределов (17) и (18) вытекает существование предела (15). Производные (15), (17) и (18) подставим в (16) вместо соответствующих пределов и придём к формуле (14). Теорема доказана.

Например, пусть дана сложная функция т. е. По формуле (14) имеем для производной этой сложной функции Здесь поэтому Аналогично получается формула для дифференцирования сложной функции, состоящей из трёх и большего числа составляющих функций. Запишем теперь формулу для дифференцирования сложной функции, состоящей из трех составляющих функций.

Пусть Имеем сложную функцию Её производная будет равна

Коротко правило дифференцирования сложной функции можно записать так: производная сложной функции равна произведению производных её составляющих по своим аргументам.

24.Производные степенной и показательной функций.

Теорема 10 (производная степенной функции). Если – любое действительное число, то или коротко:

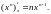
Доказательство. Пусть 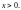От соотношения , возьмём натуральный логарифм: Далее продифференцируем эту функцию, при этом показатель степени как постоянный множитель вынесем за знак производной: Отсюда

(19)

Здесь производная левой части есть производная сложной функции. Так как логарифм зависит от который в свою очередь зависит от , то по формуле (14) имеем Но поэтому

(20)

Это выражение подставим в левую часть (19) и получим или Подставив сюда , получим то, что требуется. Теорема доказана. При 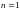теорема дает

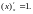
Доказательство теоремы проведено для случая Без обоснования отметим, что утверждение теоремы справедливо и для

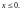
Замечание. При доказательстве теоремы соотношение сначала прологарифмировали, взяв натуральный логарифм от него, а затем полученное соотношение продифференцировали по Операция взятия логарифма и последующего дифференцирования называется логарифмическим дифференцированием, а выражение (20) называется логарифмической производной.

Теорема 11 (производная показательной функции). Если то Или коротко:

Доказательство теоремы аналогично предыдущему. При теорема дает

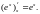
Наконец, отметим, что производные от степенно-показательных функций вида находятся с помощью логарифмического дифференцирования. Вычислим, например, производную функции . Для этого прологарифмируем, а затем продифференцируем обе части равенства . Получим или . Далее, . С учетом (20) имеем Отсюда