
- •1.Функция, способы задания
- •3.Сложная функция
- •4.Предел функции.
- •5.Единственность предела. Ограниченные функции.
- •6.Бесконечно малые функции, их свойства.
- •Следствия из теорем 2 – 5
- •7. Бесконечно большая функция, ее связь с бесконечно малой
- •8. Основные теоремы о пределах.
- •9. Первый замечательный предел
- •10.Второй замечательный предел.
- •11.Теорема о пределе возрастающей ограниченной функции. Число e . Натуральные логарифмы.
- •12. Сравнение бесконечно малых функций
- •13. Непрерывность функции в точке и на интервале
- •14. Приращение аргумента и функции. Второе определение непрерывности
- •15. Точки разрыва функции
- •16. Задача об определении скорости
- •17. Определение, механический и геометрический смыслы производной
- •18.Непрерывность дифференцируемой функции.
- •19. Производные алгебраической суммы, произведения, частного функций.
- •20. Производные sin X и cos X .
- •21. Производные tg X и ctg X
- •22. Производная логарифмической функции.
- •23. Производная сложной функции
- •24.Производные степенной и показательной функций.
- •25. Неявная функция и её производная
- •26. Обратная функция и её дифференцирование. Производные обратных
- •Обратная функция и ее производная
- •27. Дифференциал функции и его применение в приближенных вычислениях.
- •28. Производные и дифференциалы высших порядков
- •29.Теоремы Ферма и Ролля.
- •30. Теоремы Коши и Лагранжа
- •31. Правило Лопиталя
- •32. Возрастание и убывание функции. Монотонность. Интервалы монотонности. Достаточный признак монотонности функции.
- •33,34. Точки экстремума функции. Экстремумы функции. Необходимый признак экстремума. Критические точки. Наибольшее и наименьшее значения функции в замкнутом интервале.
- •35.Достаточный признак экстремума. Схема исследования функции на экстремум.
- •36. Выпуклость и вогнутость кривой. Точки её перегиба. Достаточные признаки выпуклости, вогнутости и точек перегиба кривой.
- •37.Асимптоты кривой.
- •38. Общая схема исследования функций и построения графиков
25. Неявная функция и её производная
Функция
![]() называется неявной,
если она определена соотношением, не
разрешенным относительно
:
называется неявной,
если она определена соотношением, не
разрешенным относительно
:
![]() (21)
(21)
где
![]() – известное выражение. Например, таковыми
являются соотношения
– известное выражение. Например, таковыми
являются соотношения
![]() , (22)
, (22)
![]() . (23)
. (23)
Если соотношение
(21) удаётся разрешить относительно
то мы придём к явному заданию. Например,
из (22) следует
![]() Но такой переход не всегда возможен,
например, в случае функции, заданной
уравнением (23). Однако всегда можно найти
производную неявной функции. Для этого
достаточно соотношение (21) продифференцировать
по
помня, что в нём
есть функция от
Сделаем это применительно к функции,
определённой неявно формулой (23).
Соотношение (23) продифференцируем по
учитывая, что слагаемое
Но такой переход не всегда возможен,
например, в случае функции, заданной
уравнением (23). Однако всегда можно найти
производную неявной функции. Для этого
достаточно соотношение (21) продифференцировать
по
помня, что в нём
есть функция от
Сделаем это применительно к функции,
определённой неявно формулой (23).
Соотношение (23) продифференцируем по
учитывая, что слагаемое
![]() – произведение двух функций, а слагаемое
– произведение двух функций, а слагаемое
![]() – сложная функция. Получим
– сложная функция. Получим
![]() Отсюда найдем искомую производную
Отсюда найдем искомую производную
![]() (24)
(24)
В этой формуле
– значение функции, соответствующее
взятому
,
согласно (23). В частности, из соотношения
(23) видно, что значению
![]() отвечает значение
отвечает значение
![]() т. к. при этих значениях соотношение
(23) выполняется. Поэтому при
производная
согласно (24), будет равна
т. к. при этих значениях соотношение
(23) выполняется. Поэтому при
производная
согласно (24), будет равна
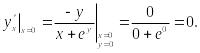
26. Обратная функция и её дифференцирование. Производные обратных
тригонометрических функций.
Обратная функция и ее производная
Пусть дана функция
.
Выразим из этого соотношения
через
и получим
![]() где
– аргумент, а
– функция. Эта последняя функция
называется обратной
к функции
где
– аргумент, а
– функция. Эта последняя функция
называется обратной
к функции
![]() Ясно, что на плоскости
этим функциям отвечает один график, так
как они представляют собой разные формы
записи одной и той же зависимости.
Ясно, что на плоскости
этим функциям отвечает один график, так
как они представляют собой разные формы
записи одной и той же зависимости.
Отметим следующий
геометрически очевидный факт: если
график функции
является восходящей (нисходящей) кривой,
т. е. с увеличением абсциссы
точки кривой её ордината
увеличивается (уменьшается), то обратная
к ней функция
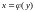 существует и будет однозначной, так как
каждому значению
из области значений функции
отвечает лишь одно значение
обратной функции
существует и будет однозначной, так как
каждому значению
из области значений функции
отвечает лишь одно значение
обратной функции
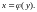
Теорема 12 (о
производной обратной функции).
Если
– функция, обратная по отношению к
функции
,
и
 то
то
![]() (25)
(25)
или коротко:
![]()
Доказательство.
Соотношение
определяет
функцию, обратную к
![]() поэтому
поэтому
![]() Полученное
соотношение продифференцируем по
помня, что в правой части стоит сложная
функция. Тогда будем иметь
Полученное
соотношение продифференцируем по
помня, что в правой части стоит сложная
функция. Тогда будем иметь
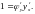 Отсюда
Отсюда
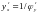 или
или
Производные обратных тригонометрических функций.
Функция
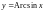 является обратной по отношению к функции
является обратной по отношению к функции
![]() График функции
График функции
![]() совпадает с графиком функции
.
Для любого
из интервала
совпадает с графиком функции
.
Для любого
из интервала
![]() на графике функции
(рис. 50) имеется бесчисленное множество
точек с абсциссой
их ординаты – значения функции.
Следовательно, эта функция является
бесконечнозначной. Возьмём ту часть
графика, где
на графике функции
(рис. 50) имеется бесчисленное множество
точек с абсциссой
их ординаты – значения функции.
Следовательно, эта функция является
бесконечнозначной. Возьмём ту часть
графика, где
![]() ;
на этом участке для каждого
;
на этом участке для каждого
![]() из интервала
из интервала
![]() имеется лишь одна точка с абсциссой
В дальнейшем под функцией
имеется лишь одна точка с абсциссой
В дальнейшем под функцией
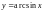 всегда будем понимать ветвь функции,
значения которой лежат в интервале
всегда будем понимать ветвь функции,
значения которой лежат в интервале
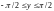 и
и
 .
.
Теорема 13.
Если
![]() то
то
![]() или коротко:
или коротко:
![]()
Д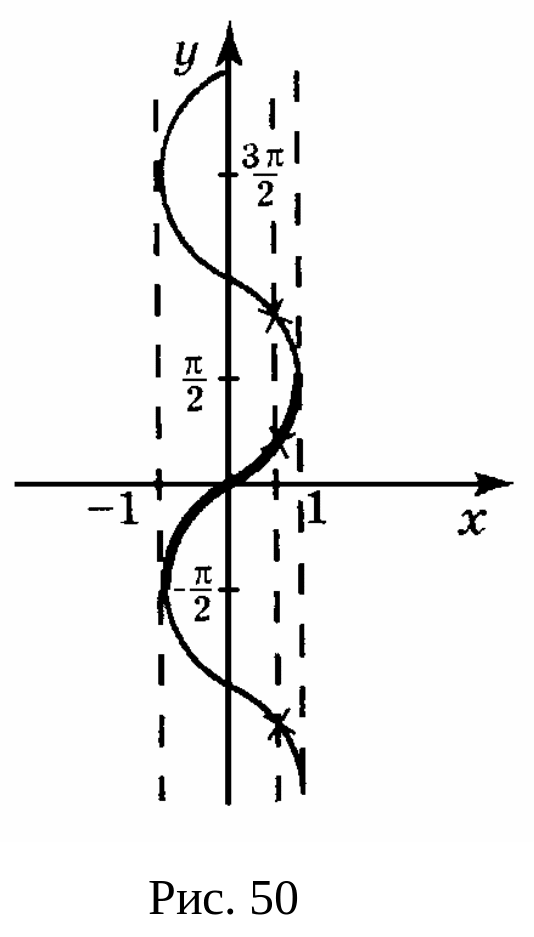 оказательство.
Производная функции
равна
оказательство.
Производная функции
равна
![]() Так как функция
Так как функция
![]() – обратная к
– обратная к
![]() то согласно (25) имеем
то согласно (25) имеем
![]()
 (26)
(26)
М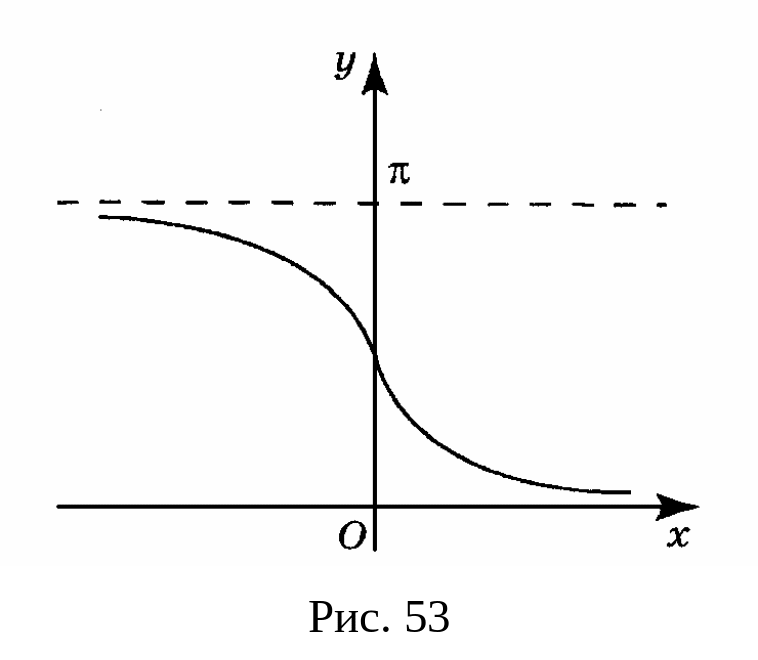 ы
нашли искомую производную, но пока она
выражена через
а не через
Но
следовательно,
ы
нашли искомую производную, но пока она
выражена через
а не через
Но
следовательно,
![]() нужно выразить через
нужно выразить через
![]() Как известно,
Как известно,
![]() но функция
принимает значения из интервала
но функция
принимает значения из интервала
![]() Для таких
как мы знаем,
Для таких
как мы знаем,
![]() следовательно, в предыдущей формуле мы
должны оставить знак «+». Таким образом,
следовательно, в предыдущей формуле мы
должны оставить знак «+». Таким образом,
![]() .
Так как
.
Так как
![]() то
то
![]() Подставив это выражение в (26), получим
утверждение теоремы 13.
Подставив это выражение в (26), получим
утверждение теоремы 13.
Ф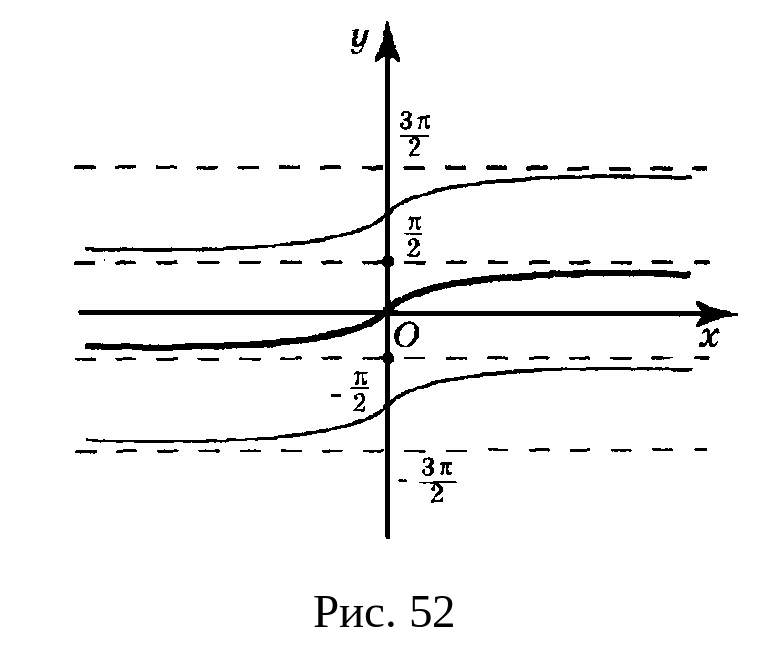 ункция
ункция
 – обратная по отношению к функции
– обратная по отношению к функции
![]() (см. рис. 51) В дальнейшем всегда под
функцией
(см. рис. 51) В дальнейшем всегда под
функцией
![]() будем понимать однозначную ветвь функции
,
значения которой лежат в интервале
будем понимать однозначную ветвь функции
,
значения которой лежат в интервале
![]() Для этой функции справедлива следующая
Для этой функции справедлива следующая
Теорема 14. Если
,
то
![]() или коротко:
или коротко:
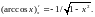
Доказательство проводится аналогично предыдущему.
Функция
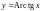 является обратной по отношению к функции
является обратной по отношению к функции
![]() (см. рис. 52). Выберем её однозначную
ветвь, для которой
(см. рис. 52). Выберем её однозначную
ветвь, для которой
![]() В дальнейшем всегда под функцией
В дальнейшем всегда под функцией
![]() будем понимать эту однозначную функцию.
Для нее справедлива
будем понимать эту однозначную функцию.
Для нее справедлива
Теорема 15.
Если
![]() то
то
![]() или коротко:
или коротко:
![]()
Доказательство проводится по аналогии с доказательством теоремы 13.
Функция
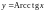 является обратной по отношению к функции
является обратной по отношению к функции
![]() .
Выберем её однозначную ветвь, а, именно,
в дальнейшем всегда под функцией
.
Выберем её однозначную ветвь, а, именно,
в дальнейшем всегда под функцией
![]() будем понимать однозначную функцию,
значения которой лежат в интервале
будем понимать однозначную функцию,
значения которой лежат в интервале
![]() (рис. 53). Для этой функции справедлива
(рис. 53). Для этой функции справедлива
Теорема 16. Если
![]() то
то
![]() или коротко:
или коротко:
![]()
Доказательство проводится по той же схеме, что и в случае теоремы 12.
