29.Теоремы Ферма и Ролля.

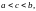Теорема Ролля. Если функция непрерывна в замкнутом интервале , дифференцируема во всех внутренних точках этого интервала и, кроме того, на концах интервала принимает одинаковые значения, то в этом интервале найдётся хотя бы одна точка в которой значение производной обращается в нуль.

Д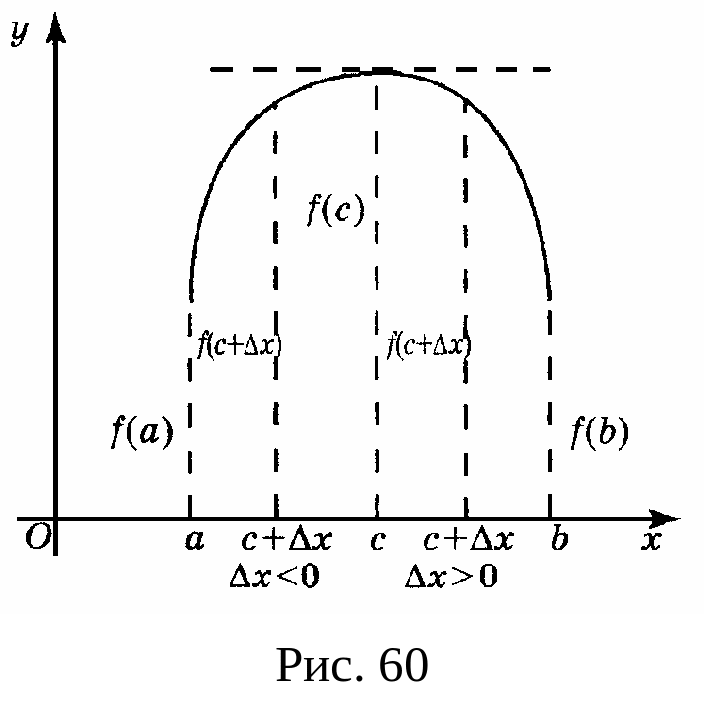 оказательство. Если функция не изменяется, т. е. остаётся постоянной (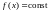 ), то 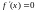и теорема для этого случая доказана. Пусть теперь функция с изменением изменяется. Пусть, например, начиная от точки с увеличением значение увеличивается, как показано на рис. 60. Тогда значение функции не является наибольшим ее значением на следова-тельно, по теореме 1 своё наибольшее значение функция примет в некоторой точке лежащей внутри интервала Следовательно, значение будет наибольшим значением функции в интервале т. е. для всех из

Теорема Ролля будет доказана, если мы покажем, что в точке в которой функция принимает наибольшее значение в интервале производная обращается в нуль. Таким образом, доказательство свелось к доказательству следующего утверждения.

Теорема Ферма. Если дифференцируемая в интервале функ-ция принимает в точке ( ) своё наибольшее значение в то в этой точке производная обращается в нуль, т. е.

Доказательство. Возьмём точку лежащую достаточно близко к точке считая, что – величина малая. Эта точка лежит правее при и левее при Так как есть наибольшее значение функции в интервале то ясно, что как для так и для , что можно переписать в виде для всех и Это неравенство умножим на число , положительное при и отрицательное при При этом знак неравенства не изменится при и изменится на обратный при . В результате получим

В этих неравенствах перейдём к пределу при и согласно теории пределов (теорема 15 главы 4) будем иметь

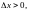
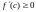По условию теоремы функция дифференцируема во всех внутренних точках интервала и в точке Это значит, что существует производная Но производная равна пределу, входящему в предыдущие неравенства. Этот предел является обычным двусторонним и существует независимо от знака . Следовательно, в двух предыдущих неравенствах пределы одинаковы и равны Поэтому предыдущие неравенства можно переписать так: при при 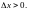Неравенства должны выполняться одновременно, а это возможно, если Теорема Ферма доказана, а вместе с ней доказана теорема Ролля.

Условие геометрически означает, что касательная к кривой в её точке с абсциссой параллельна оси В самом деле, вычисляемая в точке производная равна тангенсу угла наклона к оси абсцисс касательной к кривой в её точке с абсциссой Если эта производная равна нулю, то и т. е. касательная параллельна оси

30. Теоремы Коши и Лагранжа

Теорема Коши. Если функции и непрерывны в замкнутом интервале и дифференцируемы во всех внутренних точках этого интервала, причём всюду в этом интервале то в найдется хотя бы одна точка ( ), для которой справедлива формула

(3)

Доказательство. Возьмём функцию

(4)

Она удовлетворяет следующим условиям:

• непрерывна на действительно, непрерывна в этом интервале по условию, поэтому произведение дроби и также есть непрерывная функция на этом интервале согласно теореме о произведении непрерывных функций;

• разность, стоящая в правой части (4), – непрерывная функция согласно теореме о разности непрерывных функций;

• дифференцируема во всех внутренних точках интервала и имеет производную

(5)

где производные и существуют согласно условию теоремы;

• значения функции на концах равны, т. е. Чтобы непосредственно убедиться в этом, надо подставить в (4) сначала затем 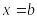и сравнить выражения.

Таким образом, функция удовлетворяет всем условиям теоремы Ролля, согласно которой на интервале найдется хотя бы одна точка в которой Это значит, что выражение (5) при обращается в нуль, т. е.

Учтя, что по условию теоремы, и поделив последнее соотношение на придём к формуле (3).

Теорема Лагранжа. Если функция непрерывна в замкнутом интервале и дифференцируема во всех внутренних точках этого интервала, то в найдется хотя бы одна точка ( ), для которой справедлива формула

(6)

Доказательство. Кроме функции указанной в теореме, возьмём ещё одну функцию Она дифференцируема всюду в интервале , так как имеет производную причём Кроме того, Таким образом, эта функция вместе с функцией удовлетворяют всем условиям теоремы Коши. Запишем формулу (3) для этих функций: Здесь Умножив это соотношение на , получим (6). Теорема доказана.