
- •1.Функция, способы задания
- •3.Сложная функция
- •4.Предел функции.
- •5.Единственность предела. Ограниченные функции.
- •6.Бесконечно малые функции, их свойства.
- •Следствия из теорем 2 – 5
- •7. Бесконечно большая функция, ее связь с бесконечно малой
- •8. Основные теоремы о пределах.
- •9. Первый замечательный предел
- •10.Второй замечательный предел.
- •11.Теорема о пределе возрастающей ограниченной функции. Число e . Натуральные логарифмы.
- •12. Сравнение бесконечно малых функций
- •13. Непрерывность функции в точке и на интервале
- •14. Приращение аргумента и функции. Второе определение непрерывности
- •15. Точки разрыва функции
- •16. Задача об определении скорости
- •17. Определение, механический и геометрический смыслы производной
- •18.Непрерывность дифференцируемой функции.
- •19. Производные алгебраической суммы, произведения, частного функций.
- •20. Производные sin X и cos X .
- •21. Производные tg X и ctg X
- •22. Производная логарифмической функции.
- •23. Производная сложной функции
- •24.Производные степенной и показательной функций.
- •25. Неявная функция и её производная
- •26. Обратная функция и её дифференцирование. Производные обратных
- •Обратная функция и ее производная
- •27. Дифференциал функции и его применение в приближенных вычислениях.
- •28. Производные и дифференциалы высших порядков
- •29.Теоремы Ферма и Ролля.
- •30. Теоремы Коши и Лагранжа
- •31. Правило Лопиталя
- •32. Возрастание и убывание функции. Монотонность. Интервалы монотонности. Достаточный признак монотонности функции.
- •33,34. Точки экстремума функции. Экстремумы функции. Необходимый признак экстремума. Критические точки. Наибольшее и наименьшее значения функции в замкнутом интервале.
- •35.Достаточный признак экстремума. Схема исследования функции на экстремум.
- •36. Выпуклость и вогнутость кривой. Точки её перегиба. Достаточные признаки выпуклости, вогнутости и точек перегиба кривой.
- •37.Асимптоты кривой.
- •38. Общая схема исследования функций и построения графиков
35.Достаточный признак экстремума. Схема исследования функции на экстремум.
Теорема 4 (первый достаточный признак экстремума функции). Критическая точка является точкой экстремума дифференцируемой всюду за исключением, быть может, точки функции если её производная изменяет знак при переходе через (с увеличением ). При перемене знака с «+» на «‑» – точка максимума функции, а при перемене с «‑» на «+» – точка минимума функции
Д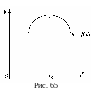 оказательство.
Пусть, например, производная
изменяет
знак с «+» на «‑» при переходе
через критическую точку
с увеличением
Это означает, что при
оказательство.
Пусть, например, производная
изменяет
знак с «+» на «‑» при переходе
через критическую точку
с увеличением
Это означает, что при
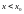 имеем
имеем
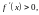 а при
а при
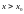 выполняется неравенство
выполняется неравенство
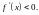 Но тогда согласно достаточному признаку
возрастания и убывания функции слева
от
имеется интервал возрастания функции,
а справа от
имеется интервал убывания функции.
Следовательно, график функции имеет
вид, представленный на рис. 65. Это
означает, что
– точка мак-симума функции
Вторая часть теоре-мы доказывается
аналогично.
Но тогда согласно достаточному признаку
возрастания и убывания функции слева
от
имеется интервал возрастания функции,
а справа от
имеется интервал убывания функции.
Следовательно, график функции имеет
вид, представленный на рис. 65. Это
означает, что
– точка мак-симума функции
Вторая часть теоре-мы доказывается
аналогично.
Рассмотрим схему исследования функции на экстремум. Чтобы найти экстремум функции , нужно:
найти критические точки этой функции, т. е. точки, в которых производная обращается в нуль или не существует;
каждую критическую точку исследовать с помощью достаточного признака экстремума;
найти экстремальные значения функции, подставив вместо в выражение точки экстремума.
Теорема 5
(второй достаточный признак экстремума
функции).
Пусть
– критическая точка дважды дифференцируемой
функции
т. е.
Тогда, если
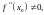 то
является точкой экстремума
а именно, точкой максимума при
то
является точкой экстремума
а именно, точкой максимума при
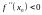 и точкой минимума при
и точкой минимума при
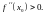
Доказательство.
Докажем
теорему для случая, когда
Нужно показать в этом случае, что
критическая точка
– точка минимума. При доказательстве
дополнительно предположим, что
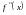 непрерывна в точке
Это означает, что
непрерывна в точке
Это означает, что

Возьмём число
равное
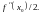 Это число положительное согласно
условию. Для этого числа согласно
определению предела функции
при
Это число положительное согласно
условию. Для этого числа согласно
определению предела функции
при
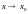 найдётся такое число
найдётся такое число
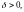 что для всех точек интервала
что для всех точек интервала
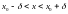 будет выполняться неравенство
будет выполняться неравенство
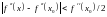 или равносильное ему неравенство
или равносильное ему неравенство
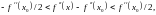 т. е.
т. е.
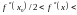
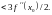 Итак, для всех
из интервала
выполняется неравенство
Итак, для всех
из интервала
выполняется неравенство
 Значит,
Значит,
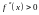 или
или
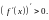 Отсюда ясно, что в указанном интервале
производная
возрастает, так как её производная
Отсюда ясно, что в указанном интервале
производная
возрастает, так как её производная
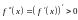 .
Поэтому большему значению аргумента
отвечают большие значения функции:
.
Поэтому большему значению аргумента
отвечают большие значения функции:
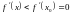 при
при
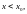
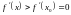 при
при
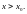 Итак, знак
изменяется с «‑» на «+» при переходе
через
с увеличением
Согласно первому достаточному признаку
экстремума приходим к выводу, что
– точка минимума. Вторая часть теоремы
доказывается аналогично.
Итак, знак
изменяется с «‑» на «+» при переходе
через
с увеличением
Согласно первому достаточному признаку
экстремума приходим к выводу, что
– точка минимума. Вторая часть теоремы
доказывается аналогично.
36. Выпуклость и вогнутость кривой. Точки её перегиба. Достаточные признаки выпуклости, вогнутости и точек перегиба кривой.
Кривая
называется выпуклой
в интервале
 если она лежит ниже любой своей касательной
в точках, абсциссы которых лежат в этом
интервале (см. рис. 68).
если она лежит ниже любой своей касательной
в точках, абсциссы которых лежат в этом
интервале (см. рис. 68).
К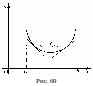
 ривая
называется вогнутой
в интервале
если она лежит выше любой своей касательной
в точках, абсциссы которых лежат в этом
интервале(см. рис. 69).
ривая
называется вогнутой
в интервале
если она лежит выше любой своей касательной
в точках, абсциссы которых лежат в этом
интервале(см. рис. 69).
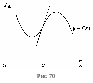
Точка кривой, отделяющая выпуклую часть от вогнутой, называется точкой перегиба. Ясно, что касательная к кривой в точке перегиба пересекает кривую, т. к. выпуклая часть лежит ниже касательной, а вогнутая – выше касательной (см. рис. 70).
Здесь и далее будем
считать, что функция
 дважды дифференцируема всюду в области
определения.
дважды дифференцируема всюду в области
определения.
Известно, что
вычисленная в точке
производная
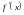 равна тангенсу угла
равна тангенсу угла
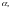 образованного с осью
образованного с осью
 касательной к кривой в её точке с
абсциссой
Для выпуклой кривой (см. рис. 68) с
увеличением
угол
касательной к кривой в её точке с
абсциссой
Для выпуклой кривой (см. рис. 68) с
увеличением
угол
 убывает, следовательно, убывает
убывает, следовательно, убывает
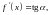 значит, производная
значит, производная
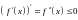 согласно необходимому признаку убывания
функции. Аналогично убедимся в том, что
если кривая
вогнутая, то
согласно необходимому признаку убывания
функции. Аналогично убедимся в том, что
если кривая
вогнутая, то
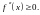 Итак, пришли к теореме.
Итак, пришли к теореме.
Теорема 6
(необходимые признаки выпуклости и
вогнутости кривой).
Если кривая
является выпуклой на
то в этом интервале
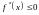 ;
если кривая
является вогнутой на
то в этом интервале
;
если кривая
является вогнутой на
то в этом интервале
Теорема 7
(достаточные признаки выпуклости и
вогнутости кривой).
Если
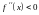 всюду в интервале
то в этом интервале кривая
выпуклая. Если
всюду в интервале
то в этом интервале кривая
выпуклая. Если
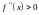 всюду в интервале
то в этом интервале кривая
вогнутая.
всюду в интервале
то в этом интервале кривая
вогнутая.
Доказательство.
Докажем первую часть теоремы. Пусть
всюду в интервале
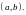 Тогда, согласно достаточному признаку
убывания функции, в этом интервале
убывает с увеличением
Значит,
Тогда, согласно достаточному признаку
убывания функции, в этом интервале
убывает с увеличением
Значит,
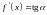 убывает всюду в интервале
Следовательно, кривая
является выпуклой, что очевидно
геометрически. Теорема доказана.
убывает всюду в интервале
Следовательно, кривая
является выпуклой, что очевидно
геометрически. Теорема доказана.
Теорема 8
(необходимый
признак точки перегиба).
Если
– абсцисса точки перегиба кривой
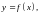 то
то
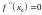 или не существует.
или не существует.
Доказательство.
Точка перегиба
отделяет выпуклую часть от вогнутой,
следовательно, она одновременно
принадлежит обеим указанным частям
кривой. Будем считать, что вторая
производная
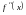 существует и непрерывна в точке
.
Для выпуклой
части кривой
согласно необходимому признаку выпуклости
кривой,
существует и непрерывна в точке
.
Для выпуклой
части кривой
согласно необходимому признаку выпуклости
кривой,
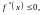 поэтому
поэтому
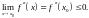 Для вогнутой части кривой
согласно необходимому признаку вогнутости
кривой,
Для вогнутой части кривой
согласно необходимому признаку вогнутости
кривой,
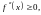 поэтому
поэтому
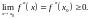 Но эти два соотношения должны выполняться
одновременно, следовательно,
Но эти два соотношения должны выполняться
одновременно, следовательно,
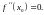 Теорема доказана.
Теорема доказана.
Абсциссой точки
перегиба может служить и значение
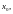 при котором
при котором
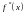 не существует. Покажем это на примере
кривой
не существует. Покажем это на примере
кривой
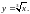 Здесь
Здесь

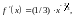
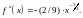 Отметим, что при
вторая производная
не существует, т. е. не существует
Отметим, что при
вторая производная
не существует, т. е. не существует
 .
Кроме того, видим, что
.
Кроме того, видим, что
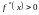 при
при
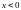 ,
а при
,
а при
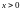 имеем
имеем
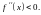 Значит, по теореме 7 при
кривая вогнутая, при
- выпуклая. Это означает, что
есть абсцисса точки перегиба рассматриваемой
кривой. Это также очевидно из графика
функции (см. рис. 71).
Значит, по теореме 7 при
кривая вогнутая, при
- выпуклая. Это означает, что
есть абсцисса точки перегиба рассматриваемой
кривой. Это также очевидно из графика
функции (см. рис. 71).
Теорема 9
(достаточный
признак точки перегиба).
Точка кривой
кривой
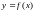 является точкой перегиба, если
является точкой перегиба, если
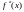 обращается в нуль или не существует при
обращается в нуль или не существует при
 и знак
второй производной
и знак
второй производной
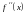 изменяется при переходе
через
(с увеличением
).
При перемене знака с «‑» на «+»
участок выпуклости сменяется участком
вогнутости, а при перемене с «+» на «‑»
участок вогнутости сменяется участком
выпуклости.
изменяется при переходе
через
(с увеличением
).
При перемене знака с «‑» на «+»
участок выпуклости сменяется участком
вогнутости, а при перемене с «+» на «‑»
участок вогнутости сменяется участком
выпуклости.
Доказательство.
Пусть знак
изменяется с «‑» на «+» при переходе
через
с увеличением
т. е. при
имеем
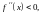 а при
получим
а при
получим
 Тогда, согласно достаточному признаку
выпуклости и вогнутости кривой, слева
от
лежит участок выпуклости кривой, а
справа от
– участок вогнутости. Следовательно,
– абсцисса точки перегиба кривой
Тогда, согласно достаточному признаку
выпуклости и вогнутости кривой, слева
от
лежит участок выпуклости кривой, а
справа от
– участок вогнутости. Следовательно,
– абсцисса точки перегиба кривой
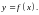 Вторая часть теоремы доказывается
аналогично.
Вторая часть теоремы доказывается
аналогично.
Для нахождения точек перегиба кривой требуется:
1)найти точки, в которых обращается в нуль или не существует;
2)каждую такую точку исследовать с помощью достаточного признака точки перегиба;
3)найти ординаты точек перегиба, подставив их абсциссы в выражение вместо
