9. Первый замечательный предел

Д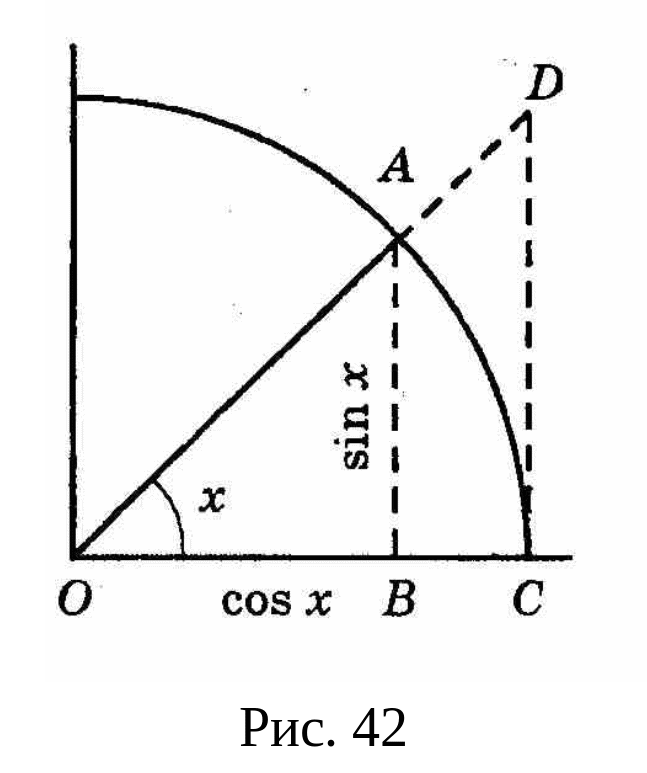 окажем равенство . Возьмем круг единичного радиуса. Пусть есть угол между векторами и , измеренный в радианах (см. рис. 42). Будем считать угол положительным, если он отсчитывается против хода часовой стрелки от вектора , и отрицательным, если отсчёт ведётся в противоположном направлении. Будем считать пока . Из рис. 42 видно, что , , , а также что и при . Это верно и при . Площади треугольников и кругового сектора, указанных на рис. 42, связаны соотношением которое принимает вид или (после умножения на положительное число ) . В последнем неравенстве перейдём к обратным величинам, при этом знаки неравенства изменятся на обратные:

. (13)

Последнее неравенство получено для . Пусть теперь . Тогда и справедлива формула (13), т. е. . Учитывая, что и , опять придём к неравенству (13), но уже для .

Итак, неравенство (13) справедливо как для , так и для . Перейдем в нем при к пределу (к обычному пределу, когда , принимая как положительные, так и отрицательные значения). Однако крайние части (13) имеют один и тот же предел, равный 1. Поэтому по теореме 13 получим предел , который называют «первым замечательным пределом».

Пример.

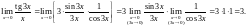
10.Второй замечательный предел.

Теорема 17. Функция при имеет предел, равный :

. (14)

Предел (14) называют «вторым замечательным пределом».

Пример.

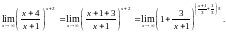
Пусть 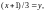при этом 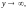когда 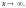Тогда последний предел примет вид

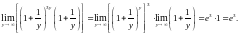
Логарифм называется натуральным, если его основание равно , т. е. . Этот логарифм обозначают .

Пусть . Тогда по определению логарифма . От последнего соотношения возьмём десятичный логарифм и получим . По свойству логарифма будем иметь . Но , следовательно,

. (15)

В этой формуле – известное число (т. к. – число известное, то и его десятичный логарифм известен: ), поэтому формула (15) выражает десятичный логарифм через его натуральный логарифм. Ясно, что и, наоборот, по можно найти .

11.Теорема о пределе возрастающей ограниченной функции. Число e . Натуральные логарифмы.

Теорема 15. Всякая возрастающая ограниченная последовательность (функция натурального аргумента) имеет конечный предел.

Эта теорема утверждает только лишь существование предела, но не указывает, как его найти.

Теорема 16. Функция натурального аргумента имеет при предел, заключённый между числами 2 и 3.

При доказательстве этой теоремы сначала устанавливают, что эта функция является возрастающей и ограниченной. Поэтому согласно теореме 15 предел функции существует. Его обозначают через и пишут

.

Можно показать (принимается без доказательства), что число является иррациональным. Его приближённое значение

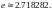
Логарифм называется натуральным, если его основание равно , т. е. . Этот логарифм обозначают .

Пусть . Тогда по определению логарифма . От последнего соотношения возьмём десятичный логарифм и получим . По свойству логарифма будем иметь . Но , следовательно,

. (15)

В этой формуле – известное число (т. к. – число известное, то и его десятичный логарифм известен: ), поэтому формула (15) выражает десятичный логарифм через его натуральный логарифм. Ясно, что и, наоборот, по можно найти .