19. Производные алгебраической суммы, произведения, частного функций.

Теорема 3. Если и – дифференцируемые функции, то:

(a)

(b)

(c)

Доказательство. Докажем лишь последнее утверждение (c) ((a) и (b) доказываются аналогично).

По формуле (8), в которой вместо нужно взять , имеем

(9)

Разности суть соответственно приращения функций и Отсюда находим Эти суммы подставим в (9) и получим

(10)

Выражение в числителе правой части этой формулы приведем к общему знаменателю и представим ее в виде

(11)

Предел правой части формулы (11) равен пределу числителя, делённому на предел знаменателя. Но предел числителя равен разности пределов, так как там стоит предел разности. Предел знаменателя равен сумме пределов слагаемых, но здесь пределы берутся при когда следовательно, и не изменяются, т. е. являются постоянными, и эти множители выносятся за знак предела. Поэтому (11) примет вид

(12)

Так как – дифференцируемые функции, то существуют пределы и Кроме того, по условию теоремы – дифференцируемая функция, значит, она непрерывна, поэтому согласно второму определению непрерывной функции Подставив последние три предела в (12), получим формулу (с).Теорема доказана.

Следствие из утверждения ( ) теоремы 3. Если – постоянная,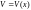 – дифференцируемая функция, то

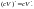
В самом деле, когда , имеем , и формула ( ) теоремы 2 даёт

20. Производные sin X и cos X .

Теоремы 4 и 5 (производные синуса и косинуса). Если то Если то Или коротко и

Доказательство. Докажем первую теорему (вторая доказывается аналогично).

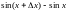
Дифференцируемая функция согласно формуле (8) имеет производную Числитель формулы справа можно разложить по известной из тригонометрии формуле разности синусов: Подставив это выражение в предыдущую формулу, получим Справа предел произведения равен произведению пределов, поэтому

(13)

Но первый предел равен единице, т. к. представляет собой «первый замечательный предел», в котором А второй предел, в силу непрерывности косинуса, при 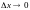и равен Подставив эти пределы в формулу (13), получим то, что требуется. Теорема доказана.

21. Производные tg X и ctg X

Теоремы 6 и 7 (производные тангенса и котангенса). Если то Если то Или коротко: и

Доказательство. Докажем первую теорему (вторая доказывается аналогично). С учётом формулы ( ) теоремы 2 имеем

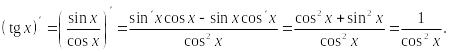
22. Производная логарифмической функции.

Теорема 8 (производная логарифмической функции). Если то Или коротко:

Доказательство. Согласно определению производной

В числителе воспользуемся тем, что разность логарифмов равна логарифму отношения, поэтому

Выражение под знаком предела разделим и умножим на затем множитель вынесем за знак предела, так как он не зависит от Получим

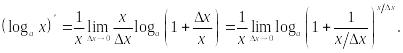
Так как логарифм – непрерывная функция, знаки предела и логарифма можно поменять местами, поэтому

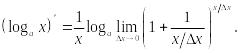
При фиксированном и имеем . Значит, согласно теореме 17 главы 4 Поэтому . Пришли к утверждению теоремы.

В частности, при имеем и Тогда утверждение теоремы примет вид