
- •1.Функция, способы задания
- •3.Сложная функция
- •4.Предел функции.
- •5.Единственность предела. Ограниченные функции.
- •6.Бесконечно малые функции, их свойства.
- •Следствия из теорем 2 – 5
- •7. Бесконечно большая функция, ее связь с бесконечно малой
- •8. Основные теоремы о пределах.
- •9. Первый замечательный предел
- •10.Второй замечательный предел.
- •11.Теорема о пределе возрастающей ограниченной функции. Число e . Натуральные логарифмы.
- •12. Сравнение бесконечно малых функций
- •13. Непрерывность функции в точке и на интервале
- •14. Приращение аргумента и функции. Второе определение непрерывности
- •15. Точки разрыва функции
- •16. Задача об определении скорости
- •17. Определение, механический и геометрический смыслы производной
- •18.Непрерывность дифференцируемой функции.
- •19. Производные алгебраической суммы, произведения, частного функций.
- •20. Производные sin X и cos X .
- •21. Производные tg X и ctg X
- •22. Производная логарифмической функции.
- •23. Производная сложной функции
- •24.Производные степенной и показательной функций.
- •25. Неявная функция и её производная
- •26. Обратная функция и её дифференцирование. Производные обратных
- •Обратная функция и ее производная
- •27. Дифференциал функции и его применение в приближенных вычислениях.
- •28. Производные и дифференциалы высших порядков
- •29.Теоремы Ферма и Ролля.
- •30. Теоремы Коши и Лагранжа
- •31. Правило Лопиталя
- •32. Возрастание и убывание функции. Монотонность. Интервалы монотонности. Достаточный признак монотонности функции.
- •33,34. Точки экстремума функции. Экстремумы функции. Необходимый признак экстремума. Критические точки. Наибольшее и наименьшее значения функции в замкнутом интервале.
- •35.Достаточный признак экстремума. Схема исследования функции на экстремум.
- •36. Выпуклость и вогнутость кривой. Точки её перегиба. Достаточные признаки выпуклости, вогнутости и точек перегиба кривой.
- •37.Асимптоты кривой.
- •38. Общая схема исследования функций и построения графиков
1.Функция, способы задания
Пусть
![]() – переменная величина,
– переменная величина,
![]() – множество ее значений,
– множество ее значений,
![]() – другая переменная величина и
– другая переменная величина и
![]() – множество её значений.
– множество её значений.
Функцией
называется правило, по которому каждому
значению
из множества
ставится в соответствие определённое
значение
из множества
при условии, что каждое значение
из множества
отвечает хотя бы одному
из
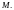 Переменная
называется независимой
переменной
или аргументом,
а зависимая переменная
– функцией.
Множество
называется областью
определения функции,
а
– областью
значений
функции. Введённая функция обозначается
Переменная
называется независимой
переменной
или аргументом,
а зависимая переменная
– функцией.
Множество
называется областью
определения функции,
а
– областью
значений
функции. Введённая функция обозначается
![]() (здесь
(здесь
![]() означает не переменную, а вышеуказанное
правило, устанавливающее соответствие
между
и
).
Говорят, что функция
отображает множество
на множество
означает не переменную, а вышеуказанное
правило, устанавливающее соответствие
между
и
).
Говорят, что функция
отображает множество
на множество
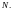 Вместо
применяются и другие буквы, например,
Вместо
применяются и другие буквы, например,
![]() ,
,

![]() и т. д.
и т. д.
Графический способ задания функции – это способ задания функции с помощью её графика.
Графиком функции
называется множество точек на плоскости
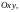 для каждой из которых абсцисса
равна значению аргумента, а ордината
равна соответствующему значению функции
.
для каждой из которых абсцисса
равна значению аргумента, а ордината
равна соответствующему значению функции
.
Как правило, будем рассматривать функции, графики которых представляют собой сплошные линии или линии, состоящие из нескольких сплошных кривых. Ясно, что соотношение является уравнением этой линии.
Аналитический
способ задания функции. Здесь
функция задаётся формулой, например,
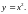 Однако функция может задаваться
одновременно несколькими формулами
для различных интервалов изменения
Однако функция может задаваться
одновременно несколькими формулами
для различных интервалов изменения
 Например,
Например,
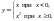
Но если функция
задана одной формулой, без дополнительного
указания области определения, то под
последней понимается совокупность всех
значений
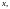 для которых эта формула имеет смысл и
по которым можно вычислить соответствующие
значения функции.
для которых эта формула имеет смысл и
по которым можно вычислить соответствующие
значения функции.
2.
Элементарной
называется функция, определяемая одной
формулой, составленной из основных
элементарных функций, с помощью конечного
числа четырёх арифметических действий
![]() и с помощью конечного числа операций
взятия функции от функции.
и с помощью конечного числа операций
взятия функции от функции.
Основные элементарные функции:
постоянная функция
![]() ;
;
степенная функция
![]() ,
,
![]() – любое действительное число;
– любое действительное число;
показательная
функция
![]()
![]() ;
;
логарифмическая
функция
![]() ;
;
тригонометрические
функции
![]()
![]()
![]()
![]() ;
;
обратные
тригонометрические функции
![]()
![]()
![]() ,
,
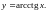
3.Сложная функция
Определение
сложной функции. Дана
функция
![]() ,
причём аргумент
,
причём аргумент
![]() является функцией от
,
т. е.
является функцией от
,
т. е.
![]() .
Область значений функции
является частью области определения
функции
.
Следовательно, каждому
из области определения
.
Область значений функции
является частью области определения
функции
.
Следовательно, каждому
из области определения
![]() отвечает определённое значение
,
а этому значению
отвечает определённое значение
.
Таким образом, каждому указанному
отвечает определённое значение
.
Это означает, что
есть функция от
.
Она называется сложной
функцией от
и записывается в виде
отвечает определённое значение
,
а этому значению
отвечает определённое значение
.
Таким образом, каждому указанному
отвечает определённое значение
.
Это означает, что
есть функция от
.
Она называется сложной
функцией от
и записывается в виде![]() ,
где
,
где
![]() – внутренняя функция,
– внешняя функция,
– промежуточный аргумент. Например,
пусть
– внутренняя функция,
– внешняя функция,
– промежуточный аргумент. Например,
пусть
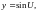 где
где
![]() ,
тогда получим сложную функцию
,
тогда получим сложную функцию
![]() .
.
4.Предел функции.
1.Пусть
– переменная величина, которая принимает
положительные значения и неограниченно
увеличивается. В этом случае будем
говорить, что
стремится к
плюс бесконечности
и писать
![]() .
Пусть при этом заданная функция
принимает значения, всё более и более
близкие к некоторому числу
.
Пусть при этом заданная функция
принимает значения, всё более и более
близкие к некоторому числу
![]() ,
в том смысле, что величина
,
в том смысле, что величина
![]() уменьшается и приближается к нулю. В
этом случае будем говорить, что число
есть предел
функции
при
.
уменьшается и приближается к нулю. В
этом случае будем говорить, что число
есть предел
функции
при
.
Определение.
Число
называется пределом
функции
при
,
если для любого положительного числа
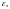 каким бы малым оно ни было, найдётся
такое положительное число
каким бы малым оно ни было, найдётся
такое положительное число
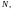 что для всех
что для всех
![]() выполняется неравенство
выполняется неравенство
 т. е. символически
т. е. символически
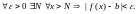 В этом случае будем
писать
В этом случае будем
писать

2. Пусть переменная
принимает отрицательные значения, и
абсолютная величина
![]() возрастает. В этом случае говорят, что
возрастает. В этом случае говорят, что
![]() .
Дадим определение предела функции
при
символически. Число
называется пределом
функции
при
,
если
.
Дадим определение предела функции
при
символически. Число
называется пределом
функции
при
,
если
 В этом случае пишут
В этом случае пишут
![]() .
.
3. Пусть
изменяется, принимая как положительные,
так и отрицательные значения, абсолютная
величина
неограниченно увеличивается. Тогда
говорят, что
стремится к
бесконечности,
и пишут
![]() .
Число
называется пределом
функции
при
,
если для любого положительного
.
Число
называется пределом
функции
при
,
если для любого положительного
![]() найдётся такое число
найдётся такое число
![]() ,
что для всех
,
абсолютная величина которых
,
что для всех
,
абсолютная величина которых
![]() ,
имеет место неравенство
т. е.
,
имеет место неравенство
т. е.
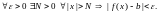
В этом случае пишут
![]() .
.
4. Пусть
![]() – заданное число. Рассмотрим предел
функции
,
когда
– заданное число. Рассмотрим предел
функции
,
когда
![]() и
и
![]() .
Число
называется пределом
слева функции
при
,
если для любого числа
.
Число
называется пределом
слева функции
при
,
если для любого числа
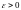 найдётся такое число
найдётся такое число
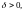 что для всех точек интервала
что для всех точек интервала
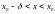 выполняется неравенство
выполняется неравенство
![]() ,
каким бы малым
,
каким бы малым
 ни было. Сказанное можно записать
символически в виде
ни было. Сказанное можно записать
символически в виде
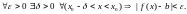
В этом случае пишут
![]() .
.
По аналогии дадим определение предела функции справа при . Число называется пределом функции при справа, если

В этом случае пишут
![]() .
.
5. Число
называется (двусторонним)
пределом функции
при
,
если для любого числа
![]() ,
каким бы малым оно ни было, найдётся
такое число
что для всех точек интервала
,
каким бы малым оно ни было, найдётся
такое число
что для всех точек интервала
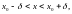 отличных от
,
выполняется неравенство
,
т. е.
отличных от
,
выполняется неравенство
,
т. е.
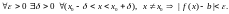
В этом случае пишут
![]() .
.
