Кинематика Лекция 4. Кинематика точки

 

 

4.1. Некоторые определения

 

            Кинематика – это раздел теоретической механики, в котором изучают движение тел без учета их масс и действующих на них сил. Движение всегда рассматривают по отношению к некоторой определенной системе отсчета.

            В кинематике имеют место две основные задачи:

            1) установление закона движения, т.е. математического способа задания положения точки или тела относительно выбранной системы отсчета в любой момент времени;

            2) определение по заданному закону движения кинематических характеристик этого движения, к которым относятся траектория, скорость и ускорение точки, угловая скорость и угловое ускорение тела.

            Наиболее простым объектом, изучаемым в кинематике, является точка. Траекторией точки называют геометрическое место положений движущейся точки в рассматриваемой системе отсчета. Если траектория точки является прямой линией, то движение называют прямолинейным, в противном случае – криволинейным.

 

4.2. Способы задания движения точки

 

            4.2.1. Векторный способ. Выберем некоторую точку O, неподвижную в рассматриваемой системе отсчета (рис. 4.1). Тогда положение движущейся точки M в любой момент можно определить ее радиус-векто-ром  . Зависимость радиус-вектора   от времени

                     (4.1)

называют уравнением движения точки в векторной форме.

 

            

 

 

 

 

 

 

 

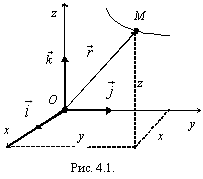
4.2.2. Координатный способ. Положение точки относительно некоторой координатной системы определяют ее координатами. Рассмотрим прямоугольную декартову систему координат Oxyz (см. рис. 4.1) и зададим координаты x, y, z как функции времени:

.                                  (4.2)

            Уравнения (4.2) называют уравнениями движения точки в координатной форме. В этом случае радиус-вектор точки M

,                               (4.3)

где   – орты координатных осей.

            4.2.3. Естественный способ. Пусть известна траектория точки (рис. 4.2). Выберем на ней начало отсчета O криволинейной координаты S и положительное направление отсчета, тогда положение точки M в любой момент времени можно определить, воспользовавшись зависимостью

S = S(t),                                                     (4.4)

к оторую называют уравнением движения точки в естественной форме.

            Введем подвижную систему координат, начало которой совпадает с движущейся точкой М, и будем использовать ее в дальнейшем. Оси этой системы координат, называют естественным трехгранником или скоростными осями. Они направлены так: ось M – по касательной к траектории в сторону увеличения координаты S, ось Mn – по главной нормали к траектории в сторону ее вогнутости, а ось Mb дополняет систему до правой;   – орты координатных осей.

 

4.3. Определение скорости точки

 

            Скорость точки характеризует изменение ее положения в рассматриваемой системе отсчета с течением времени.

            4.3.1. Векторный способ. Пусть за время t точка переместилась из положения M в положение   и ее радиус-вектор изменился на величину   (рис. 4.3). Тогда средней скоростью точки за интервал времени t будет отношение

.

э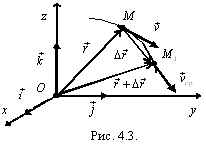 тот вектор направлен по хорде   и зависит от величины интервала времени t.

            Предел средней скорости

     (4.5)

называют скоростью точки в данный момент времени или просто скоростью точки. В уравнении (4.5) переменная с точкой над ней обозначает производную по времени.

            Итак, скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора точки в рассматриваемой системе отсчета. При стремлении t к нулю точка   приближается к точке M, и хорда   в пределе занимает положение касательной к траектории. Таким образом, вектор скорости   направлен по касательной к траектории в сторону движения точки.

            Единица измерения скорости в системе СИ – 1 м/с.

            4.3.2. Координатный способ. Пусть движение точки задано координатным способом (4.2), тогда ее радиус-вектор  . Учитывая, что орты   постоянны, из уравнения (4.5) получим

.

Таким образом, запишем проекции вектора скорости на координатные оси:

.                        (4.6)

По этим проекциям можно определить модуль вектора скорости

                                             (4.7)

и его направляющие косинусы, т.е. косинусы углов между вектором скорости и положительными направлениями координатных осей:

.                  (4.8)

            4.3.3. Естественный способ. Пусть точка движется по известной траектории, и ее положение определяется криволинейной координатой S (рис. 4.4). Предположим, что за время t радиус-вектор точки получил приращение  , а координата S – приращение S. Определим скорость точки

.             (4.9)

             Рассмотрим вектор  . Его модуль равен пределу отношения длины хорды   к длине стягиваемой ею дуги:

.

Направление вектора   совпадает с направлением  при движении точки в сторону увеличения координаты S (S  0) и противоположно   при движении в противоположную сторону (S  0). Таким образом, вектор   всегда направлен по касательной к траектории в сторону увеличения координаты S, т.е. он является единичным вектором касательной к траектории точки

.                                                   (4.10)

На основании этого из уравнения (4.9) получим

.                                               (4.11)

            Скалярную величину   называют алгебраической скоростью точки. Она представляет собой проекцию вектора скорости на касательную к траектории. Знак алгебраической скорости определяет направление движения точки: при    0 она движется в сторону увеличения координаты S, при   0 – в противоположную сторону. Модуль вектора скорости  .