
- •Статика Лекция 1. Основные понятия и аксиомы статики. Система сходящихся сил
- •1.1. Основные понятия статики
- •1.2. Аксиомы статики
- •1.3. Связи и их реакции
- •1.4. Система сходящихся сил
- •1.5. Условия равновесия системы сходящихся сил
- •1.6. Решение задач статики
- •Лекция 2. Теория пар
- •2.1. Момент силы относительно точки и оси
- •2.2. Пара сил и ее момент
- •2.3. Теоремы о парах
- •2.4. Условия равновесия системы пар сил
- •Вопросы для самоконтроля
- •Лекция 3. Основная теорема статики и условия равновесия пространственной системы сил
- •3.1. Лемма о параллельном переносе силы
- •3.2. Основная теорема статики
- •3.3. Приведение системы сил к двум силам
- •3.4. Условия равновесия пространственной системы сил
- •3.5. Теорема Вариньона
- •3.6. Условия равновесия плоской системы сил
- •Кинематика Лекция 4. Кинематика точки
- •4.1. Некоторые определения
- •4.2. Способы задания движения точки
- •4.3. Определение скорости точки
- •4.4. Определение ускорения точки
- •4.5. Частные случаи движения точки
- •Лекция 5. Простейшие движения твердого тела
- •5.1. Поступательное движение твердого тела
- •5.2. Вращение твердого тела вокруг неподвижной оси
- •5.3. Угловая скорость твердого тела
- •5.4. Угловое ускорение твердого тела
- •5.5. Частные случаи вращательного движения
- •5.6. Скорость и ускорение точки тела, вращающегося вокруг
- •Лекция 6. Сложное движение точки
- •6.1. Основные определения
- •6.2. Определение абсолютной скорости точки
- •6.3. Определение абсолютного ускорения точки
- •Лекция 7. Плоское движение твердого тела
5.5. Частные случаи вращательного движения
Вращательное
движение называют равномерным, если
угловая скорость тела не изменяется,
т.е. ![]() = const.
Интегрируя это соотношение, получим
уравнение равномерного вращения
= const.
Интегрируя это соотношение, получим
уравнение равномерного вращения
![]() ,
(5.7)
,
(5.7)
где ![]() –
начальный угол поворота тела.
–
начальный угол поворота тела.
Вращательное
движение называют равнопеременным, если
угловое ускорение тела не изменяется,
т.е. ![]() = const,
откуда после интегрирования получим
= const,
откуда после интегрирования получим
![]() .
(5.8)
.
(5.8)
Так
как из выражения (5.8) следует, что ![]() ,
можно записать уравнение равнопеременного
вращения
,
можно записать уравнение равнопеременного
вращения
![]() .
(5.9)
.
(5.9)
Из двух последних равенств нетрудно получить следующее соотношение
![]() .
(5.10)
.
(5.10)
5.6. Скорость и ускорение точки тела, вращающегося вокруг
неподвижной оси
Рассмотрим точку М, находящуюся на расстоянии h от оси вращения. Эта точка движется по окружности радиусом h. Зададим движение точки M естественным способом. Начало отсчета криволинейной координаты S выберем в точке O, где окружность пересекается с неподвижной полуплоскостью (рис. 5.4). Тогда OCM = и уравнение движения точки M примет вид:
![]() .
(5.11)
.
(5.11)
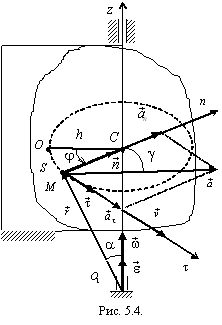
Введем
естественную координатную систему Mn,
орты осей ![]() и
воспользуемся полученными в 4-й лекции
соотношениями.
и
воспользуемся полученными в 4-й лекции
соотношениями.
Скорость точки М:
![]() ,
(5.12)
,
(5.12)
ее модуль:
![]() .
(5.13)
.
(5.13)
Ускорение точки М имеет касательную и нормальную составляющие:
![]() .
(5.14)
.
(5.14)
Касательное ускорение
![]() ,
(5.15)
,
(5.15)
его модуль
![]() .
(5.16)
.
(5.16)
Нормальное ускорение
![]() ,
(5.17)
,
(5.17)
его модуль
![]() .
(5.18)
.
(5.18)
Модуль ускорения точки М
![]() .
(5.19)
.
(5.19)
Угол между
вектором ускорения ![]() и
осью n определим из соотношения:
и
осью n определим из соотношения:
![]() .
(5.20)
.
(5.20)
Так как угловая скорость и угловое ускорение характеризуют движение тела в целом, из формул (5.12)-(5.20) следует, что скорости и ускорения точек тела, вращающегося вокруг неподвижной оси, пропорциональны расстояниям от этих точек до оси вращения, а углы в каждый момент времени одинаковы для всех точек.
Введем
в рассмотрение векторы угловой скорости
,
углового ускорения ![]() и
радиус-вектор
точки M (см.
рис. 5.4). Тогда вектор скорости может
быть представлен векторным произведением
и
радиус-вектор
точки M (см.
рис. 5.4). Тогда вектор скорости может
быть представлен векторным произведением
![]() .
(5.21)
.
(5.21)
Это соотношение имеет название формулы Эйлера.
Легко
убедиться в справедливости формулы
(5.21). Действительно, правило векторного
произведения показывает, что направление
вектора ![]() совпадает
с направлением вектора
(см.
рис. 5.4). Его модуль:
совпадает
с направлением вектора
(см.
рис. 5.4). Его модуль:
![]() .
.
Продифференцируем формулу Эйлера по времени:
![]()
или
![]() .
(5.22)
.
(5.22)
Покажем, что две составляющие ускорения точки в формуле (5.22) являются касательным и нормальным ускорениями:
![]() ;
(5.23)
;
(5.23)
![]() .
(5.24)
.
(5.24)
Совпадение направлений векторов в левой и правой частях равенств (5.23), (5.24) проверяют по правилу векторного произведения. Их модули:
![]() ;
;
![]() .
.
Пример. Груз
1 подвешен на нити, намотанной на барабан
лебедки радиусом ![]() =
0,1 м (рис. 5.5). С барабаном жестко соединена
шестерня 2 радиусом
=
0,1 м (рис. 5.5). С барабаном жестко соединена
шестерня 2 радиусом ![]() =
0,15 м, которая находится в зацеплении с
шестерней 3 радиусом
=
0,15 м, которая находится в зацеплении с
шестерней 3 радиусом ![]() =
0,12 м.
=
0,12 м.
Определить
скорость и ускорение точки М шестерни
3, находящейся на расстоянии ![]() =
0,08 м от оси вращения в момент времени t =
0,2 с, если груз 1 движется по закону
=
0,08 м от оси вращения в момент времени t =
0,2 с, если груз 1 движется по закону ![]() (м).
(м).
Найдем
модуль скорости груза 1: ![]() .
Такую же скорость имеют все точки обода
барабана, поэтому модуль его угловой
скорости
.
Такую же скорость имеют все точки обода
барабана, поэтому модуль его угловой
скорости ![]() .
Скорость точки касания колес 2 и 3
.
Скорость точки касания колес 2 и 3 ![]() ,
откуда определим модуль угловой скорости
шестерни 3
,
откуда определим модуль угловой скорости
шестерни 3
![]() ,
,
при t =
0,2 с: ![]()
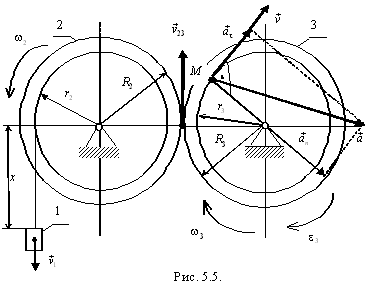
Модуль углового ускорения шестерни 3:
![]() .
.
Определим
модули скорости v,
касательного
,
нормального ![]() и
полного а ускорений
точки М:
и
полного а ускорений
точки М:
![]() =
10·0,08 = 0,8 м/с;
=
10·0,08 = 0,8 м/с; ![]() =
50·0,08 = 4 м/с2;
=
50·0,08 = 4 м/с2;
![]() =
102·0,08
= 8 м/с2;
=
102·0,08
= 8 м/с2; ![]() =
8,94 м/с2.
=
8,94 м/с2.
