Лекция 7. Плоское движение твердого тела

           

            7.1. Основные определения. Уравнения плоского движения

 

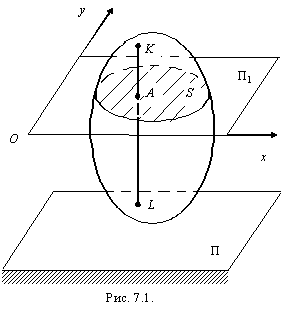
            Плоским или плоскопараллельным называют такое движение тела, при котором каждая его точка движется в плоскости, параллельной некоторой плоскости П, неподвижной в рассматриваемой системе отсчета (рис. 7.1). Из этого определения следует, что сечение S тела плоскостью   движется в плоскости  , а прямая KL, проведенная через точку Асечения перпендикулярно плоскости П, движется поступательно. Поэтому траектории, скорости и ускорения всех точек этой прямой одинаковы. Таким образом, плоское движение тела полностью определяется движением сечения S, в связи с чем в дальнейшем будем рассматривать движение плоской фигуры в плоскости  .

            Введем на плоскости   неподвижную систему координат xOy, тогда положение сечения S будет определяться координатами   точки А, называемой полюсом, и углом , образуемым отрезком АВ, который принадлежит сечению S, с положительным направлением оси Оx (рис. 7.2).

            Зависимости этих величин от времени

                             (7.1)

н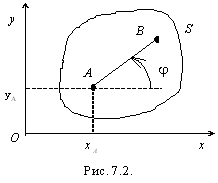 азывают уравнениями плоского движения твердого тела. Первые два из этих уравнений полностью определяют движение тела при неизменном угле , т.е. в случае его поступательного движения. Третье уравнение определяет движение тела, когда координаты точки А не изменяются, т.е. при вращении тела вокруг неподвижной оси, проходящей через полюс А перпендикулярно плоскости xOy.

            Так как в общем случае изменяются все три координаты, плоское движение тела можно представить как сумму двух движений: поступательного, определяемого движением полюса, и вращательного вокруг оси, проходящей через этот полюс и перпендикулярной плоскости движения. Характеристики поступательной части плоского движения (траектория, скорость и ускорение полюса) зависят от выбора полюса, так как в противном случае тело совершает поступательное движение. Характеристики вращательной части плоского движения (угловая скорость и угловое ускорение) от выбора полюса не зависят.

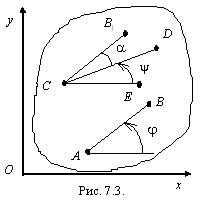             Действительно, выберем в качестве полюса точку С (рис. 7.3) и определим положение фигуры углом . Проведем отрезок  , тогда

,           (7.2)

где  = const.

            Продифференцируем равенство (7.2) по времени и получим

,

что и доказывает независимость вращательной части плоского движения от выбора полюса.

 

           

            7.2. Определение скоростей точек плоской фигуры

 

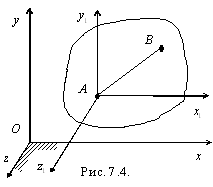             Введем подвижную систему координат , оси которой остаются параллельными осям неподвижной системы Oxyz (рис. 7.4). В данном случае подвижная система движется поступательно, а плоская фигура относительно нее вращается вокруг оси  . Точка В совершает сложное движение, ее абсолютная скорость

.                 (7.3)

Обозначим абсолютную скорость точки В как  , ее переносная скорость  , так как переносное движение поступательное, относительная скорость   равна скорости точки В при вращении плоской фигуры вокруг полюса А.

            Таким образом,

,                                             (7.4)

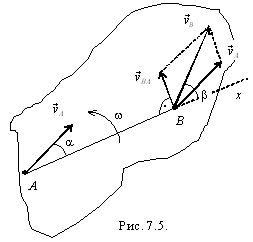
т.е. скорость произвольной точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки во вращательном движении фигуры вокруг полюса. Вращательная составляющая скорости   (рис. 7.5), ее модуль  .

 

            7.3. Теорема о проекциях скоростей

 

            Непосредственное использование зависимости (7.4) при определении скоростей точек не всегда целесообразно. Существуют другие соотношения, одно из которых даетследующая теорема: «Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны между собой».

            Для доказательства теоремы спроецируем векторное равенство (7.4) на ось х (см. рис. 7.5) и, учитывая, что  , получим

.                                            (7.5)

Формула (7.5) позволяет определить любую из четырех входящих в нее величин, если известны остальные три.

 

            7.4. Мгновенный центр скоростей

 

            Мгновенным центром скоростей (м.ц.с.) называют точку плоской фигуры, скорость которой в данный момент времени равна нулю.

            Докажем, что если угловая скорость плоской фигуры не равна нулю, то м.ц.с. существует и эта точка единственная. Пусть скорость точки А отлична от нуля  , т.е. она не является м.ц.с. (рис. 7.6). Проведем л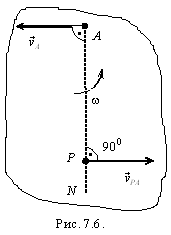 уч   в направлении вращения плоской фигуры и отложим на нем отрезок  . Выберем точку А за полюс и найдем скорость точки Р

,                     (7.6)

где  .

            Так как   и  ,   и из равенства (7.6) получим  , т.е. точка Р является м.ц.с.

            Предположим, что существует еще одна точка  , у которой скорость  . Однако в этом случае вся фигура в данный момент времени неподвижна и скорость точки А:  , что противоречит исходному предположению. Из этого противоречия следует единственность м.ц.с.

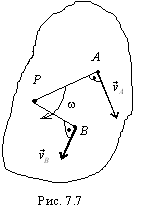
            Выберем в качестве полюса точку Р (рис. 7.7) и найдем скорости произвольных точек А и В фигуры:

;

,

т.е.  (см. рис. 7.7). Модули скоростей:

.                                 (7.7)

            Таким образом, скорости точек при плоском движении фигуры распределяются так же, как при вращательном движении вокруг оси, проходящей через м.ц.с. перпендикулярно плоскости движения. Иными словами, скорости перпендикулярны отрезкам, соединяющим точки с м.ц.с., а модули скоростей пропорциональны расстояниям от точек до м.ц.с. Из равенств (7.7) следует, что угловая скорость фигуры в данный момент времени равна отношению скорости какой-либо точки фигуры к расстоянию от этой точки до м.ц.с.

.                           (7.8)

Зная положение м.ц.с. и скорость некоторой точки фигуры, можно, используя соотношения (7.7) и (7.8), определить скорость любой другой ее точки.

 

 

            7.5. Определение положения мгновенного центра скоростей

 

            Рассмотрим типичные ситуации, в которых можно определить положение м.ц.с.

            7.5.1. Пусть известны скорость некоторой точки фигуры и ее угловая скорость. Такой случай уже рассмотрен при доказательстве существования м.ц.с.

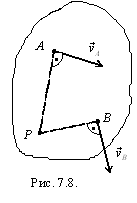
            7.5.2. Пусть известны направления скоростей двух точек фигуры и эти скорости не параллельны (рис. 7.8). Из предыдущего следует, что м.ц.с. находится в точке пересечения перпендикуляров к скоростям  , проведенных из точек А и В.

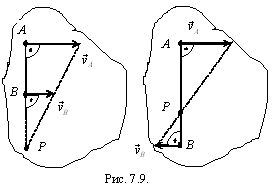
            7.5.3. Пусть скорости двух точек фигуры параллельны друг другу, перпендикулярны отрезку, соединяющему точки, и не равны по модулю. Так как модули скоростей пропорциональны расстояниям от точек до м.ц.с., то для определения его положения произведем построения, показанные на рис. 7.9.

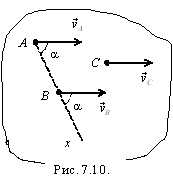
            7.5.4. Пусть скорости двух точек фигуры параллельны друг другу  и не перпендикулярны отрезку, соединяющему точки (рис. 7.10). Из теоремы о проекциях скоростей следует, что  , т.е. модули скоростей равны ( ) и, следовательно,  . Тогда из выражения (7.4) получим, что  , т.е. угловая скорость плоской фигуры = 0.Скорость произвольной точки С:  , так как  . Следовательно, в данный момент времени скорости всех точек фигуры одинаковы, а ее угловая скорость равна нулю. Такое движение тела называют мгновенно поступательным.

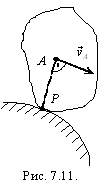
            7.5.5. Если одно тело катится без скольжения по неподвижной поверхности другого тела (рис. 7.11), то м.ц.с. находится в точке соприкосновения тел, так как при отсутствии скольжения скорость этой точки подвижного тела равна нулю.

           

            7.6. Определение ускорений точек плоской фигуры

 

            Используем введенную в подразделе 7.2 подвижную систему координат   (см. рис. 7.4) и рассмотрим движение точки В как сложное. Поскольку переносное движение является поступательным, абсолютное ускорение точки В определим по формуле (6.13)

.Обозначим абсолютное ускорение точки В  , ее переносное ускорение  , так как переносное движение поступательное, относительное ускорение   имеет касательную и нормальную составляющие:

,  .

Модули этих составляющих:

.                                   (7.9)

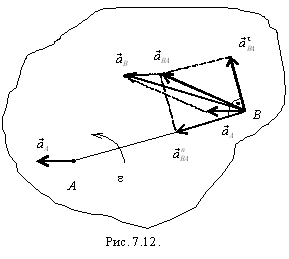
            Таким образом, ускорение произвольной точки плоской фигуры равно геометрической сумме ускорения полюса, касательного и нормального ускорений точки во вращательном движении фигуры относительно полюса

.                                         (7.10)

На рис. 7.12 показано геометрическое определение вектора   по формуле (7.10).

            Пример. Кривошипно-шатунный механизм приводится в движение кривошипом ОА, который вращается с постоянной угловой скоростью  . Колесо катится без скольжения (рис. 7.13).

            Определить для заданного положения механизма скорости точек А, В, С и D, угловые скорости и угловые ускорения шатуна АВ и колеса, ускорение точки В, если ОА = АС = СВ = b, R = b/2.

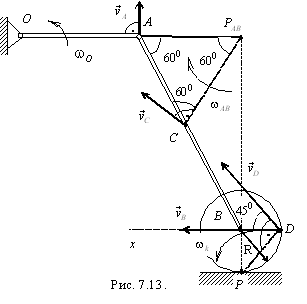
            Кривошип ОА вращается вокруг неподвижной оси О, шатун АВ и колесо совершают плоское движение. Модуль скорости точки А

Скорость   направлена горизонтально. Проведем из точек А и В перпендикуляры к скоростям   и получим в точке их пересечения   м.ц.с. шатуна АВ,   (см. рис. 7.13).

            Поскольку  , то   –равносторонний и  . Угловая скорость шатуна АВ

.

Модули скоростей точек В и С:

;

.

            Так как колесо катится без скольжения, его м.ц.с. находится в точке Р, где колесо касается неподвижной поверхности,  . Угловая скорость колеса

.

Скорость точки D определим по теореме о проекциях скоростей. Проецируя скорости   и   на ось Dx, получим

.

            Выберем точку А за полюс и найдем ускорение точки В по формуле (7.10). Ускорение точки А имеет только нормальную составляющую, так как кривошип вращается равномерно:

;

;

.

            Ускорение   точки В направлено горизонтально (рис. 7.14). Спроецируем равенство (7.10) на оси Bx, By:

;                         (7.11)

.                                 (7.12)

            Далее получим:

            – из уравнения (7.12)    ,

            – из уравнения (7.11)    .

            Угловое ускорение шатуна АВ

.

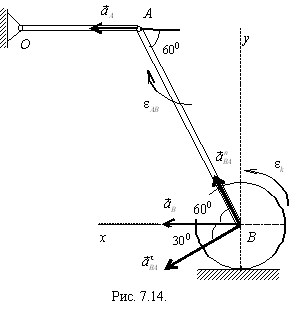
            Угловое ускорение колеса получим дифференцированием по времени соотношения

,

определяющего его угловую скорость,

.