2.4. Условия равновесия системы пар сил
Поскольку систему пар сил, действующих на твердое тело, всегда можно привести к одной паре, для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары был равен нулю. Тогда из формулы (2.10) получим
.
(2.11)
Действительно, в этом случае либо силы результирующей пары равны нулю, либо плечо пары равно нулю. Если имеет место последнее, силы пары направлены вдоль одной прямой и в соответствии с 1-й аксиомой статики уравновешены. Проецируя векторное уравнение (2.11) на координатные оси, получим три скалярных уравнения:
.
(2.12)
Вопросы для самоконтроля
1. Дайте определение момента силы относительно точки.
2. Как определить момент силы относительно оси?
3. Какую систему сил называют парой сил? Как определить ее момент?
4. Какие преобразования пары сил не изменяют ее действие на твердое тело?
5. Каковы условия равновесия системы пар сил?
Лекция 3. Основная теорема статики и условия равновесия пространственной системы сил
3.1. Лемма о параллельном переносе силы
Следствие из аксиомы 2 устанавливает, что при переносе точки приложения силы вдоль линии ее действия получаем силу, эквивалентную исходной. Рассматриваемая лемма показывает, как можно перенести силу в любую точку, не изменяя ее действие на тело.
Лемма. Действие силы на твердое тело не изменится, если ее приложить в любой другой точке тела и добавить пару сил, момент которой равен моменту данной силы относительно новой точки ее приложения.
Доказательство
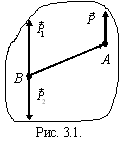
Рассмотрим
силу
,
приложенную в точке A (рис.
3.1). В произвольной точке B приложим
уравновешенную систему сил 
0,
где 
, 
,
тогда на основании аксиомы 2 получим,
что 
,
где силы 
образуют
пару сил, момент которой
.
Лемма доказана.
3.2. Основная теорема статики
Для произвольной системы сил введем два определения.
Главным вектором системы сил называют величину, равную сумме всех сил системы,
(3.1)
Главным моментом системы сил относительно некоторого центра О называют величину, равную сумме моментов всех сил системы относительно центра,
.
(3.2)
Основная теорема статики (теорема Пуансо). Произвольная пространственная система сил эквивалентна силе, равной главному вектору системы и приложенной в некоторой точке (центре приведения), и паре сил, момент которой равен главному моменту системы относительно выбранного центра приведения.
Доказательство
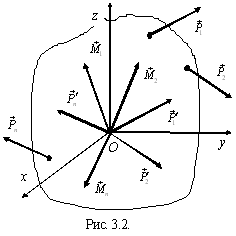Рассмотрим
систему сил
,
показанную на рис. 3.2. Используем
доказанную лемму и перенесем все силы
в центр приведения O,
добавляя соответствующие пары сил.
В результате получим:
– систему
сходящихся сил 
,
где 
;
– систему
пар сил, моменты которых 
,
где 
.
Систему сходящихся сил заменим ее равнодействующей
,
равной главному вектору исходной системы, а систему пар сил – одной парой, момент которой
равен главному моменту исходной системы относительно центра O.
Теорема доказана.
Следствие. Две системы сил эквивалентны тогда и только тогда, когда они имеют одинаковые главные векторы и одинаковые главные моменты относительно одного и того же центра.
|
Рис.
3.3.
(рис.
3.3). Сила 
не
зависит от выбора центра приведения и
равна сумме всех сил системы, т.е.
.
Определим главный момент системы относительно нового центра
где 
.
Таким образом,
,
(3.3)
т.е. при изменении центра приведения главный момент изменяется на величину момента силы, равной главному вектору и приложенной в первоначальном центре приведения, относительно нового центра приведения.
Предположим,
что для некоторого центра O: 
и 
.
Тогда вследствие формулы (3.3) для любого
центра
: 
и 
.