4.5. Частные случаи движения точки

 

            4.5.1. Равномерное движение точки. Это движение с постоянной алгебраической скоростью, т.е.   = const. Касательное ускорение  , а нормальное ускорение обращается в нуль только при прямолинейном равномерном движении или в точках перегиба траектории при криволинейном движении.

            Закон изменения координаты S получим из соотношения

= const,

откуда                                     ,

где   – значение координаты S в начальный момент времени t = 0.

            4.5.2. Равнопеременное движение точки. Это движение с постоянным по модулю касательным ускорением:  = const.

            Законы изменения алгебраической скорости и координаты получим, интегрируя следующие соотношения:

= const,   откуда  ,

   откуда  ,

где   – начальные значения алгебраической скорости и координаты.

            Пример. Движение точки M задано координатным способом:

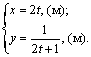                                            (4.26)

            Определить траекторию точки, а также ее скорость, ускорение и радиус кривизны траектории в момент времени  = 0,5 с.

            Чтобы записать уравнение движения точки M в координатной форме, исключим из уравнений (4.26) время t. Из 1-го уравнения (4.26) получим 2t = x и подставим во 2-е уравнение:  , т.е. точка движется по гиперболе. Считая, что t  0, в качестве траектории будем иметь участок ветви гиперболы, для точек которого x  0 (рис. 4.8, сплошная линия). При  = 0,5 с: x = 1 м, y = 0,5 м.

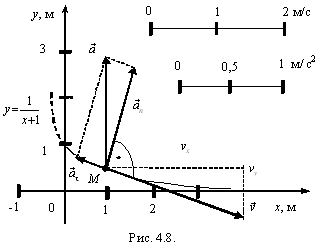
            Определим проекции скорости точки:

= 2 м/с;   = – 0,5 м/с.

Модуль скорости:

= 2,06 м/с.

Проекции ускорения точки:

;         = 1 м/с².

Модуль ускорения:

= 1 м/с².

            Определим касательное ускорение точки M как проекцию вектора ускорения на направлении вектора скорости

= – 0,24 м/с².

Так как  , вектор   направлен по касательной к траектории в сторону, противоположную вектору скорости  .

            Нормальное ускорение:

= 0,97 м/с².

Вектор нормального ускорения направлен по нормали к траектории в сторону вогнутости.

            Теперь определим из формулы (4.24) радиус кривизны траектории

= 4,38 м.

 

 

Лекция 5. Простейшие движения твердого тела

 

            В кинематике рассматривают идеализированные недеформируемые тела, которые называют абсолютно твердыми или просто твердыми. Расстояние между любыми двумя точками такого тела остается неизменным и не зависит от действующих на него сил.

            Простейшие движения твердого тела – поступательное и вращательное. Более сложные движения могут быть представлены как совокупность простейших.

 

5.1. Поступательное движение твердого тела

 

            Поступательным называют такое движение твердого тела, при котором прямая, соединяющая две любые точки этого тела, перемещается, оставаясь параллельной своему начальному направлению.

            Свойства поступательного движения твердого тела определяют следующей теоремой: «При поступательном движении твердого тела все его точки описывают одинаковые (совпадающие при наложении) траектории и имеют в каждый момент времени одинаковые скорости и ускорения».

Доказательство

            Пусть тело движется поступательно относительно координатной системы Oxyz (рис. 5.1). Радиусы-векторы произвольных точек А и В связаны между собой соотношением

.                                                (5.1)

Модуль вектора   как расстояние между двумя точками твердого тела не изменяется и его направление остается неизменным, так как тело движется поступательно. Следовательно, вектор = const и траектория точки В может быть получена из траектории точки А параллельным смещением, т.е. при наложении траектории этих точек совпадают.

            Продифференцируем соотношение (5.1) по времени и получим

,

где  . Поэтому   или  . Дифференцируя последнее соотношение по времени, запишем

 или  ,

что и доказывает утверждение теоремы. Из нее следует, что изучение поступательного движения тела сводится к уже рассмотренной задаче кинематики точки.