
- •Статика Лекция 1. Основные понятия и аксиомы статики. Система сходящихся сил
- •1.1. Основные понятия статики
- •1.2. Аксиомы статики
- •1.3. Связи и их реакции
- •1.4. Система сходящихся сил
- •1.5. Условия равновесия системы сходящихся сил
- •1.6. Решение задач статики
- •Лекция 2. Теория пар
- •2.1. Момент силы относительно точки и оси
- •2.2. Пара сил и ее момент
- •2.3. Теоремы о парах
- •2.4. Условия равновесия системы пар сил
- •Вопросы для самоконтроля
- •Лекция 3. Основная теорема статики и условия равновесия пространственной системы сил
- •3.1. Лемма о параллельном переносе силы
- •3.2. Основная теорема статики
- •3.3. Приведение системы сил к двум силам
- •3.4. Условия равновесия пространственной системы сил
- •3.5. Теорема Вариньона
- •3.6. Условия равновесия плоской системы сил
- •Кинематика Лекция 4. Кинематика точки
- •4.1. Некоторые определения
- •4.2. Способы задания движения точки
- •4.3. Определение скорости точки
- •4.4. Определение ускорения точки
- •4.5. Частные случаи движения точки
- •Лекция 5. Простейшие движения твердого тела
- •5.1. Поступательное движение твердого тела
- •5.2. Вращение твердого тела вокруг неподвижной оси
- •5.3. Угловая скорость твердого тела
- •5.4. Угловое ускорение твердого тела
- •5.5. Частные случаи вращательного движения
- •5.6. Скорость и ускорение точки тела, вращающегося вокруг
- •Лекция 6. Сложное движение точки
- •6.1. Основные определения
- •6.2. Определение абсолютной скорости точки
- •6.3. Определение абсолютного ускорения точки
- •Лекция 7. Плоское движение твердого тела
6.3. Определение абсолютного ускорения точки
Рассмотрим случай переносного вращательного движения и запишем формулу (6.5) в виде:
![]() .
(6.6)
.
(6.6)
Продифференцируем соотношение (6.6) по времени
![]()
![]() .
(6.7)
.
(6.7)
Здесь ![]() –
абсолютное ускорение точки М;
–
абсолютное ускорение точки М;
![]() –
вектор
углового ускорения подвижной системы
координат;
–
вектор
углового ускорения подвижной системы
координат; ![]() ;
; ![]() ;
; ![]() ;
; ![]() –
относительное ускорение точки М;
–
относительное ускорение точки М;
![]() .
.
Теперь из формулы (6.7) получим
![]()
![]() .
(6.8)
.
(6.8)
Первые
два слагаемых этого равенства представляют
собой в соответствии с выражением (5.22)
ускорение точки подвижной системы
координат, совпадающей с движущейся
точкойМ,
т.е. являются ее переносным ускорением ![]() .
Последнее слагаемое называют кориолисовым
ускорением
.
Последнее слагаемое называют кориолисовым
ускорением
![]() .
(6.9)
.
(6.9)
К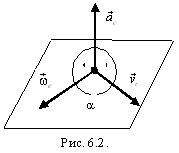 ориолисово
ускорение направлено перпендикулярно
плоскости, в которой лежат векторы
и
,
в ту сторону, откуда поворот вектора
к
вектору
на
наименьший угол виден против часовой
стрелки (рис. 6.2).
ориолисово
ускорение направлено перпендикулярно
плоскости, в которой лежат векторы
и
,
в ту сторону, откуда поворот вектора
к
вектору
на
наименьший угол виден против часовой
стрелки (рис. 6.2).
Модуль кориолисова ускорения:
![]() ,
(6.10)
,
(6.10)
где – угол между векторами и .
Для
определения модуля и направления
кориолисова ускорения можно
использовать правило
Жуковского:
«Для
построения вектора кориолисова
ускорения ![]() надо
спроецировать вектор
на
плоскость, перпендикулярную
вектору
, умножить
полученную проекцию
надо
спроецировать вектор
на
плоскость, перпендикулярную
вектору
, умножить
полученную проекцию ![]() на
на ![]() и
повернуть полученный вектор на
и
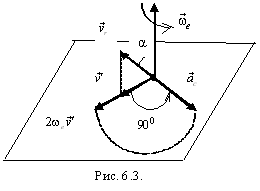
повернуть полученный вектор на ![]() вокруг
вектора
в
сторону переносного вращения»
(рис. 6.3). Легко проверить, что направление
полученного вектора совпадает с
направлением вектора
,
определенным по формуле (6.9), его модуль
вокруг
вектора
в
сторону переносного вращения»
(рис. 6.3). Легко проверить, что направление
полученного вектора совпадает с
направлением вектора
,
определенным по формуле (6.9), его модуль![]() .
.
 Кориолисово
ускорение равно нулю в следующих случаях:
Кориолисово
ускорение равно нулю в следующих случаях:
1)
в те моменты времени, когда относительная
скорость равна нулю ![]() ;
;
2)
если векторы
и
коллинеарны,
т.е. угол между ними =
0 или ![]() ;
;
3)
в те моменты времени, когда угловая
скорость переносного движения равна
нулю ![]() .
.
Итак, из уравнения (6.8) получим
![]() .
(6.11)
.
(6.11)
Этот результат выражает содержание теоремы Кориолиса: «Абсолютное ускорение точки в случае переносного вращательного движения равно геометрической сумме переносного, относительного и кориолисова ускорений».
В общем случае переносное и относительное ускорения могут быть представлены в виде сумм касательных и нормальных составляющих, и тогда формула (6.11) примет вид:
![]() .
(6.12)
.
(6.12)
Рассмотрим случай переносного поступательного движения. Запишем формулу (6.5) так:
![]()
![]()
и
продифференцируем ее по времени,
учитывая, что при поступательном
переносном движении ![]() :
:
![]() ,
,
где
![]() ;
;
![]() –
абсолютное,
переносное и относительное ускорения
точки М.
–
абсолютное,
переносное и относительное ускорения
точки М.
Таким образом, при переносном поступательном движении абсолютное ускорение точки равно геометрической сумме переносного и относительного ускорений:
![]() .
(6.13)
.
(6.13)
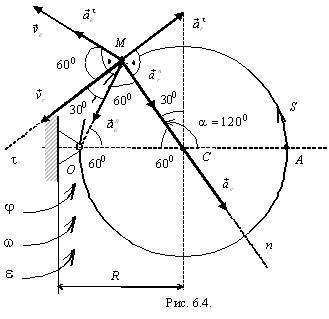
Пример. Круглая
пластина радиусом R =
60 см вращается вокруг неподвижной оси,
перпендикулярной плоскости пластины
и проходящей через точку О,
лежащую на ее ободе, по закону ![]() рад
(рис. 6.4). По ободу пластины движется
точка М,
положение которой определяется
координатой
рад
(рис. 6.4). По ободу пластины движется
точка М,
положение которой определяется
координатой ![]() см.
см.
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1 с.
Положение точки М в заданный момент времени определим с помощью центрального угла
![]() рад
=
рад
= ![]() .
.
Найдем
угловую скорость ![]() и
угловое ускорение
и
угловое ускорение![]() пластины:
пластины:
![]() 4
рад/с;
4
рад/с;
![]() 8
рад/c2 = const,
8
рад/c2 = const,
а также их модули:
![]() .
.
Так
как ![]() и
и ![]() ,
пластина вращается в сторону увеличения
угла ускоренно.
Треугольник ОСМ равносторонний,
поэтому ОМ = R =
60 см. Абсолютная скорость точки М:
,
пластина вращается в сторону увеличения
угла ускоренно.
Треугольник ОСМ равносторонний,
поэтому ОМ = R =
60 см. Абсолютная скорость точки М: ![]() .
Проекция относительной скорости на
касательную М
.
Проекция относительной скорости на
касательную М
![]() см/с.
см/с.
Модуль относительной скорости
![]() 125,66
см/с.
125,66
см/с.
Модуль переносной скорости
![]() см/с;
см/с; ![]() .
.
Модуль абсолютной скорости точки М:
![]() =
=
![]() =
321,8 см/с.
=
321,8 см/с.
Абсолютное ускорение точки М
![]() .
.
Проекция относительного касательного ускорения на ось М:
![]() –
251,32
см/с2,
–
251,32
см/с2,
его модуль
![]() =
251,32 см/с2.
=
251,32 см/с2.
Модуль относительного нормального ускорения
![]() =
263,17 см/с2.
=
263,17 см/с2.
Модули переносного касательного и нормального ускорений:
![]() см/с2;
см/с2; ![]() ;
;
![]() см/с2;
см/с2; ![]() .
.
Направление
вектора кориолисова ускорения ![]() получим
по правилу Жуковского, повернув вектор
относительной скорости
на
получим
по правилу Жуковского, повернув вектор
относительной скорости
на ![]() в
направлении вращения пластины. Вектор
угловой скорости переносного
движения
направлен
вдоль оси вращения, поэтому
в
направлении вращения пластины. Вектор
угловой скорости переносного
движения
направлен
вдоль оси вращения, поэтому ![]() и
модуль кориолисова ускорения найдем
так:
и
модуль кориолисова ускорения найдем
так:
![]() см/с2.
см/с2.
Определим проекции абсолютного ускорения на оси M и Mn, для чего спроецируем на них векторное равенство (6.14),
![]()
![]() см/с2;
см/с2;
![]()
![]() см/с2.
см/с2.
Модуль абсолютного ускорения точки М:
![]() см/с2.
см/с2.
