4.2. Основные теоремы двойственности

ТЕОРЕМА 1. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причём для любых оптимальных решений и выполняется равенство

.

Если одна из двойственных задач неразрешима ввиду того, что (или ), то другая задача не имеет допустимых решений.

ТЕОРЕМА 2. Для оптимальности допустимых решений и пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений

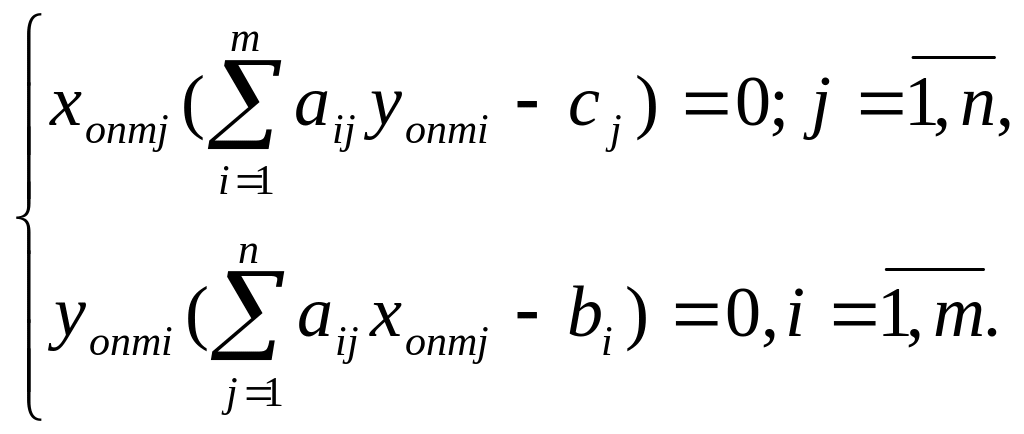
Теоремы позволяют определить оптимальное решение одной из пары задач по решению другой.

Лекция 5

4.3. Решение двойственных задач

Решение симметричных задач

Рассмотрим решение задач с использованием теорем двойственности.

Исходная задача

при ограничениях:

Двойственная задача

при ограничениях:

Решим исходную задачу графическим методом, получим , при этом

На основании 1-й теоремы двойственности

Так как , >0, то по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств:

Подставим в систему ограничений исходной задачи:

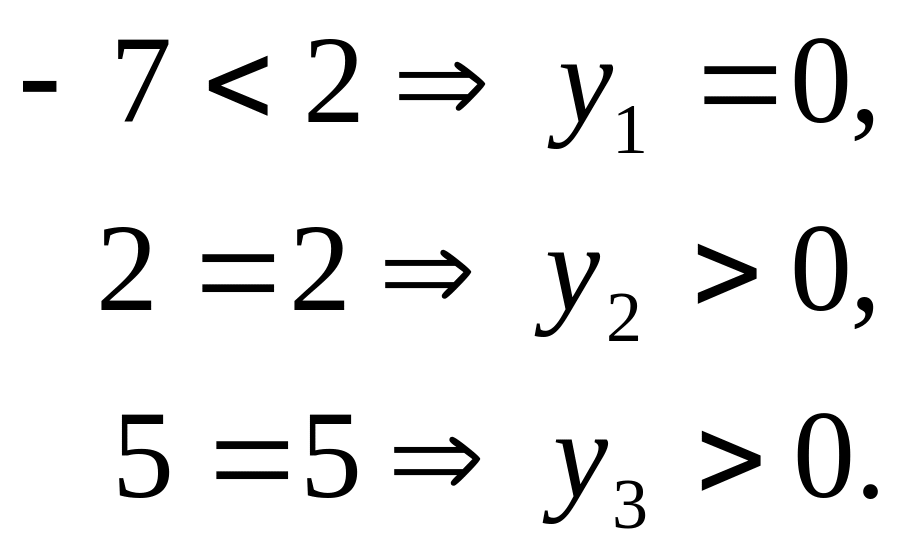
Тогда система ограничений двойственной задачи примет вид

Откуда , при этом

Пусть дано решение двойственной задачи , , найдём решение исходной.

По 1-й теореме двойственности Так как , > 0, то по 2-й теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства:

Откуда , при этом

Рассмотрим решение задач методом, основанным на взаимно однозначном соответствии между переменными: основным переменным исходной задачи соответствуют балансовые переменные двойственной, и наоборот. Для этого решим двойственную задачу симплексным методом:

при ограничениях:

Из табл. 4.1 следует, что , .

Таблица 4.1

bj	БП	2	2	5	0	0
		y1	y2	y3	y4	y5	cj
		-2 1	1 -2	1 1	-1 0	0 -1	1 -1

bj	БП	2	2	5	0	0
		y1	y2	y3	y4	y5	cj
2	y2	-2 -3	1 0	1 3	-1 -2	0 -1	1 1

bj	БП	2	2	5	0	0
		y1	y2	y3	y4	y5	cj
2 5	y2 y3	-1 -1	1 0	0 1	-1/3 -2/3	1/3 -1/3	2/3 1/3
∆i		-9	0	0	-4	-1	3

На основании 1-й теоремы двойственности получаем

Решение другой задачи найдём по соответствию между переменными:

	Основные переменные	Балансовые переменные
Исходная задача	x1 x2	x3 x4 x5
Двойственная	y4 y5	y1 y2 y3
	Балансовые переменные	Основные переменные

Значение x_j определяем по последней симплексной таблице в строке ∆_i в соответствующем столбце, причём значения x_j берутся по модулю:.

Таким образом, решение двойственной задачи:

, .

Если исходная задача решена симплексным методом, то решение двойственной задачи может быть найдено по формуле где С – матрица-строка коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи; А^-1 – обратная матрица для матрицы А, являющейся матрицей коэффициентов системы ограничений исходной задачи для базисных переменных в оптимальном решении.

Решим симплексным методом исходную задачу вида

при ограничениях:

Таблица 4.2

сi	БП	1	-1	0	0	0
		х1	х2	х3	х4	х5	bi
0 0 0	x3 x4 x5	-2 1 1	1 -2 1	1 0 0	0 1 0	0 0 1	2 2 5
∆j		-1	1	0	0	0	0

сi	БП	1	-1	0	0	0
		х1	х2	х3	х4	х5	bi
0 1 0	x3 x1 x5	0 1 0	-3 -2 3	1 0 0	2 1 -1	0 0 1	6 2 3
∆j		0	-1	0	1	0	2

сi	БП	1	-1	0	0	0
		х1	х2	х3	х4	х5	bi
0 1 -1	x3 x1 x2	0 1 0	0 0 1	1 0 0	1 1/3 -1/3	1 2/3 1/3	9 4 1
∆j		0	0	0	2/3	1/3	3

Из табл. 4.2 следует, что , при этом

Матрицы записываются в виде

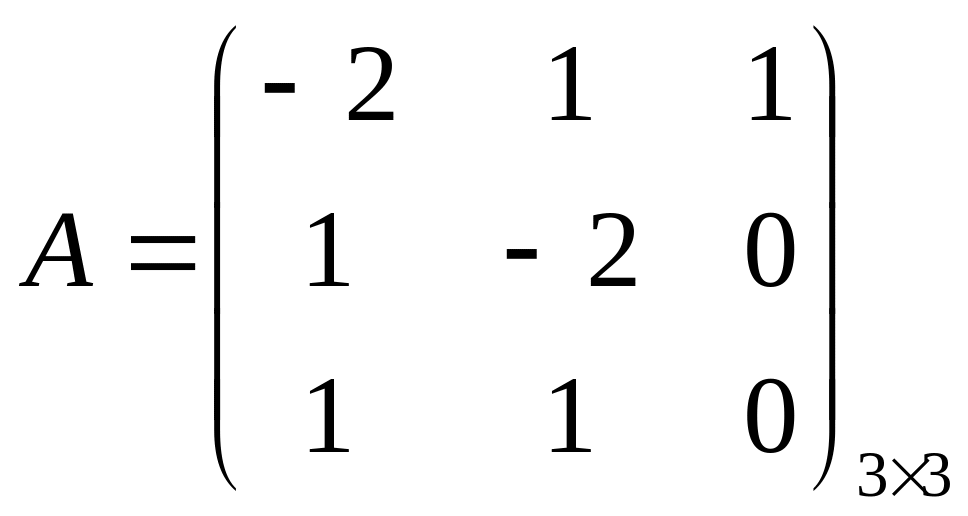, , тогда .

= .

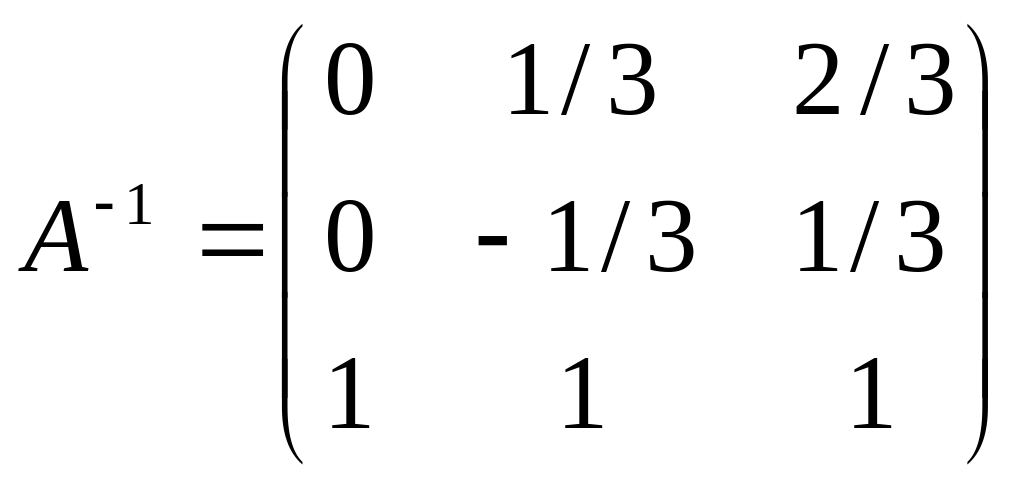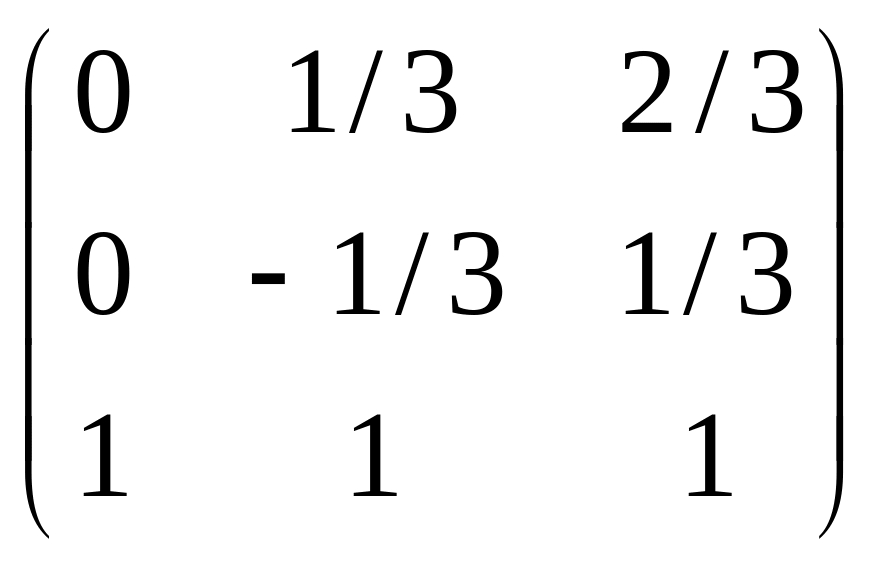Таким образом, решение двойственной задачи следующее:

, при этом .

Решение несимметричных задач

Рассмотрим решение задач с использованием теорем двойственности.