3.4. Альтернативный оптимум

Критерием альтернативного оптимума при решении задач симплексным методом является равенство нулю хотя бы одной оценки свободной переменной

Если оценка свободной переменной равна нулю, то решение находится по формуле

,

где

Пример. Дана задача линейного программирования

при ограничениях:

РЕШЕНИЕ. Составим симплексную таблицу (табл. 3.6).

Таблица 3.6

ci	БП	0	2	-4	0	2
		x1	x2	x3	x4	x5	bi
0 0	x1 x4	1 0	3 -2	-1 4	0 1	2 0	7 12
		0	-2	4	0	-2	0

В индексной строке имеется одна положительная оценка. Полученное решение можно улучшить. Ключевым элементом является 4. Составляем симплексную таблицу 2-го шага (табл. 3.7).

Таблица 3.7

ci	БП	0	2	-4	0	2
		x1	x2	x3	x4	x5	bi
0 -4	x1 x3	1 0	5/2 -1/2	0 1	1/4 1/4	2 1/2	10 3
		0	0	0	-1	-2	-12

Получаем

Так как , то задача имеет альтернативный оптимум. Найдём ещё одно оптимальное решение, введя вместо базисной переменной х₁ свободную переменную х₂ (табл. 3.8).

Таблица 3.8

ci	БП	0	2	-4	0	2
		x1	x2	x3	x4	x5	bi
2 -4	х2 x3	2/5 1/5	1 0	0 1	1/10 3/10	4/5 9/10	4 5
		0	0	0	-1	-4	-12

Получаем

Найдём координаты оптимального решения задачи:

Давая t значения из [0, 1], получим различные , при которых

Лекция 4

4. Двойственность в линейном программировании

Произвольную задачу линейного программирования можно определённым образом сопоставить с другой задачей линейного программирования, называемой двойственной.

4.1. Виды двойственных задач и составление их математических моделей

Симметричные двойственные задачи

Дана исходная задача

при ограничениях:

Задача дана в неканоническом виде. Составим математическую модель двойственной задачи, для этого:

• каждому неравенству системы ограничений исходной задачи приводим в соответствие переменную y_i;

• составляем целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи. Функция стремится к минимуму, если в исходной задаче целевая функция стремилась к максимуму, и наоборот;

• составляем систему ограничений. Коэффициенты системы ограничений образуют транспонированную матрицу коэффициентов системы ограничений исходной задачи. Знаки неравенств зависят от целевой функции: если она в двойственной задаче стремится к минимуму, то знаки неравенств « 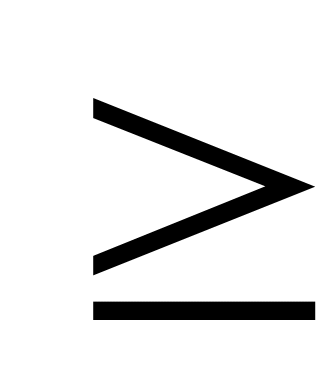», и наоборот;

• свободными членами системы ограничений являются коэффициенты целевой функции исходной задачи. Все переменные двойственной задачи неотрицательные.

Математическая модель двойственной задачи имеет вид

при ограничениях:

Несимметричные двойственные задачи

Дана исходная задача

при ограничениях:

Задача дана в каноническом виде. Составим математическую модель двойственной задачи.

Для её составления пользуются тем же правилом, что и при составлении симметричной задачи, с учётом следующих особенностей:

• ограничениями двойственной задачи будут неравенства. Если в целевой функции двойственной задачи требуется найти минимум, то знак неравенства , если максимум, то ;

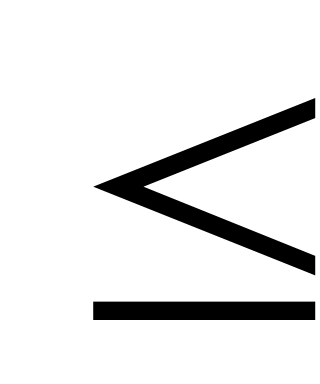• переменные y_i – произвольные по знаку

Математическая модель двойственной задачи имеет вид

при ограничениях:

y_i – произвольные по знаку,

Смешанные двойственные задачи

Математическая модель исходной задачи имеет условия симметричных и несимметричных задач. При составлении двойственной задачи необходимо выполнять правила симметричных и несимметричных задач: та переменная, которая соответствует равенству в исходной задаче, может быть произвольного знака в двойственной задаче, а та переменная, которая соответствует неравенству, должна быть в двойственной задаче неотрицательной.