
- •Глава I элементы линейного программирования Лекция 1
- •1. Элементы аналитической геометрии
- •1.1. Основные понятия и определения
- •1.2. Решение систем т линейных уравнений с двумя переменными
- •Лекция 2
- •2. Графический метод
- •2.1. Постановка задачи
- •2.2. Алгоритм решения задач
- •2.3. Выбор оптимального варианта выпуска изделий
- •Лекция 3
- •3. Симплексный метод
- •3.1. Общая постановка задачи
- •3.2. Алгоритм симплексного метода
- •Лекция 3.
- •3.3. Анализ эффективности использования производственного потенциала предприятия
- •3.4. Альтернативный оптимум
- •Лекция 4
- •4. Двойственность в линейном программировании
- •4.1. Виды двойственных задач и составление их математических моделей
- •4.2. Основные теоремы двойственности
- •Исходная задача
- •Двойственная задача
- •Исходная задача
- •Двойственная задача
- •Лекция 6
- •5. Транспортная задача
- •5.1. Общая постановка задачи
- •5.2. Нахождение исходного опорного решения
- •5.3. Определение эффективного варианта доставки изделий к потребителю
- •5.4. Проверка найденного опорного решения на оптимальность
- •5.5. Переход от одного опорного решения к другому
- •5.6. Альтернативный оптимум в транспортных задачах
- •Вырожденность в транспортных задачах
- •Открытая транспортная задача
- •Определение оптимального варианта перевозки грузов
- •Приложение транспортных моделей к решению некоторых экономических задач.
- •Выбор оптимального варианта использования производственного оборудования
- •Лекция 10 Целочисленное программирование
- •Параметрическое программирование
- •1. Постановка задачи
- •2. Линейное программирование с параметром в целевой функции
- •Определение диапазона оптимального решения выпуска продукции при изменении условий реализации
- •Транспортная параметрическая задача
- •Лекция Задача о назначениях
- •Нелинейное программирование Общая постановка задачи
- •Графический метод
- •Дробно-линейное программирование
- •Алгоритм решения
- •Экономическая интерпретация задач дробно-линейного программирования
- •Применение дробно-линейного программирования для определения себестоимости изделий
- •Сведение экономико-математической модели дробно-линейного программирования к задаче линейного программирования
- •Метод множителей Лагранжа
- •Динамическое программирование
- •Оптимальная стратегия замены оборудования
- •Сетевые модели
- •Выбор оптимальной стратегии развития предприятия в условиях трансформации рынка
- •Принятие решения о замене оборудования в условиях неопределённости и риска
- •Элементы системы массового обслуживания (смо)
- •1. Формулировка задачи и характеристики смо
- •2. Смо с отказами
- •3. Смо с неограниченным ожиданием
- •4. Смо с ожиданием и с ограниченной длиной очереди
Лекция Задача о назначениях
Задача заключается в выборе такого распределения ресурсов по объектам, при котором минимизируется стоимость назначений. Предполагается, что каждый ресурс назначается ровно один раз и каждому объекту приписывается ровно один ресурс.
Матрица стоимостей
С имеет
вид С = (сij),
где сij
– затраты, связанные с назначением
i-го
ресурса на j-й
объект, i
= j
=
![]() ,
где п
– число объектов или ресурсов.
,
где п
– число объектов или ресурсов.
Обозначим:
если i-й ресурс назначается
на j-й объект;
в противном случае.
![]()
Таким образом, решение задачи может быть записано в виде X = (xij).
Допустимое решение называется назначением. Оно строится путём выбора ровно одного элемента в каждой строке матрицы X = (xij) и ровно одного элемента в каждом столбце этой матрицы.
Элементы сij матрицы С, соответствующие элементам xij = 1 матрицы Х будем отмечать кружками:
С = (сij)
=
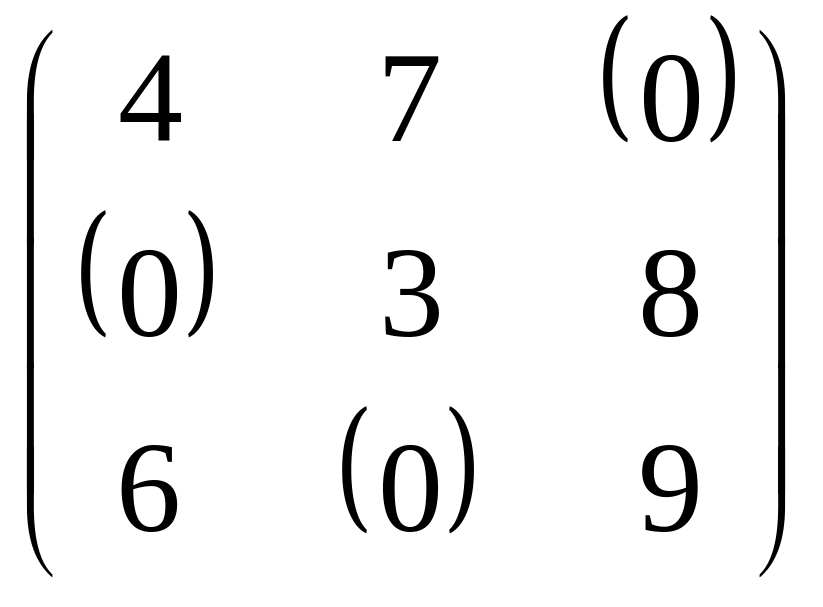 , X
= (xij)
=
, X
= (xij)
=
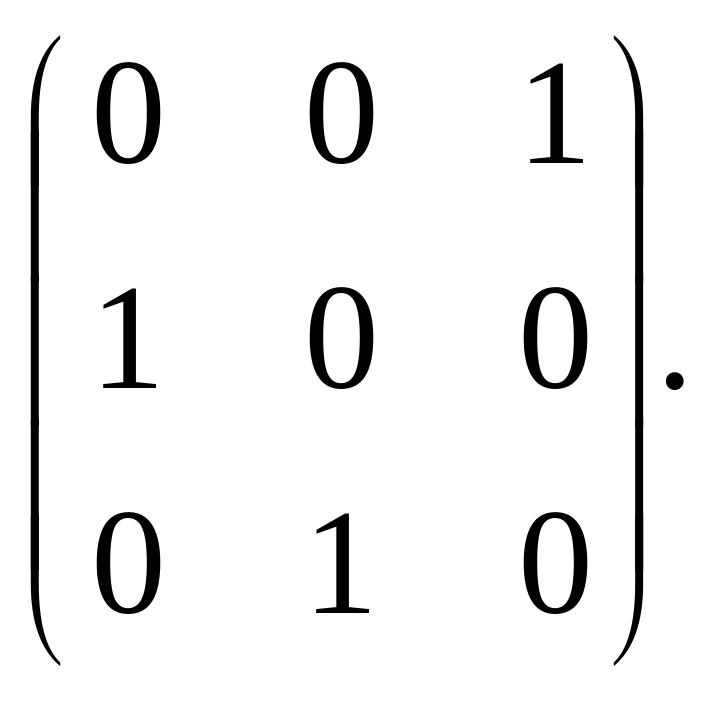
Математическая постановка задачи:
![]()
при ограничениях:
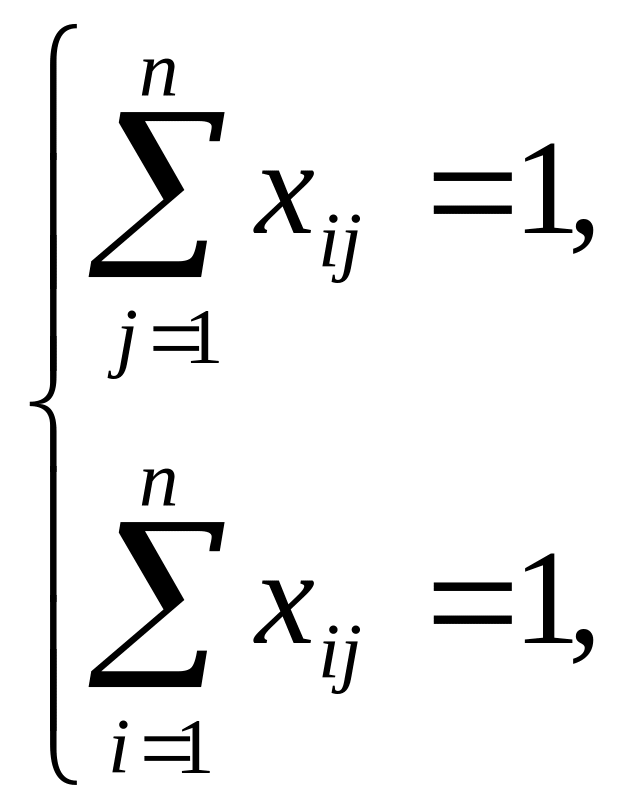
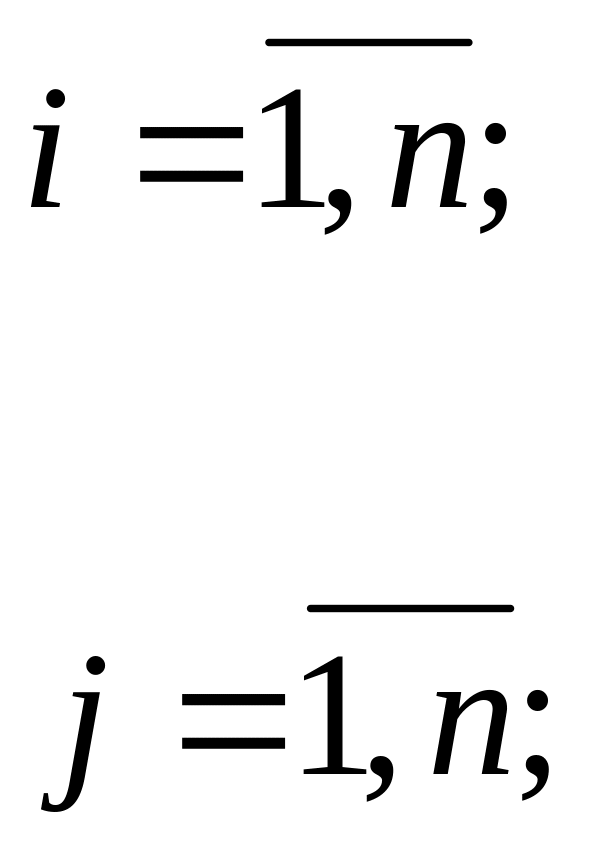
xij = 0 или 1.
Алгоритм решения задачи
Рассмотрим метод, называемый венгерским алгоритмом. Он состоит из следующих шагов:
преобразование строк и столбцов матрицы;
определение назначения;
модификация преобразованной матрицы.
1-й шаг. Цель данного шага – получение максимально возможного числа нулевых элементов в матрице С. Для этого из всех элементов каждой строки вычитаем минимальный элемент соответствующей строки, а из всех элементов каждого столбца вычитаем минимальный элемент соответствующего столбца..
2-й шаг. Если после выполнения 1-го шага в каждой строке и каждом столбце матрицы С можно выбрать по одному нулевому элементу, то полученное решение будет оптимальным назначением.
3-й шаг. Если допустимое решение, состоящее из нулей, не найдено, то проводим минимальное число прямых через некоторые столбцы и строки так, чтобы все нули оказались вычеркнутыми. Выбираем наименьший невычеркнутый элемент. Этот элемент вычитаем из каждого невычеркнутого элемента и прибавляем к каждому элементу, стоящему на пересечении проведённых прямых.
Если после проведения 3-го шага оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.
Пример.
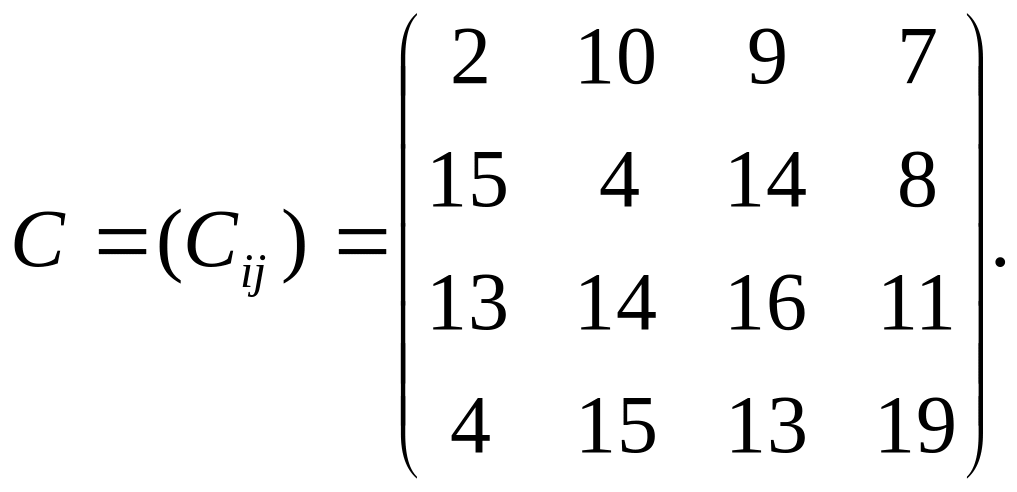
Распределить ресурсы по объектам.
РЕШЕНИЕ. 1-й шаг. Значения минимальных элементов строк 1, 2, 3 и 4 равны 2, 4, 11 и 4 соответственно. Вычитая из элементов каждой строки соответствующее минимальное значение, получим
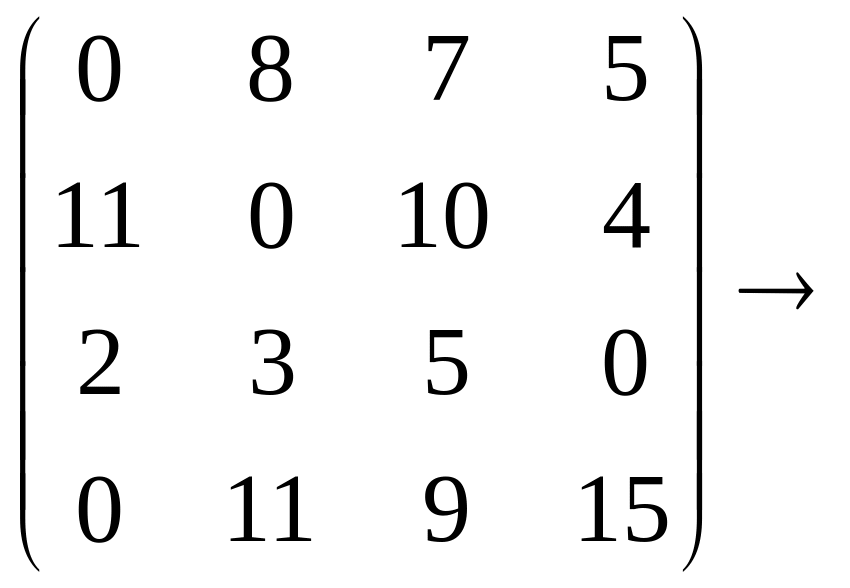
Значения минимальных элементов столбцов 1, 2, 3 и 4 равны 0, 0, 5, 0 соответственно. Вычитая из элементов каждого столбца соответствующее минимальное значение, получим
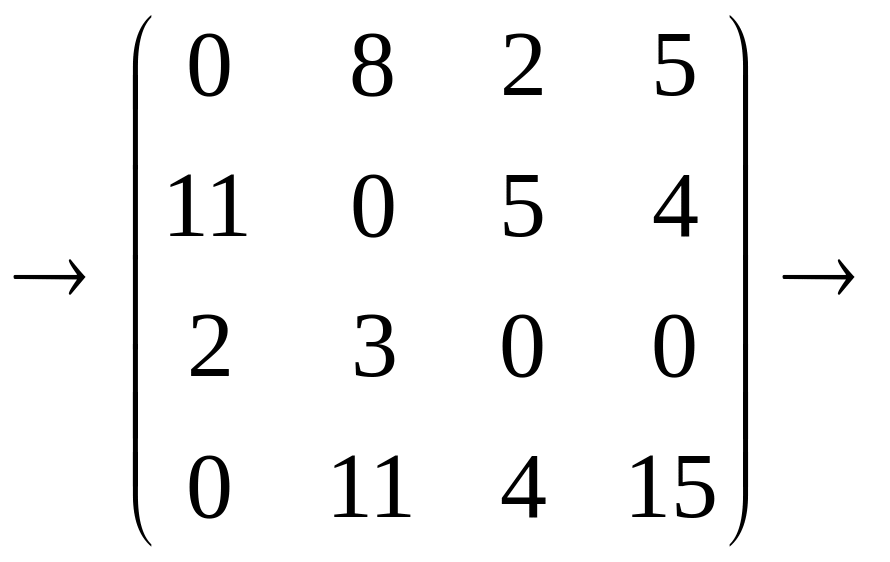
2-й шаг. Ни одно назначение не получено, необходимо провести модификацию матрицы стоимостей.
3-й шаг. Вычёркиваем столбец 1, строку 3, строку 2 (или столбец 2). Значение минимального невычеркнутого элемента равно 2:

 min
= 2.
min
= 2.
Вычитаем его из всех невычеркнутых элементов и, складывая его со всеми элементами, расположенными на пересечении двух линий, получим
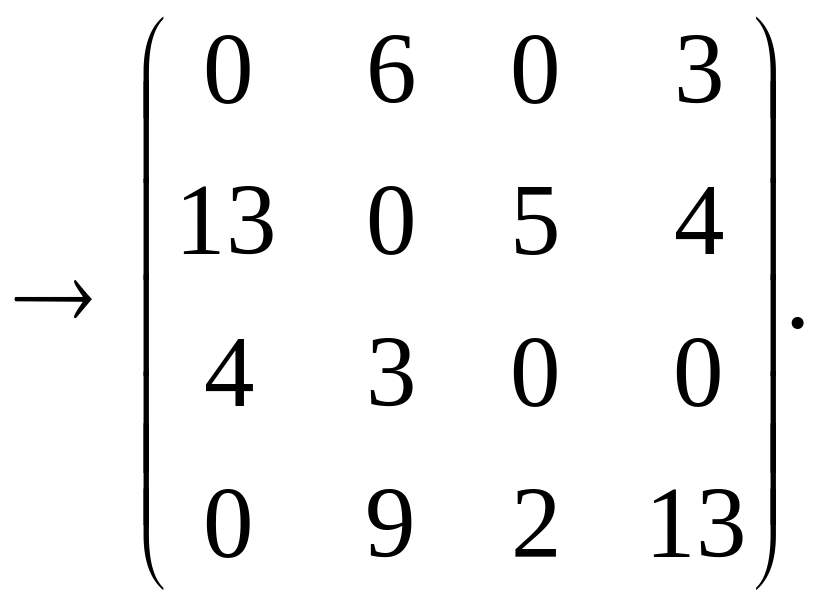 Итак,
Итак,
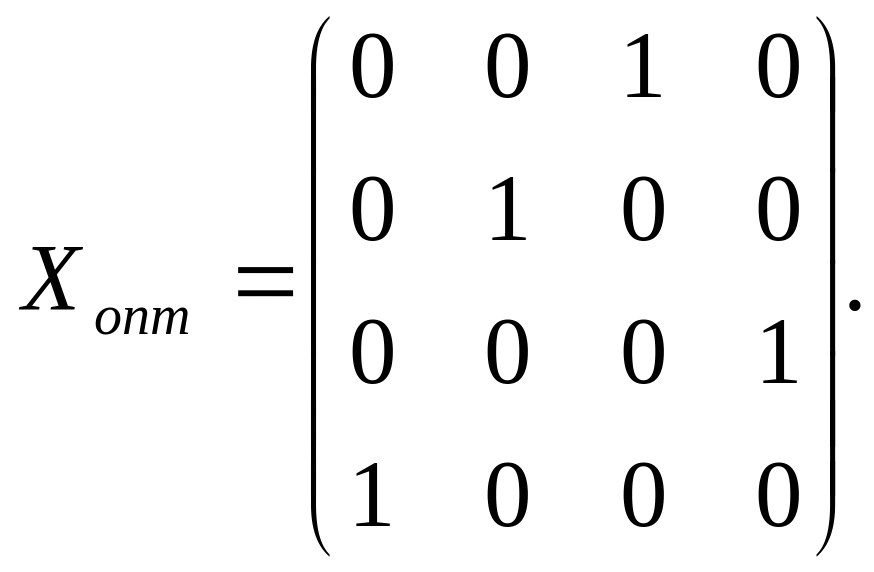
Ответ. Первый ресурс направляем на 3-й объект, второй – на 2-й объект, четвёртый – на 1-й объект, третий ресурс – на 4-й объект. Стоимость назначения: 9 + 4 + 11 + 4 = 28.
Примечания. 1. Если исходная матрица не является квадратной, то нужно ввести фиктивные ресурсы или фиктивные объекты, чтобы матрица стала квадратной.
2. Если какой-либо ресурс не может быть назначен на какой-то объект, то соответствующая стоимость полагается равной достаточно большому числу М.
3. Если исходная задача является задачей максимизации, то все элементы матрицы С следует умножить на (-1) и сложить их с достаточно большим числом так, чтобы матрица не сдержала отрицательных элементов. Затем задачу следует решать как задачу минимизации.
4. Если число линий, необходимое для того, чтобы вычеркнуть нулевые элементы, равно числу строк или столбцов (квадратной матрицы), то существует назначение нулевой стоимости.
Планирование загрузки оборудования
с учётом максимальной производительности
станков
На предприятии пять станков различных видов, каждый из которых может выполнять пять различных операций по обработке деталей. Известна производительность каждого станка при выполнении каждой операции, заданная матрицей
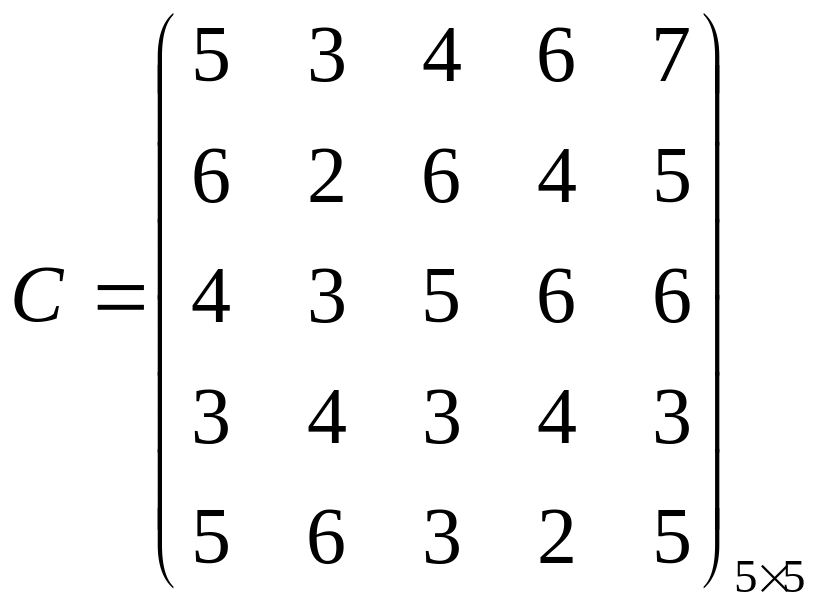 .
.
Определить, какую операцию и за каким станком следует закрепить, чтобы суммарная производительность была максимальной при условии, что за каждым станком закреплена только одна операция.
РЕШЕНИЕ. Так как в задаче требуется определить max, а алгоритм метода дан для задач на min, умножим матрицу С на (-1). Сложим полученную матрицу, имеющую отрицательные коэффициенты, с положительным числом, например, с числом 10. Получим
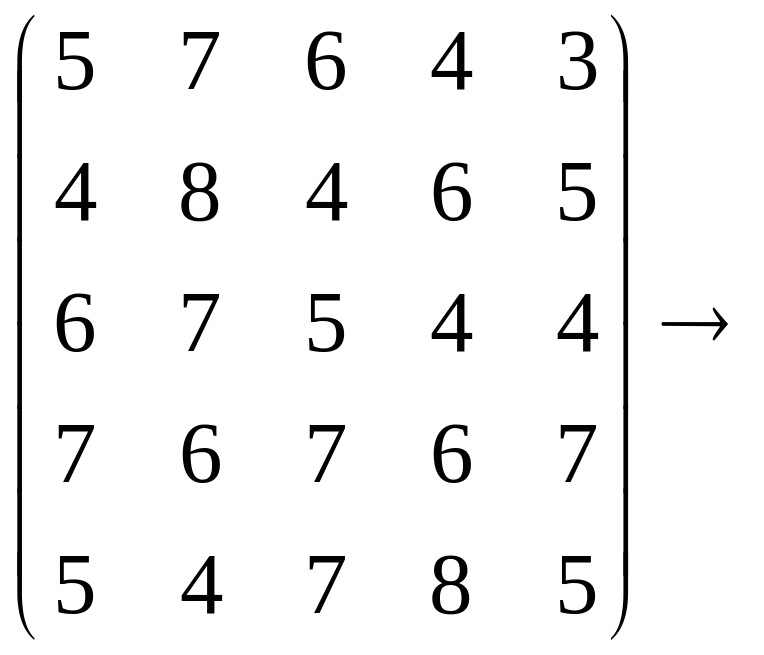
Минимальные элементы в строчках есть 3, 4, 4, 6, 4. Вычтем их из соответствующих элементов матрицы, получим
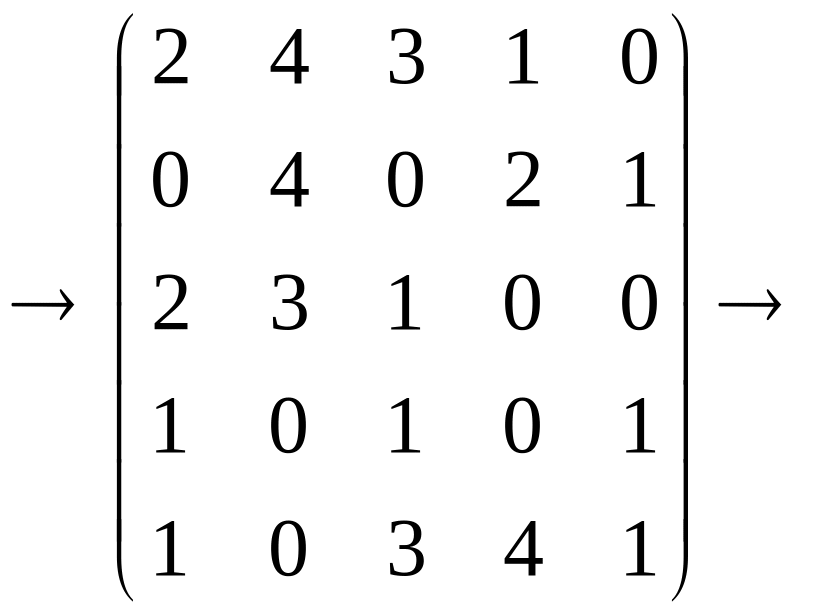
Т ак
как назначение не получено, вычёркиваем
строку 2, столбцы 2, 4, 5:
ак
как назначение не получено, вычёркиваем
строку 2, столбцы 2, 4, 5:

Минимальный элемент равен 1. Вычитаем его из всех невычеркнутых элементов и складываем со всеми элементами, расположенными на пересечении двух линий. Получаем
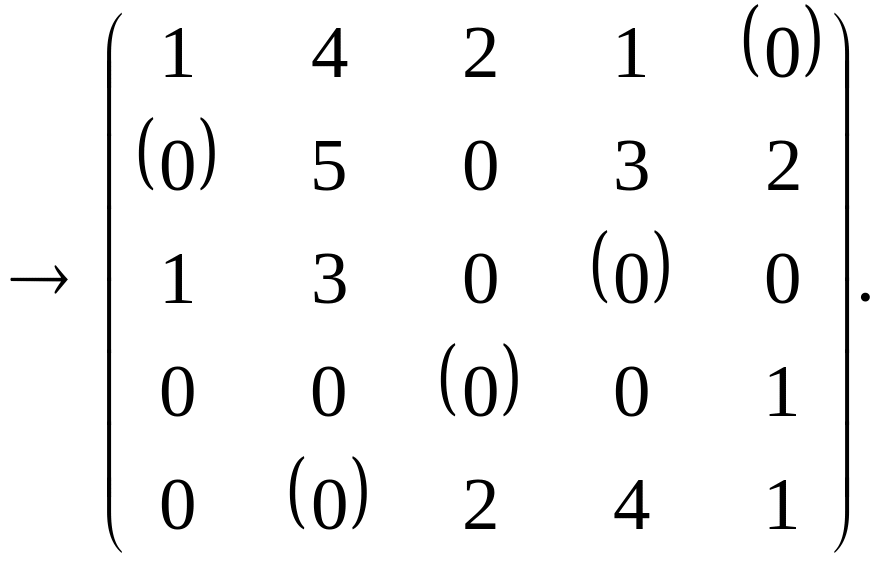
Оптимальное решение, соответствующее последней матрице, равно
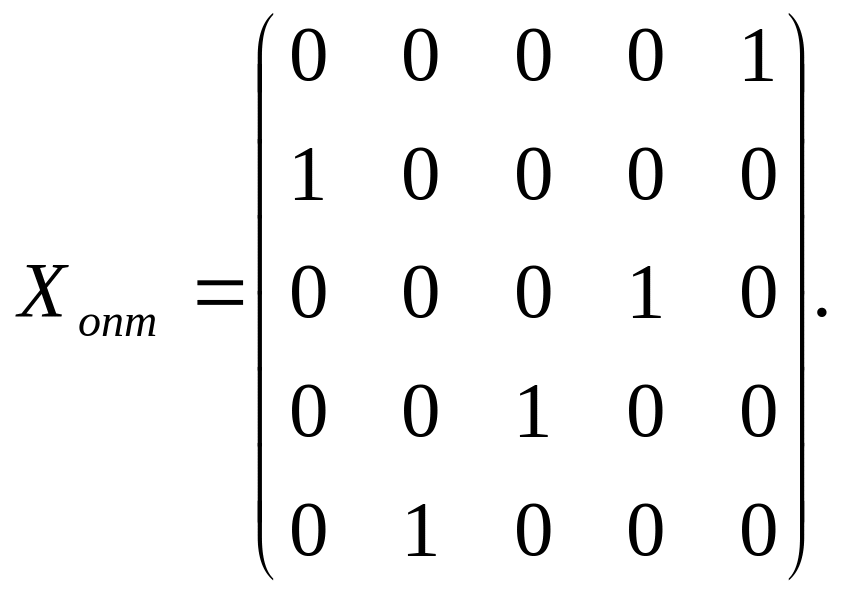
Суммарная производительность: 6 + 6 + 3 + 6 + 7 = 28.
Таким образом, на первом станке надо делать 5-ю операцию, на втором – 1-ю операцию, на третьем – 4-ю операцию, на четвёртом – 3-ю операцию, на пятом – 2-ю операцию. Суммарная производительность: 28 деталей в единицу времени.
