
- •Глава I элементы линейного программирования Лекция 1
- •1. Элементы аналитической геометрии
- •1.1. Основные понятия и определения
- •1.2. Решение систем т линейных уравнений с двумя переменными
- •Лекция 2
- •2. Графический метод
- •2.1. Постановка задачи
- •2.2. Алгоритм решения задач
- •2.3. Выбор оптимального варианта выпуска изделий
- •Лекция 3
- •3. Симплексный метод
- •3.1. Общая постановка задачи
- •3.2. Алгоритм симплексного метода
- •Лекция 3.
- •3.3. Анализ эффективности использования производственного потенциала предприятия
- •3.4. Альтернативный оптимум
- •Лекция 4
- •4. Двойственность в линейном программировании
- •4.1. Виды двойственных задач и составление их математических моделей
- •4.2. Основные теоремы двойственности
- •Исходная задача
- •Двойственная задача
- •Исходная задача
- •Двойственная задача
- •Лекция 6
- •5. Транспортная задача
- •5.1. Общая постановка задачи
- •5.2. Нахождение исходного опорного решения
- •5.3. Определение эффективного варианта доставки изделий к потребителю
- •5.4. Проверка найденного опорного решения на оптимальность
- •5.5. Переход от одного опорного решения к другому
- •5.6. Альтернативный оптимум в транспортных задачах
- •Вырожденность в транспортных задачах
- •Открытая транспортная задача
- •Определение оптимального варианта перевозки грузов
- •Приложение транспортных моделей к решению некоторых экономических задач.
- •Выбор оптимального варианта использования производственного оборудования
- •Лекция 10 Целочисленное программирование
- •Параметрическое программирование
- •1. Постановка задачи
- •2. Линейное программирование с параметром в целевой функции
- •Определение диапазона оптимального решения выпуска продукции при изменении условий реализации
- •Транспортная параметрическая задача
- •Лекция Задача о назначениях
- •Нелинейное программирование Общая постановка задачи
- •Графический метод
- •Дробно-линейное программирование
- •Алгоритм решения
- •Экономическая интерпретация задач дробно-линейного программирования
- •Применение дробно-линейного программирования для определения себестоимости изделий
- •Сведение экономико-математической модели дробно-линейного программирования к задаче линейного программирования
- •Метод множителей Лагранжа
- •Динамическое программирование
- •Оптимальная стратегия замены оборудования
- •Сетевые модели
- •Выбор оптимальной стратегии развития предприятия в условиях трансформации рынка
- •Принятие решения о замене оборудования в условиях неопределённости и риска
- •Элементы системы массового обслуживания (смо)
- •1. Формулировка задачи и характеристики смо
- •2. Смо с отказами
- •3. Смо с неограниченным ожиданием
- •4. Смо с ожиданием и с ограниченной длиной очереди
Транспортная параметрическая задача
Задача формулируется
следующим образом: для всех значений
параметра
,
где
![]() - произвольные действительные числа,
найти такие значения
- произвольные действительные числа,
найти такие значения
![]() ,
которые обращают в минимум функцию
,
которые обращают в минимум функцию
![]()
при ограничениях:
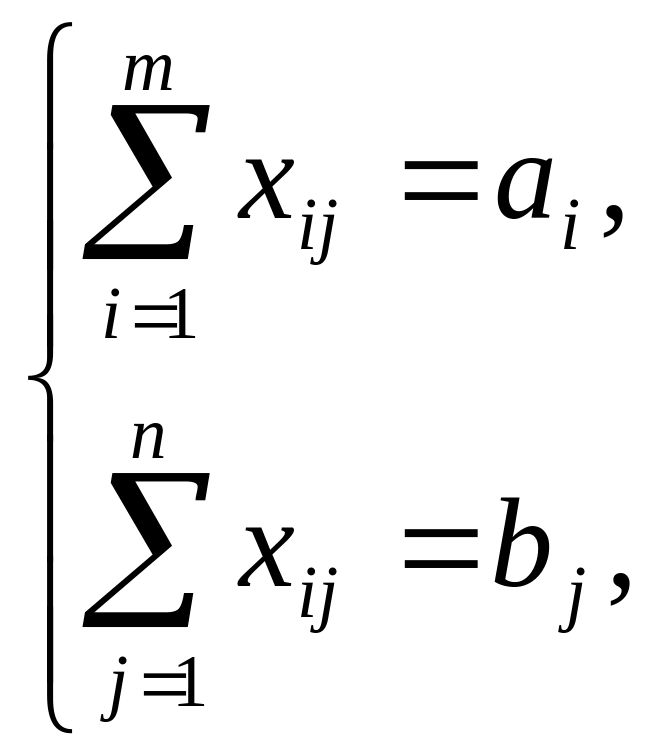
![]()
Пользуясь методом
потенциалов, решаем задачу при
![]() до получения оптимального решения.
Признаком оптимальности является
условие:
до получения оптимального решения.
Признаком оптимальности является
условие:
![]() для незанятых
клеток
для незанятых
клеток
и
![]() для занятых клеток,
для занятых клеток,
где
![]() - потенциалы строк, столбцов распределительной
таблицы.
- потенциалы строк, столбцов распределительной
таблицы.
Условие совместимости транспортной задачи записывается в виде
![]()
Значения
![]() и
и
![]() определяются из условия
определяются из условия
![]()
где
![]() определяются из систем уравнений
определяются из систем уравнений
![]()
Значения находятся в пределах :
![]()
![]()
Алгоритм решения.
Задачу решаем при конкретном значении параметра до получения оптимального решения.
Определяем и
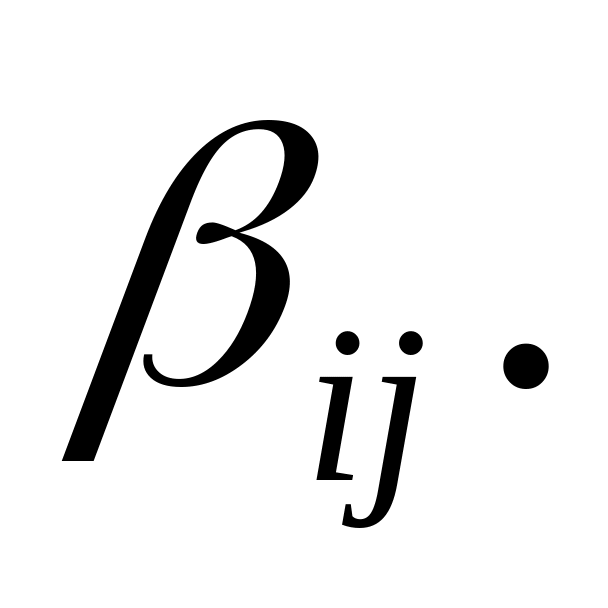
Вычисляем значения параметра .
Если
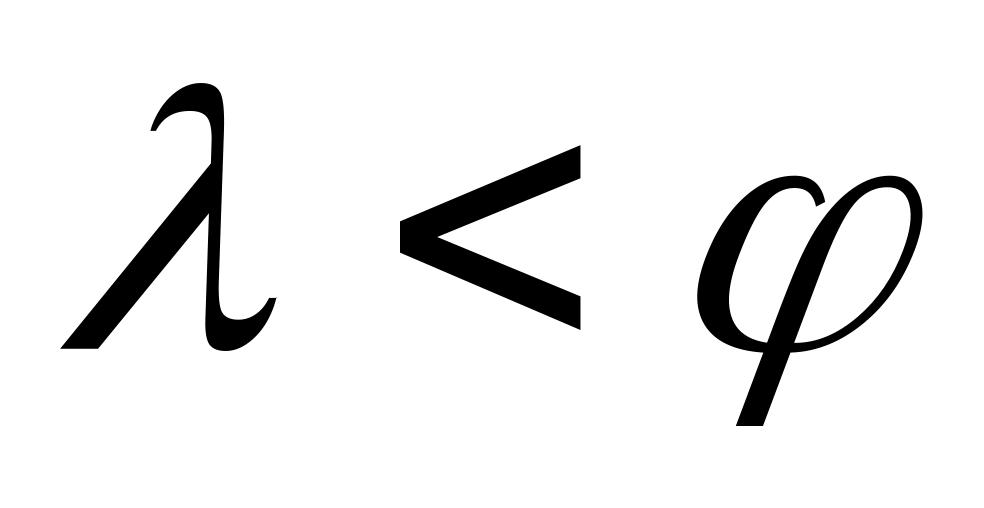 ,
производим перераспределение поставок
и получаем новое оптимальное решение.
Если
,
производим перераспределение поставок
и получаем новое оптимальное решение.
Если
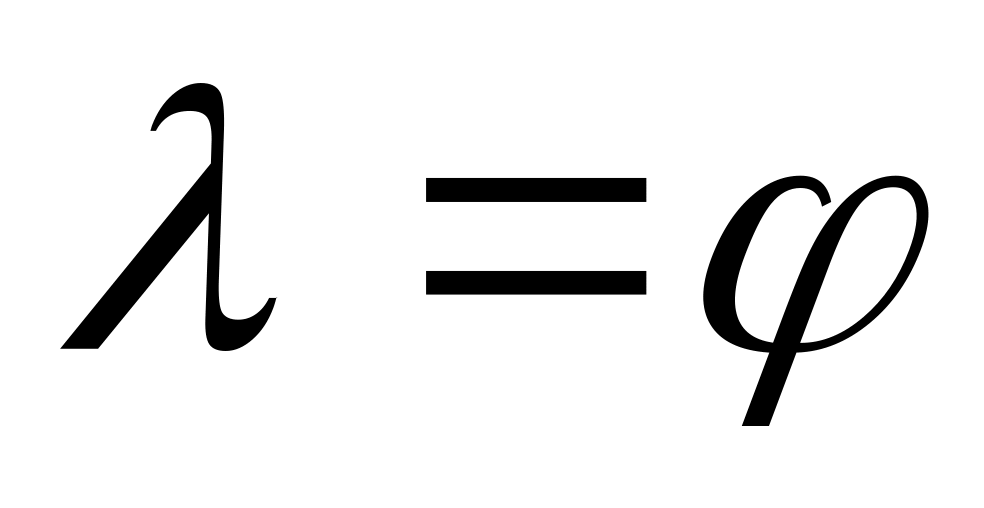 ,
то процесс решения окончен.
,
то процесс решения окончен.
Нахождение оптимальных путей транспортировки грузов при нестабильной загрузке дорог
Имеются три поставщика однородного товара с объёмами поставок: а1 = 100 т, а2 = 200 т, а3 = 100 т и четыре потребителя с объёмами потребления b1 = 80 т, b2 = 120 т, b3 = 150 т, b4 = 50 т. Стоимость транспортных расходов изменяется в определённом диапазоне в зависимости от загрузки дороги и задана матрицей
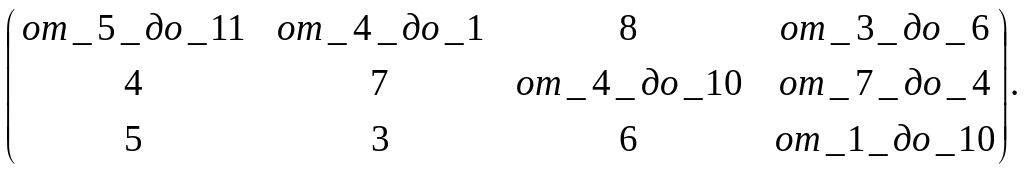
Определить оптимальное решение перевозок, обеспечивающее минимальные транспортные затраты.
РЕШЕНИЕ. В матрицу
расходов введём параметр
,
где
![]() .
Получим
.
Получим
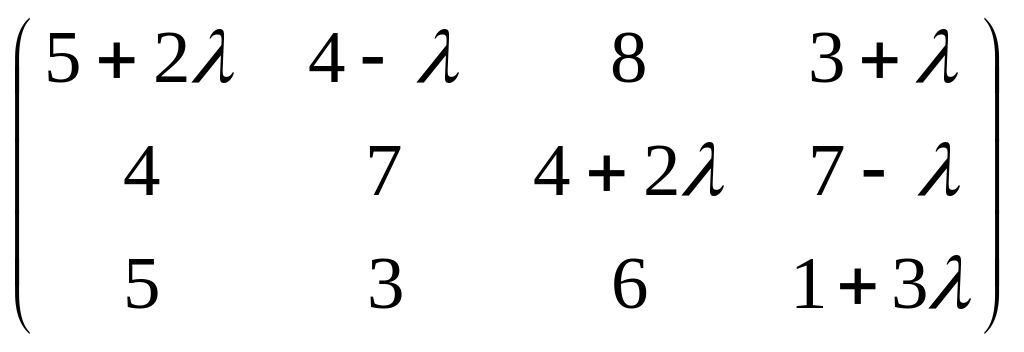 .
.
Полагая , решаем задачу методом потенциалов, определим оптимальное решение перевозок. Распределительная таблица этого решения будет иметь вид:
bj ai |
80 |
120 |
150 |
50 |
ui |
100 |
30 |
4- 70 |
8 |
|
0 |
200 |
4 50 |
7 |
150 |
|
|
100 |
5 |
3 50 |
6 |
50 |
|
vj |
|
|
|
|
|
В таблице ui и vj – потенциалы строк и столбцов. Для занятых клеток они определяются из условия
![]()
Полагая u1
= 0,
![]() ,
получаем
,
получаем
![]()
![]() ,
откуда
,
откуда
![]()
![]() или
или
![]() откуда
откуда
![]()
![]() или
или
![]()
![]()
Аналогично находим,
что
![]()
Оценки свободных клеток находим по формуле
![]()
Имеем
![]()
![]()
![]()
Аналогично находим,
что
![]()
![]()
![]()
Решение, полученное при , является оптимальным для всех значений параметра , удовлетворяющих условию
![]() или
или
Имеем
![]()
![]()
![]()
Так как по условию
задачи
![]() ,
то оптимальное решение сохраняется при
,
то оптимальное решение сохраняется при
![]() При этом минимальная стоимость
транспортных расходов составляет
При этом минимальная стоимость
транспортных расходов составляет
![]()
Таким образом, при
![]()
![]() и
и
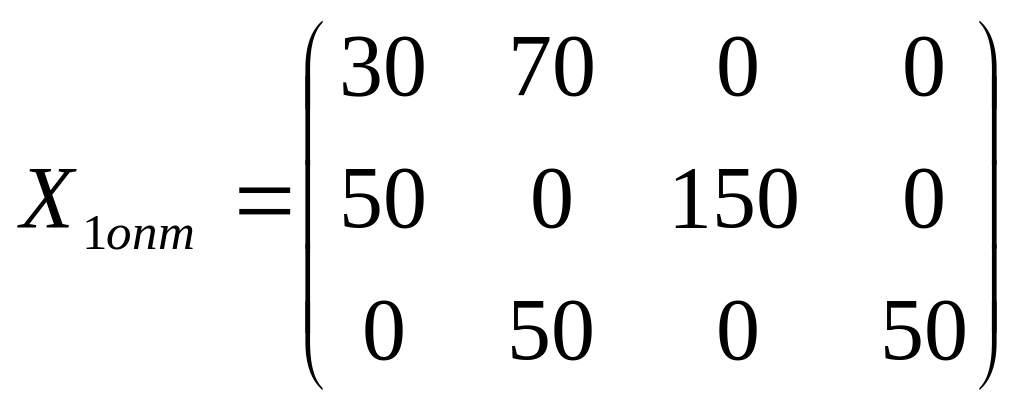 .
.
Чтобы получить
оптимальное решение при
![]() ,
перераспределим поставки товаров в
клетку (3, 1), где
,
перераспределим поставки товаров в
клетку (3, 1), где
![]() .
Вновь полученное распределение
представлено в табл.:
.
Вновь полученное распределение
представлено в табл.:
bj ai |
80 |
120 |
150 |
50 |
ui |
100 |
|
4- 100 |
8 |
|
0 |
200 |
4 50 |
7 |
150 |
|
|
100 |
5 30 |
3 20 |
6 |
50 |
|
vj |
|
|
|
|
|
Находим оценки свободных клеток:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Определим пределы изменения :
![]()
![]()
Полученное в
таблице оптимальное решение сохраняется
при
![]() При этом
При этом
![]() .
.
Итак,
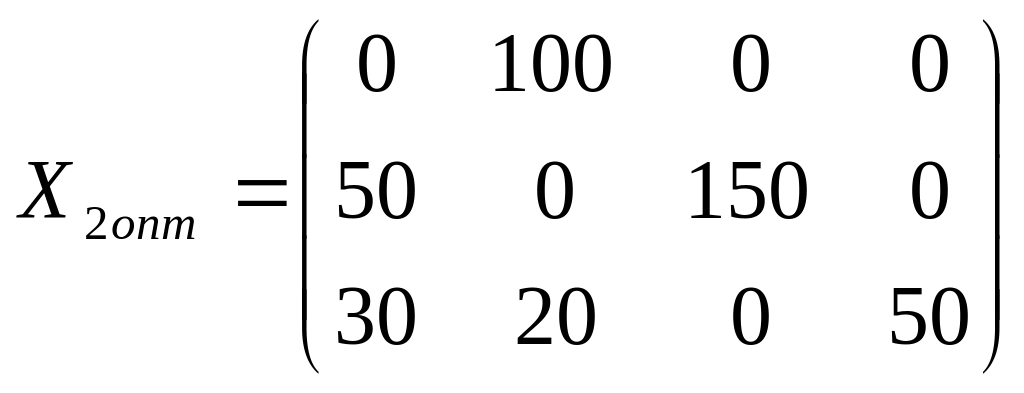 .
.
Перераспределим
поставки грузов в клетку (3, 3), где
![]() .
Получим новое распределение:
.
Получим новое распределение:
bj ai |
80 |
120 |
150 |
50 |
ui |
100 |
|
4- 100 |
8 |
|
0 |
200 |
4 80 |
7 |
120 |
|
|
100 |
5
|
3 20 |
6 30 |
50 |
|
vj |
|
|
|
|
|
Находим оценки свободных клеток:
![]()
![]()
![]()
![]()
![]() .
.
Определим пределы изменения :
![]()
![]()
Оптимальное решение
сохраняется при
![]() При этом
При этом
![]() .
.
Итак,
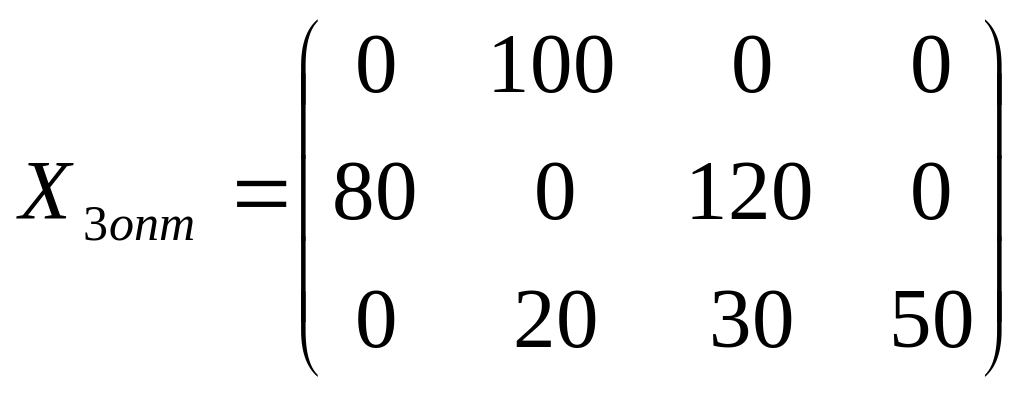 .
.
Перераспределим
поставки грузов в клетку (1, 4), где
![]() .
.
bj ai |
80 |
120 |
150 |
50 |
ui |
100 |
|
4- 50 |
8 |
50 |
0 |
200 |
4 80 |
7 |
120 |
|
|
100 |
5
|
3 70 |
6 30 |
|
|
vj |
|
|
|
|
|
Оценки свободных клеток:
![]()
![]()
![]()
![]() .
.
Пределы изменения :
![]()
![]()
Полученное в
предыдущей таблице оптимальное решение
сохраняется при
![]() При этом
При этом
![]() .
.
Итак,
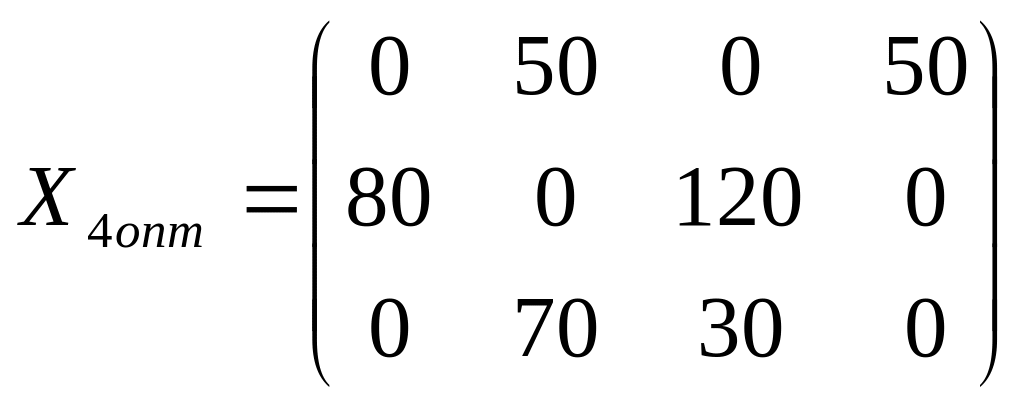 .
.
Перераспределим
поставки грузов в клетку (2, 4), где
![]() .
.
bj ai |
80 |
120 |
150 |
50 |
ui |
100 |
|
4- 100 |
8 |
|
0 |
200 |
4 80 |
7 |
70 |
50 |
|
100 |
5
|
3 20 |
6 80 |
|
|
vj |
|
|
|
|
|
Оценки свободных клеток:
![]()
![]() .
.
Пределы изменения :
![]()
![]()
Оптимальное решение
сохраняется при
![]() При этом
При этом
![]() .
.
Итак,
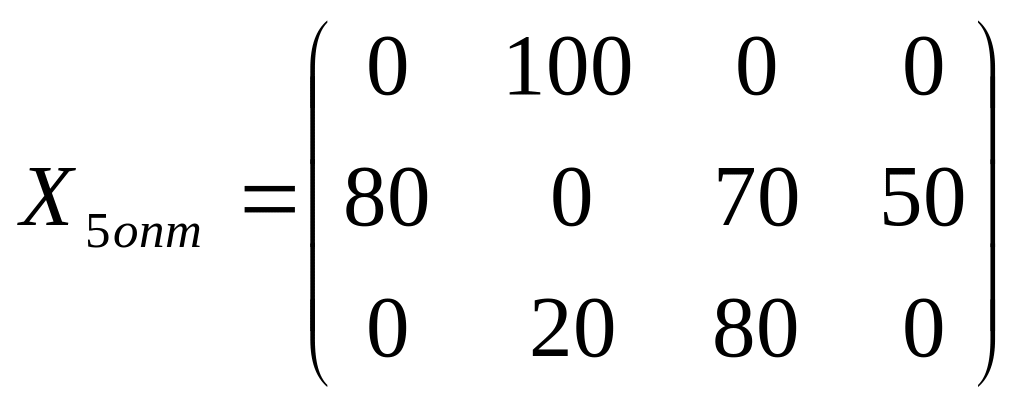 .
.
