
- •2. Определение матриц. Виды матриц.
- •1. Математическая модель. Этапы математического моделирования.
- •3. Транспонирование матриц. Свойства.
- •5. Произведение матриц. Возведение матриц в степень. Свойства произведения.
- •6. Вычисление определителей 2-го и 3-го порядков. Свойства определителей.
- •7. Минор и их алгебраическое дополнение элемента матрицы.
- •8. Вычисление определителей n-го порядка разложением по ряду и приведением к треугольному виду.
- •9. Определение обратной матрицы. Условие существования обратной матрицы. Формула нахождения обратной матрицы.
- •11. (Только практика) Способы вычисления ранга.
- •12.Сформулировать элементарные преобразования матриц. Определение эквивалентных матриц.
- •15.(Только практика) Решение системы матричным способом.
- •16.(Только практика) Решение системы методом Крамера.
- •17.(Только практика) Решение системы методом Гаусса.
- •18.Совместная и несовместная система. Критерий совместности системы. Правила практического разыскания решений.
- •19.(Только практика) Алгоритм решения произвольной системы линейных уравнений.
- •20.Определение однородной системы уравнений. Сформулировать теорему об условии существования нетривиального решения. Что называется фундаментальной системой решения?
- •21.Определение вектора, противоположного вектора, длины вектора, нулевого и единичного векторов, коллинеарных. Равных и компланарных векторов.
- •22.Линейные операции над векторами.
- •23.Формула разложения вектора по ортам координатных осей. Координаты вектора. Выражение линейных операций над векторами в координатах.
- •24.Формула деления отрезка в заданном отношении.
- •25.Определение скалярного произведения векторов. Выражение скалярного произведения через координаты.
- •26. Как найти угол между векторами?
- •27.Определение n-мерного вектора и его координат. Определение векторного пространства. Как найти сумму, произведение на число, скалярное произведение и длину n-мерных векторов?
- •28.Линейная комбинация векторов. Определение линейно зависимой и независимой системы.
- •29.Уравнения прямой на плоскости (6 видов).
- •30.Угол между прямыми и условия параллельности и перпендикулярности двух прямых.
- •31.Расстояние от точки до прямой.
- •32.Уравнения плоскости в пространстве (4 вида).
- •33.Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
- •34.Расстояние от точки до плоскости.
- •35.Уравнения прямой в пространстве (4 вида)
- •40.Определение гиперболы и се каноническое уравнение. Исследование формы гиперболы. Асимптоты гиперболы. Дополнительные сведения о гиперболе.
- •41.Парабола и ее каноническое уравнение. Исследование формы параболы.
- •43.Определение предела последовательности и его геометрическая интерпретация.
- •44.Свойства сходящихся последовательностей.
- •45.Определение, способы задания и свойства функции.
- •46.1)Определение предела функции в точке 2)Предел функции при х→∞ 3)Односторонние пределы.
- •47.Бесконечно малые и бесконечно большие функции и их свойства.
- •48.Основные свойства пределов.
- •49.Замечательные пределы (1-й - с доказательством).
- •50.Определение функции непрерывной в точке, в интервале и на отроке. Точки разрыва.
- •51.Определение производной функции в точке. (производная – это скорость).
- •52. Механический, геометрический и экономический смысл производной.
- •53.Таблица производных элементарных функций. Правила вычисления производных.
- •54.Дифференциал функции и его геометрическая интерпретация. Свойства дифференциала.
- •55.Производные и дифференциалы высших порядков.
30.Угол между прямыми и условия параллельности и перпендикулярности двух прямых.
Угол
между прямыми. Пусть 2 прямые заданы
уравнениями
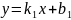 и
и
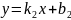 .
По теореме о внешнем угле треугольника
.
По теореме о внешнем угле треугольника
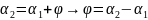 .
.
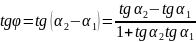 .
.
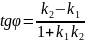 .
.
Если
прямые заданы уравнениями
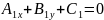 и
и
 ,
то
,
то
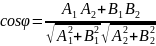 .
.
Если
прямая а параллельна b,
то угол между ними считается
 ,
,
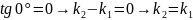 – условие параллельности прямых. A
перпендикулярна b,
тогда угол =90,
– условие параллельности прямых. A
перпендикулярна b,
тогда угол =90,
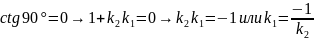 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
31.Расстояние от точки до прямой.
Требуется
найти расстояние от точки
 .
.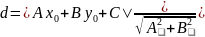
32.Уравнения плоскости в пространстве (4 вида).
1.
Уравнение плоскости, проходящей через
данную точку перпендикулярно данному
вектору. Пусть плоскость задана точкой
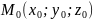 и вектором
и вектором
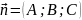 ,
перпендикулярным плоскости. Рассмотрим
производную точку
,
перпендикулярным плоскости. Рассмотрим
производную точку
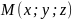 .
.
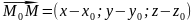 .
перпендикулярно
.
перпендикулярно
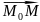 следовательно
следовательно
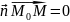 .
.
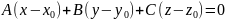
2.
Общее
уравнение плоскости. Имеет вид:
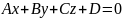 .
Докажем, что это уравнение плоскости:
Пусть
,
тогда
.
Докажем, что это уравнение плоскости:
Пусть
,
тогда
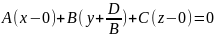 – получим уравнение вида 1, а значит,
данное уравнение является уравнением
плоскости.
– получим уравнение вида 1, а значит,
данное уравнение является уравнением
плоскости.
Частные
случаи: 1.
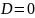 – проходит через начало координат. 2.
– проходит через начало координат. 2.
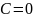 - ||
;
- ||
;
 - ||
;
- ||
;
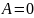 - ||
.
3.
- ||
.
3.
 – проходит через
;
… 4.
– проходит через
;
… 4.
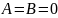 ||
||
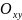 ,
… 5.
,
… 5.
 -
,
… .
-
,
… .
3.
. Уравнение плоскости проходящей через
3 точки. Пусть плоскость проходит через
точки
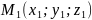 ,
,
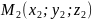 и
и
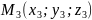 .
.
4.
Уравнение плоскости в отрезках. Пусть
плоскость пересекает оси в точках
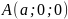 ,
,
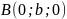 и
и
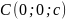 .
Подставим в уравнение 3 координаты
точек. Преобразуем определитель,
получим:
.
Подставим в уравнение 3 координаты
точек. Преобразуем определитель,
получим:
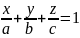 .
.
33.Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
Угол
между двумя плоскостями.
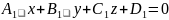 ,
,
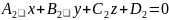 ,
,
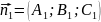 ,
,
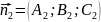 ,
,
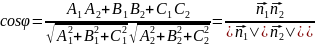 .
.
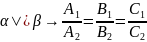 – условие
параллельности плоскостей;
– условие
параллельности плоскостей;
 - условие перпендикулярности плоскостей.
- условие перпендикулярности плоскостей.
34.Расстояние от точки до плоскости.
Требуется
найти расстояние от точки
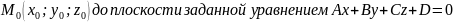 .
.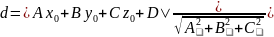
35.Уравнения прямой в пространстве (4 вида)
1.
Общее уравнение прямой. Прямую в
пространстве можно задать как пересечение
2ух плоскостей.
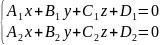
2.
Каноническое уравнение прямой. Прямую
в пространстве можно задать точкой
и вектором
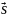 ,
параллельным этой прямой, который
называется направляющим. Пусть
,
параллельным этой прямой, который
называется направляющим. Пусть
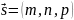 .
.
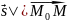 ,
,
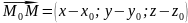 ,
,
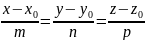
3.
Параметрическое уравнение прямой.
Обозначим в каноническом уравнении:
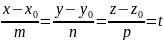 – параметр.
– параметр.
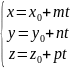
4.
Уравнение прямой, проходящей через 2
точки. Пусть
прямая задана точками
и
.
 ,
следовательно
,
следовательно
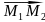 можно считать направляющим вектором.
Тогда согласно каноническому уравнению:
можно считать направляющим вектором.
Тогда согласно каноническому уравнению:
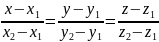
36.Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых в пространстве.
Угол
между прямыми в пространстве. Под углом
между прямыми в пространстве понимают
угол между направляющими векторами
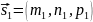 и
и
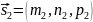 .
.
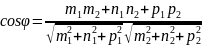 .
.
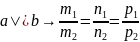 – условие
параллельности прямых;
– условие
параллельности прямых;
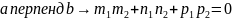 - условие перпендикулярности прямых.
- условие перпендикулярности прямых.
37.Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
– направляющий
вектор L.
– вектор перпенд L.
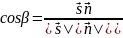 .
.
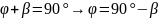 ,
,
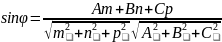
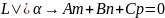 –
условие
параллельности прямой и плоскости;
–
условие
параллельности прямой и плоскости;
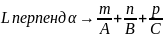 - условие перпендикулярности прямой и
плоскости.
- условие перпендикулярности прямой и
плоскости.
38.Условие принадлежности прямой плоскости.
Учитывая
условие параллельности прямой и
плоскости и то, что любая точка прямой
принадлежит плоскости, если прямая
лежит в плоскости, получим условие
принадлежности прямой и плоскости.
 .
.
39.Определение эллипса и его каноническое уравнение. Исследование формы эллипса. Дополнительные сведения об эллипсе.
Рассмотрим линии, определяемые уравнениями второй степени относительно текущей координаты. Такие линии называются кривыми второго порядка. Примером такой кривой является окружность.
Эллипсом
называют множество всех точек плоскости,
сумма расстояний от каждой из которых
до 2ух данных точек этой плоскости,
называемых фокусами, есть величины
постоянная, большая, чем расстояние
между фокусами.
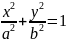 – каноническое уравнение эллипса, где
– каноническое уравнение эллипса, где
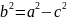 .
.
Исследование формы эллипса:
1.
Уравнение эллипса содержит x
и y
только в четных степенях, поэтому если
эллипсу принадлежат точки
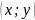 ,
то ему будут принадлежать точки
,
то ему будут принадлежать точки
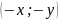 ,
,
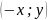 ,
,
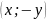 – эллипс симметричен относительно
,
и начала координат. Точка
– эллипс симметричен относительно
,
и начала координат. Точка
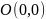 – центр эллипса.
– центр эллипса.
2.
Точки пересечения с осью
:
y=0,
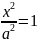 ,
,
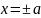 .
.
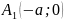 и
и
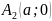 – вершины эллипса. С
осью
:
x=0,
– вершины эллипса. С
осью
:
x=0,
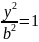 ,
,
 .
.
 и
и
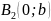 .
Отрезки
.
Отрезки
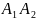 и
и
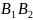 называют большой и малой осями эллипса.
называют большой и малой осями эллипса.
3.
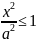 и
и
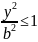 .
.
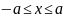 и
и
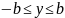 .
Все точки эллипса расположены внутри
прямоугольника, образованного прямыми
и
.
.
Все точки эллипса расположены внутри
прямоугольника, образованного прямыми
и
.
Из
уравнения эллипса следует, что
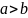 .
Если же
.
Если же
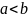 ,
то уравнение эллипса определяет, что
эллипс будет вытянут вдоль оси
и на оси
будут находиться фокусы.
,
то уравнение эллипса определяет, что
эллипс будет вытянут вдоль оси
и на оси
будут находиться фокусы.
