5. Произведение матриц. Возведение матриц в степень. Свойства произведения.

Операция умножения двух матриц вводится только для случая, когда число столбцов 1-ой матрица равно числу строк 2-ой матрицы. Такие матрицы называются согласованными.

Произведением двух согласованных матриц называется матрица, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующий элемент j-ого столбца матрицы В.

Матрицу можно умножать саму на себя, тоесть возводить в целую положительную степень, тогда и только тогда, когда она квадратная.

Свойства степени:

1.

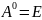
2.

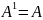
3.

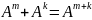
4.

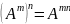
Свойства произведения матриц:

1. А(ВС)=(АВ)С

2. (А+В)С=АС+ВС

3. С(А+В)=СА+СВ

4. α(АВ)=(αА)В=А(αВ)

6. Вычисление определителей 2-го и 3-го порядков. Свойства определителей.

Квадратной матрице А порядка m можно поставить в соответствие число, называемое ее определителем. Обозначается: detA; ∆A;|A|. Вычисляются:

N=2: ,

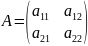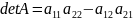
N=3: ,

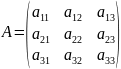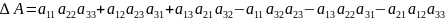
Правило треугольника и правило диагоналей.

Свойства определителей:

1. Если какой-либо ряд состоит из одних нулей, то его определитель равен 0.

2. Определитель не изменяется при транспонировании матрицы.

3. При перестановке 2ух строк (столбцов) в матрице, ее определитель меняет знак.

4. Определитель, имеющий 2 одинаковых ряда равен 0.

5. Общий множитель любого ряда можно выносить за знак определителя.

6. Если элементы 2ух строк (столбцов) определителя пропорциональны, то определитель равен 0.

7. Если каждый элемент строки/столбца представлен в виде суммы 2ух слагаемых, то этот определитель равен сумме 2ух определителей.

8. Определитель не меняется, если к элементам любой строки/столбца прибавить соответствующие элементы другой строки/столбца, умноженные на любое число.

9. Определитель произведения 2ух квадратных матриц равен произведению их определителей.

10. Теорема Оннулирования. Сумма произведений произвольных элементов одной из строк/столбцов матрицы на алгебраическое дополнение соответствующих элементов другой строки/столбца равна нулю.

11. Теорема замещения. Сумма произведений произвольных n-чисел 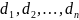на алгебраическое дополнение элементов некоторой строки/столбца матрицы порядка n равна определителю матрицы, который получается из данной заменой элементов указанной строки/столбца на числа .

7. Минор и их алгебраическое дополнение элемента матрицы.

Минором 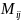элемента матрицы n-ого порядка называется определитель (n-1) – ого порядка, полученный путем вычеркивания из определителя n-ого порядка i-ой строки и j-ого столбца на пересечении которых находится выбранный элемент.

Алгебраическим дополнением элемента матрицы n-ого порядка называется его минор, взятый со знаком «+», если сумма i+j – четное число, и со знаком «-», если сумма i+j – нечетное число. Обозначается

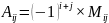
8. Вычисление определителей n-го порядка разложением по ряду и приведением к треугольному виду.

Определитель равен сумме произведений элементов любой строки/столбца на их алгебраическое дополнение.

Формула разложения определителя по строке (аналогично по столбцу). Удобнее делать в рядах с максимальным количеством нулей. Также рекомендуется обнулить ряд, то есть преобразовать определитель так, чтобы в столбце/строке получились все нулевые элементы кроме одного.

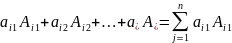
2 способ – Приведение определителя к треугольному виду. Определитель приводиться к треугольному виду, а в конце перемножаются элементы его диагонали.