15.(Только практика) Решение системы матричным способом.

Метод обратной матрицы.

Применим только для случая, когда число уравнений равно числу неизвестных.

Основная матрица системы – квадратная порядка n. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то матрица А – невырожденная и существует обратная матрица .

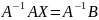
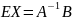
, то есть решение системы существует.

Если определитель системы = 0, то система не имеет решения.

16.(Только практика) Решение системы методом Крамера.

Применим только для случая, когда число уравнений равно числу неизвестных.

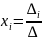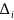, где ∆ - определитель основной матрицы; – определитель, полученный из определителя ∆ заменой i-ого столбца столбцом свободных членов матрицы b.

17.(Только практика) Решение системы методом Гаусса.

Применим для решения систем общего вида, содержащих m уравнений и n неизвестных.

Метод Гаусса – метод последовательного исключения переменных. Заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе трапециевидного или треугольного вида (прямой ход), из которого последовательно, начиная с последних по номеру переменных находятся все остальные переменные (обратный ход).

Прямой ход.

1. Составить расширенную матрицу системы. (Расширенная матрица системы получается из основной матрицы приписыванием столбца свободных членов).

2. С помощью элементарных преобразований строк расширенной матрицы приводим ее к трапециевидному или треугольному виду.

3. Если число ненулевых строк преобразованной матрицы равно числу ненулевых строк части матрицы, стоящей слева от вертикальной черты, то система совместна. В противном случае она несовместна.

Обратный ход.

1. Если преобразованная матрица приведена к треугольному виду, то система имеет единственное решение, начиная с последнего ее уравнения последовательно находят значения всех ее неизвестных.

2. Если преобразованная система имеет трапециевидный вид, то система имеет бесконечное множество решений. В этом случае неизвестные называют свободными и формируют правые части уравнений, оставим в левых частях слагаемые, содержащие базисные переменные. Количество базисных переменных равно количеству ненулевых строк трапециевидной матрицы (равно рангу матрицы).

18.Совместная и несовместная система. Критерий совместности системы. Правила практического разыскания решений.

Система уравнений называется совместной, если она имеет хотя бы одно решение и не совместной, если она не имеет решений.

Теорема, критерий совместности системы. Система линейных уравнений совместна тогда и только тогда, когда ранг ее расширенной матрицы равен рангу ее основной матрицы.

Правила практического разыскания решений системы:

1. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

2. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.