
- •Натуральные числа
- •Метод математической индукции.
- •Бином Ньютона, треугольник Паскаля
- •Целые числа
- •Рациональные числа
- •Числовые кольца, поля
- •Вещественные числа
- •Поле комплексных чисел
- •Комплексная плоскость.
- •Извлечение корней, корни из единицы
- •Делимость многочленов. Наибольший общий делитель. Алгоритм Евклида. Расширенный алгоритм Евклида.
- •Разложение рациональных функций в сумму дробей.
- •Неприводимый многочлен, его свойства
- •Из вытекает, либо , либо .
- •Если неприводимый многочлен делится на неприводимый многочлен, то они отличаются числовым множителем.
- •Корень многочлена.
- •Интерполяционный многочлен
- •Интерполяционный многочлен в форме Лагранжа
- •Интерполяционный многочлен в форме Ньютона
- •Разложение многочлена над полем рациональных чисел
- •Примитивный многочлен, его свойства
- •Критерий Эйзенштейна
- •Все коэффициенты многочлена f(X), кроме старшего, делятся на p
- •Старший коэффициент не делится на p
- •Свободный член не делится на
- •Метод Кронекера разложения многочлена на неприводимые многочлены над кольцом целых чисел.
- •Рациональные корни.
- •Присоединение корня. Поле разложения многочлена.
- •Формальная производная, ее свойства
- •Производные высоких порядков
- •Интерполяционный многочлен Лагранжа-Сильвестра
- •Формулы Виета
- •Симметрические полиномы
- •Формулы Кардано
- •Способ Феррари
- •Дискриминант
- •Основная теорема Алгебры
- •Разложение многочлена на неприводимые множители над полем вещественных чисел
- •Теорема Штурма
- •Любые два соседних многочлена не имеют общих корней
- •Последний многочлен не имеет вещественных корней.
- •Если в окрестностях корня a многочлена сам многочлен возрастает, то , а если убывает, то
- •Метод Гаусса решения системы линейных уравнений
- •Равносильные преобразования
- •Умножение строки не ненулевое число.
- •Перестановка строк
- •Прибавление к некоторой строке другой строки, умноженной на число.
- •Метод Гаусса.
- •Перестановки
- •Четность перестановок
- •Определитель
- •Свойства определителя
- •Изменит знак при перестановке столбцов
- •Равен нулю, если имеется два одинаковых столбца
- •Не изменится при прибавлении к столбцу другого столбца, умноженного на число.
- •Вычисление определителей произвольных порядков
- •Определитель Вандермонда
- •Теорема Лапласа
- •Умножение матриц
- •Формула Бине-Кощи
- •Операции с матрицами
- •Обратная матрица
- •Правило Крамера
- •Матрица элементарных преобразований
- •Построение обратной матрицы
- •Блочные матрицы
- •Алгоритм Штрассена
- •Кронекерово произведение
- •Формула Фробениуса
- •Линейные пространства.
- •. Линейная зависимость. Теорема о замене. Ранг системы.
- •Конечномерные пространства. Базис. Размерность. Дополнение до базиса. Базис суммы, пересечения.
- •. Прямая сумма подпространств. Проекция.
- •Изменение координат вектора при изменении базиса.
- •Изоморфизм линейных пространств.
- •Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.
- •Ранги матрицы.
- •Общее решение системы линейных уравнений.
- •Двойственное пространство
- •Взаимное расположение линейных многообразий в пространстве.
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Симметричность .
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
-
Взаимное расположение линейных многообразий в пространстве.
С помощью рангов соответствующих матриц можно определить взаимное расположение подпространств из некоторого пространства. При этом определённую пользу принесёт следующая теорема.
Теорема 7.49 Кронекера-Капели.
Система
![]() совместна тогда и только тогда, когда
совместна тогда и только тогда, когда
![]() .
.
Доказательство. Очевидно.
В качестве примера определим взаимное
расположение двух линейных многообразий:
![]()
![]() и
и
![]()
![]() (предполагается линейная независимость
систем векторов
(предполагается линейная независимость
систем векторов
![]() и
и
![]() ).
Рассмотрим две системы линейных уравнений
).
Рассмотрим две системы линейных уравнений
![]() и
и
![]() .
Положим
.
Положим
![]() и
и
![]() .
.
Совместность первой системы означает,
что у линейных многообразий есть общая
точка. Равенство рангов
![]() является необходимым и достаточным
условием совместности первой системы
линейных уравнений (теорема
Кронекера-Капели). Размерность пространства
решений второй системы позволяет
определить размерность пересечения
линейных оболочек
является необходимым и достаточным
условием совместности первой системы
линейных уравнений (теорема
Кронекера-Капели). Размерность пространства
решений второй системы позволяет
определить размерность пересечения
линейных оболочек
![]() и
и
![]() по формуле
по формуле
![]() .
Этой информации достаточно для описания
взаимного расположения линейных
многообразий. В качестве примера приведём
в таблицах все случаи взаимного
расположения двух прямых, прямой и
плоскости, двух плоскостей.
.
Этой информации достаточно для описания
взаимного расположения линейных
многообразий. В качестве примера приведём
в таблицах все случаи взаимного
расположения двух прямых, прямой и
плоскости, двух плоскостей.
Две прямые (k=s=1)
|
r |
R |
примечание |
|
1 |
1 |
Прямые совпадают (есть общая точка и размерность пересечения равна 1) |
|
1 |
2 |
Прямые параллельны |
|
2 |
2 |
Прямые пересекаются в одной точке |
|
2 |
3 |
Прямые скрещиваются (нет общих точек и не параллельны) |
Прямая и плоскость (k=1, s=2)
|
r |
R |
примечание |
|
2 |
2 |
Прямая лежит в плоскости |
|
2 |
3 |
Прямые параллельна плоскости |
|
3 |
3 |
Прямая пересекается с плоскостью в единственной точке |
|
3 |
4 |
Прямая и плоскость скрещиваются (нет общих точек и не параллельны) |
Две плоскости (k=s=2)
|
r |
R |
примечание |
|
2 |
2 |
Плоскости совпадают |
|
2 |
3 |
Плоскости параллельны |
|
3 |
3 |
Плоскости пересекаются по прямой |
|
3 |
4 |
Плоскости скрещиваются, но имеют параллельные прямые |
|
4 |
4 |
Плоскости пересекаются в единственной точке |
|
4 |
5 |
Плоскости абсолютно скрещиваются (ни какие прямые одной плоскости не параллельны прямым другой плоскости) |
-
Геометрия на плоскости и в пространстве.
Целью данного раздела состоит в рассмотрении таких геометрических понятий как расстояние, площадь, объём с последующим обобщением этих понятий и их переносом на произвольные линейные пространства.
-
Скалярное произведение.
Определение 8.37. Скалярным
произведением геометрических векторов
a и b называется
число, равное произведению длин этих
векторов на косинус угла между ними.
Скалярное произведение векторов
обозначают
![]() .
.
Из определения следует, что длина вектора
равна
![]() .
От
.
От
Приведём свойства скалярного произведения.
-
Симметричность .
-
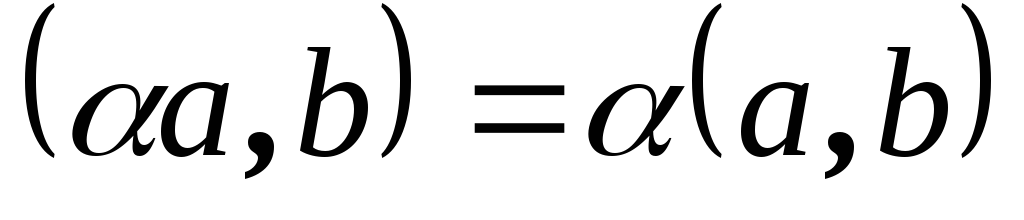
-
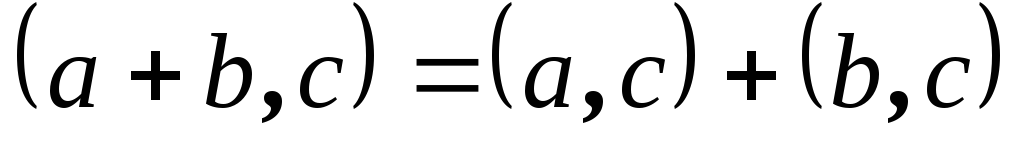
В доказательстве
нуждается только третье равенство. Если
c=0,
то равенство очевидно. Пусть
![]() .
Проекция вектора b
на c
равна
.
Проекция вектора b
на c
равна
![]() .
.
И з
равенства
з
равенства
![]() и приведённой выше формулы выводим
и приведённой выше формулы выводим
![]() .
Приравняем коэффициенты при векторе c
в левой и правой частях равенства
.
Приравняем коэффициенты при векторе c
в левой и правой частях равенства
![]() и умножим на квадрат длины вектора c,
получим свойство 3.
и умножим на квадрат длины вектора c,
получим свойство 3.
Задание длин векторов определяет
скалярное произведение. Действительно,
из свойств скалярного произведения
выводим равенство
![]() ,
которое перепишем в виде
,
которое перепишем в виде
![]() .
Таким образом, задание длин векторов
равносильно заданию скалярного
произведения и наоборот.
.
Таким образом, задание длин векторов
равносильно заданию скалярного
произведения и наоборот.
Выразим скалярное произведение через
координаты перемножаемых векторов.
Пусть
![]() - базис пространства векторов, и
- базис пространства векторов, и
![]() ,
,
![]() - разложения векторов a,b
по этому базису. Тогда по свойствам
скалярного произведения выводим
- разложения векторов a,b
по этому базису. Тогда по свойствам
скалярного произведения выводим
![]()
![]()
![]() .
Обозначим через
.
Обозначим через
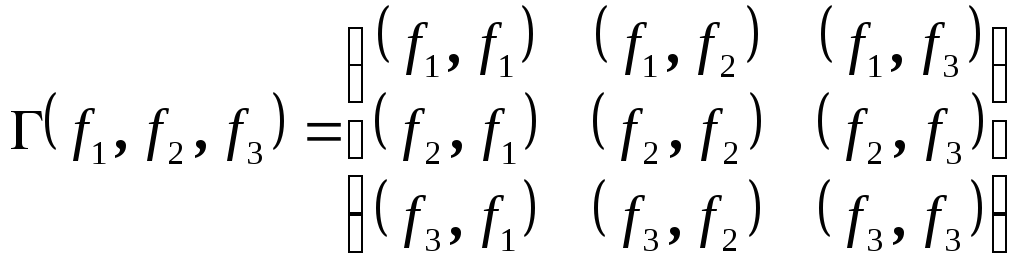 матрицу Грамма от векторов
матрицу Грамма от векторов
![]() ,
составленную из скалярных произведений
этих векторов, через
,
составленную из скалярных произведений
этих векторов, через
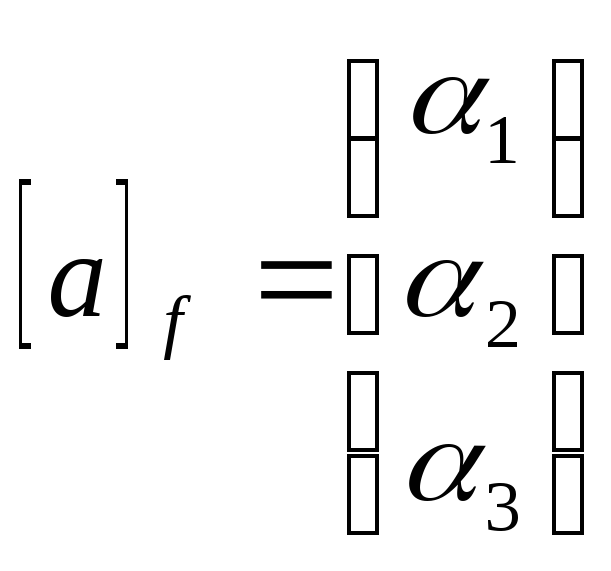 - координаты вектора a в
базисе f. В этих обозначениях
скалярное произведение можно записать
с помощью матричных операций следующим
образом
- координаты вектора a в
базисе f. В этих обозначениях
скалярное произведение можно записать
с помощью матричных операций следующим
образом
![]() .
.
Векторы называются ортогональными
(перпендикулярными) если угол между
ними равен
![]() .
Условие ортогональности векторов
равносильно равенству нулю их скалярного
произведения.
.
Условие ортогональности векторов
равносильно равенству нулю их скалярного
произведения.
Базис
![]() называется ортогональным, если базисные
векторы попарно ортогональны. Матрица
Грамма ортогональной системы векторов
– диагональная. Выражение скалярного
произведения через координаты векторов
в ортогональном базисе принимает более
простой вид, а именно,
называется ортогональным, если базисные
векторы попарно ортогональны. Матрица
Грамма ортогональной системы векторов
– диагональная. Выражение скалярного
произведения через координаты векторов
в ортогональном базисе принимает более
простой вид, а именно,
![]() .
.
В ортогональном базисе скалярное
произведение вектора a
на базисный вектор равно
![]() ,
то есть, координаты вектора a
находятся по формулам
,
то есть, координаты вектора a
находятся по формулам
![]() .
.
Ортогональный базис
![]() ,
в котором длина каждого базисного
вектора равна 1, называется ортонормированным.
В ортонормированном базисе координаты
вектора x определяются
по формулам
,
в котором длина каждого базисного
вектора равна 1, называется ортонормированным.
В ортонормированном базисе координаты
вектора x определяются
по формулам
![]() ,
а скалярное произведение векторов равно
,
а скалярное произведение векторов равно
![]() .
.
