
- •Натуральные числа
- •Метод математической индукции.
- •Бином Ньютона, треугольник Паскаля
- •Целые числа
- •Рациональные числа
- •Числовые кольца, поля
- •Вещественные числа
- •Поле комплексных чисел
- •Комплексная плоскость.
- •Извлечение корней, корни из единицы
- •Делимость многочленов. Наибольший общий делитель. Алгоритм Евклида. Расширенный алгоритм Евклида.
- •Разложение рациональных функций в сумму дробей.
- •Неприводимый многочлен, его свойства
- •Из вытекает, либо , либо .
- •Если неприводимый многочлен делится на неприводимый многочлен, то они отличаются числовым множителем.
- •Корень многочлена.
- •Интерполяционный многочлен
- •Интерполяционный многочлен в форме Лагранжа
- •Интерполяционный многочлен в форме Ньютона
- •Разложение многочлена над полем рациональных чисел
- •Примитивный многочлен, его свойства
- •Критерий Эйзенштейна
- •Все коэффициенты многочлена f(X), кроме старшего, делятся на p
- •Старший коэффициент не делится на p
- •Свободный член не делится на
- •Метод Кронекера разложения многочлена на неприводимые многочлены над кольцом целых чисел.
- •Рациональные корни.
- •Присоединение корня. Поле разложения многочлена.
- •Формальная производная, ее свойства
- •Производные высоких порядков
- •Интерполяционный многочлен Лагранжа-Сильвестра
- •Формулы Виета
- •Симметрические полиномы
- •Формулы Кардано
- •Способ Феррари
- •Дискриминант
- •Основная теорема Алгебры
- •Разложение многочлена на неприводимые множители над полем вещественных чисел
- •Теорема Штурма
- •Любые два соседних многочлена не имеют общих корней
- •Последний многочлен не имеет вещественных корней.
- •Если в окрестностях корня a многочлена сам многочлен возрастает, то , а если убывает, то
- •Метод Гаусса решения системы линейных уравнений
- •Равносильные преобразования
- •Умножение строки не ненулевое число.
- •Перестановка строк
- •Прибавление к некоторой строке другой строки, умноженной на число.
- •Метод Гаусса.
- •Перестановки
- •Четность перестановок
- •Определитель
- •Свойства определителя
- •Изменит знак при перестановке столбцов
- •Равен нулю, если имеется два одинаковых столбца
- •Не изменится при прибавлении к столбцу другого столбца, умноженного на число.
- •Вычисление определителей произвольных порядков
- •Определитель Вандермонда
- •Теорема Лапласа
- •Умножение матриц
- •Формула Бине-Кощи
- •Операции с матрицами
- •Обратная матрица
- •Правило Крамера
- •Матрица элементарных преобразований
- •Построение обратной матрицы
- •Блочные матрицы
- •Алгоритм Штрассена
- •Кронекерово произведение
- •Формула Фробениуса
- •Линейные пространства.
- •. Линейная зависимость. Теорема о замене. Ранг системы.
- •Конечномерные пространства. Базис. Размерность. Дополнение до базиса. Базис суммы, пересечения.
- •. Прямая сумма подпространств. Проекция.
- •Изменение координат вектора при изменении базиса.
- •Изоморфизм линейных пространств.
- •Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.
- •Ранги матрицы.
- •Общее решение системы линейных уравнений.
- •Двойственное пространство
- •Взаимное расположение линейных многообразий в пространстве.
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Симметричность .
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
-
Формула Фробениуса
Пусть матрица A имеет
блочный вид
 .
Припишем к ней справа единичную матрицу
и найдём обратную к матрице A.
Для этого выполним следующие действия:
.
Припишем к ней справа единичную матрицу
и найдём обратную к матрице A.
Для этого выполним следующие действия:
-
Умножим (слева) на матрицу
 (конечно в предположении существования
обратной матрицы). В результате получим
матрицу
(конечно в предположении существования
обратной матрицы). В результате получим
матрицу
 .
. -
Вычтем из второй блочной строки первую, умноженную на матрицу
 (на языке матриц мы умножим слева на
матрицу
(на языке матриц мы умножим слева на
матрицу
 ).
В результате получится матрица
).
В результате получится матрица
 .
. -
Умножим слева на матрицу
 .
В результате получим матрицу
.
В результате получим матрицу

-
Вычтем из первой блочной строки вторую, умноженную на матрицу
 (т.е.
умножим слева на матрицу
(т.е.
умножим слева на матрицу
 ).
В результате получится матрица
).
В результате получится матрица

Тем самым найдена обратная матрица к
матрице A. Формула
 называется
формулой Фробениуса. Использование
формулы Фробениуса позволяет уменьшить
количество арифметических операций
при вычислении обратной матрицы.
называется
формулой Фробениуса. Использование
формулы Фробениуса позволяет уменьшить
количество арифметических операций
при вычислении обратной матрицы.
Обозначим через
![]() и
и
![]() число арифметических операций необходимых,
соответственно, для обращения и умножения
матриц n-го порядка. Имеет
место рекуррентная формула
число арифметических операций необходимых,
соответственно, для обращения и умножения
матриц n-го порядка. Имеет
место рекуррентная формула
![]() .
Положим
.
Положим
![]() ,
тогда при умножении матриц по формулам
Штрассена
,
тогда при умножении матриц по формулам
Штрассена
![]() .
Применив формулу k раз
(учитывая
.
Применив формулу k раз
(учитывая
![]() )
получим
)
получим
![]() .
Подставив вместо k его
выражение через n (
.
Подставив вместо k его
выражение через n (![]() )
получим
)
получим
![]() .
.
-
Линейные пространства.
Определение 7.23Множество V называется линейным пространством над числовым полем P, если определены две операции
-
сложения элементов из V (+)
-
умножения элемента из V на элемент из P (*)
Эти операции удовлетворяют аксиомам:
-
ассоциативность сложения, т.е.
 (x+y)+z=x+(y+z)
(x+y)+z=x+(y+z) -
коммутативность сложения, т.е.
 x+y=y+x
x+y=y+x -
существование 0, т.е.
 x+0=x
x+0=x -
существование обратного
 x+y=0,
обратный обозначают –x.
x+y=0,
обратный обозначают –x. -
ассоциативность умножения

 .
. -
Дистрибутивность
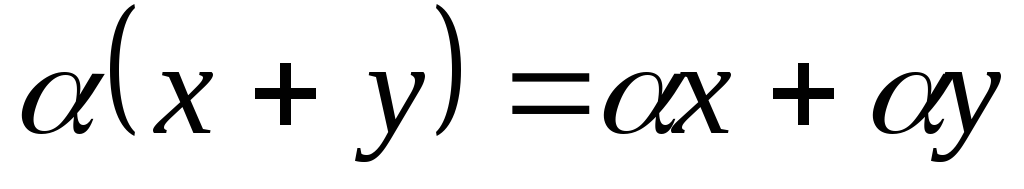
-
Дистрибутивность

-
умножение на 0 0x=0. (в правой части 0 – элемент из V)
-
умножение на 1; 1x=x
Элементы линейного пространства называются векторами, а элементы числового поля P – скалярами.
Примеры линейных пространств.
-
Множество непрерывных функций над R
-
Множество векторов пространства над R
-
Арифметическое пространство (множество наборов из n чисел из P)

Определение 7.24Подмножество W линейного пространства V над полем P называется подпространством, если оно является пространством (в смысле выполняются все аксиомы)
Теорема 7.36. Для того, что бы подмножество W линейного пространства V над числовым полем P являлось подпространством необходимо и достаточно выполнения двух условий:
Примеры подпространств:
-
Множество многочленов образует подпространство в пространстве всех функций.
-
Множество решений системы линейных уравнений Ax=0 в арифметическом пространстве
-
Плоскость, прямая в пространстве векторов.
-
Линейная оболочка системы векторов (то есть множество всех линейных комбинаций векторов)

Следствие 7.15. Пересечение линейных подпространств является подпространством
Доказательство заключается в проверке выполнений условий Теорема 7 .36.
Определение 7.25 Суммой
подпространств V+W
называется множество векторов вида
![]()
Следствие 7.16 Сумма подпространств – подпространство.
Доказательство заключается в проверке выполнений условий Теорема 7 .36.
Следствие 7.17 Сумма подпространств V+W – наименьшее подпространство, которое содержит как V так и W.
Доказательство.
Обозначим через F
подпространство, являющееся пересечением
всех подпространств содержащих
подпространства V
и W.
Так как V+W
содержит оба этих подпространства, то
![]() .
Поскольку F
содержит как V
так и W,
и является подпространством (Следствие 7 .15),
то сумма векторов x+y,
где
.
Поскольку F
содержит как V
так и W,
и является подпространством (Следствие 7 .15),
то сумма векторов x+y,
где
![]() и
и
![]() ,
принадлежит F.
Таким образом, установлено включение
,
принадлежит F.
Таким образом, установлено включение
![]() .
Объединяя включения, получаем равенство
V+W=F.
.
Объединяя включения, получаем равенство
V+W=F.
