50

21.06.2019

Лекции по ГА 1 семестр (спец. Пи)

1. Числа.

   1. Натуральные числа

Определение 1.1Определение натуральных чисел N

1 - натуральное число. Если n - натуральное число, то следующее за ним n+1 так же натуральное число. Если кодировать натуральное число количеством чёрточек, равных этому числу, то под операцией + можно понимать просто приписывание очередной чёрточки. Далее, операция + распространяется на всё множество натуральных чисел. Операция + равносильна приписыванию к одной последовательности чёрточек, обозначающей первое слагаемое, другой последовательности чёрточек, обозначающей второе слагаемое. Отметим свойства данной операции

1. (a+b)+c=a+(b+c) - ассоциативность

2. a+b=b+a – коммутативность

Кроме операции + на множестве натуральных чисел определяется операция *. Операция определяется через сложение . Свойства операции умножения:

1. a*(b*c)=(a*b)*c – ассоциативность

2. a*b=b*a – коммутативность

3. a*(b+c)=a*b+a*c - дистрибутивность

2. Метод математической индукции.

Тот факт, что множество натуральных чисел может быть упорядочено по возрастанию часто используется при доказательстве математических утверждений. Допустим, у нас имеется серия утверждений, пронумерованных натуральными числами A₁,…,A_n… , и установлена истинность утверждения A₁ (основание мат. индукции), а так же показана справедливость посылки A_n-1A_n в предположении истинности утверждений A₁,…,A_n-1 для любого натурального числа n. Выполнение этих условий гарантирует истинность всех утверждений A₁,…,A_n . Для примера покажем справедливость формулы .

При n=1 формула принимает вид , верно. Пусть формула верна для n-1. Покажем её справедливость для n. Следующий пример связан с биномом Ньютона.

1. Бином Ньютона, треугольник Паскаля

Рассмотрим бином (a+b)ⁿ. Если раскрыть скобки, привести подобные, то получившиеся сумма состоит из слагаемых вида aⁱb^n-i с некоторыми числовыми коэффициентами. Например: (a+b)²=a²b⁰+2ab+a⁰b². В общем случае можно записать , где - числовой коэффициент. Из тождества (a+b)ⁿ=(a+b)(a+b)^n-1 выводим равенства и , которые позволяют строить треугольник Паскаля. Приведём первые его 4 строки 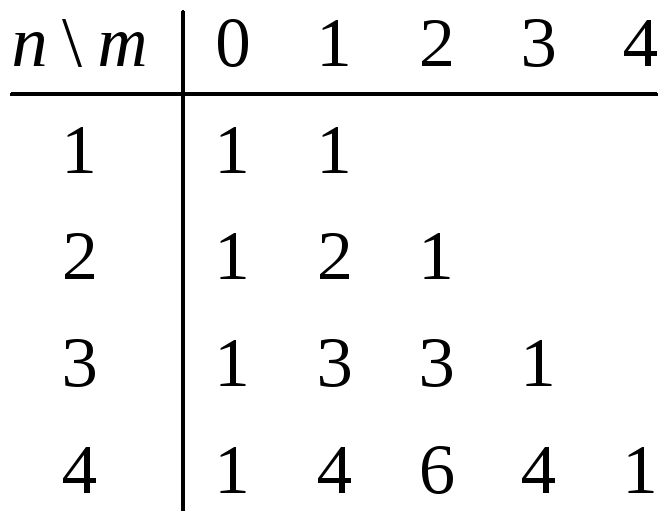. Число, расположенное в треугольнике Паскаля на пересечении строки n и столбца m, равно

• 1, если m=0, или m=n,

• сумме элементов предыдущей строки, расположенных в столбцах m и m-1, если .

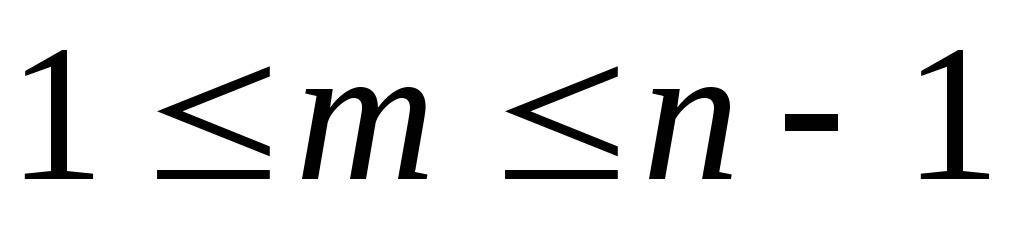Таким образом, элементы треугольника Паскаля суть биномиальные коэффициенты. В частности .

Обозначим через произведение натуральных чисел от 1 до n. Для удобства обозначений положим .

Теорема 1.1 Биномиальный коэффициент вычисляется по формуле .

Доказательство проводится индукцией по n. При n=1 утверждение очевидно. Пусть оно верно при n-1. Покажем его справедливость для n. Если m=0, то . Если m=n, то . Если , то . По предположению индукции . Теорема доказана.

3. Целые числа

Решение уравнений вида a+x=b приводит к получению целых чисел Z. При этом следует отметить, что уравнение a+c+x=b+c имеет то же самое решение. На множество целых чисел естественным образом переносятся операции + и *, обладающими теми же самыми свойствами.

4. Рациональные числа

Решение уравнений вида a*x=b (a0) приводит к получению рациональных чисел Q. Уравнение a*c*x=b*c имеет то же самое решение. На множество рациональных чисел естественным образом переносятся операции + и *.