20. Существ. Интеграла Лебега.

Теорема: Инт. Лебега от ограниченной измеримой ф-ии f(x) определяемой на измеримом м-ве Е существует по этому мн-ву (без док-ва). Заметим, что инт. Лебега может быть рассмотрен по определению если ф-ия f(x) ограничена и измерима на мн-ве Е. и согластно данной теореме интеграл от неё существует (т.е для какой ф-ии инт.Лебега определён, для такой ф-ии инт.Лебега и существует). Теория интеграла Римана менее совершенна т.к. интеграл Римана берётся для ограниченных ф-ий, но класс ф-ии для которых интеграл Римана существует чётко не обозначен. Нами были сформулированы некоторые достаточные условия (непрерывности ф-ии, существование конечного мн-ва точек разрыва и т.д.). заметим, что класс ф-ии интергируемых по Риману может быть записан чётко в терминах инт.Лебега.

21. Интеграл Лебега и Римана.(сравнение)

Пусть на измеримой мн-ве Е дана измеримая ограниченная функция f(x), что m<=f(x)<=M. В отличии от построения интегральной суммы Римана, здесь мы будем разбивать на части не мА-ва, на к-ом определена ф-ия,а на значения (отрезок) в к-ый входят все значения ф-ии. Разобъём [m,M] на части =М. Составим интегральную сумму Лебега S= где - это мера такой части Е, на к-ой выполняется указанное 2ое нер-во, причём эта часть мн-ва Е ял. Измеримым мн-вом т.к. ф-ия f(x) измерима по условию. Обозначим через максимальную разность . Теория интеграла Римана менее совершенна т.к. интеграл Римана берётся для ограниченных ф-ий, но класс ф-ии для которых интеграл Римана существует чётко не обозначен. Нами были сформулированы некоторые достаточные условия (непрерывности ф-ии, существование конечного мн-ва точек разрыва и т.д.). заметим, что класс ф-ии интергируемых по Риману может быть записан чётко в терминах инт.Лебега.

22.Срезка неотр. Ф-ии и её св-ва. Суммируемые неотрицательные ф-ии. Суммир-ые ф-ии любого знака.

Понятие инт.Лебега можно обобщить на случаи неогранич.ф-ии, укажем идею такого обобщения. Будем рассматривать неограниченные и неотриц. Измеримые ф-ии. Назовём ф-ию [f(x)]_N срезкой ф-ии f(x), к-ая определяется следующим образом

[f(x)]_N = 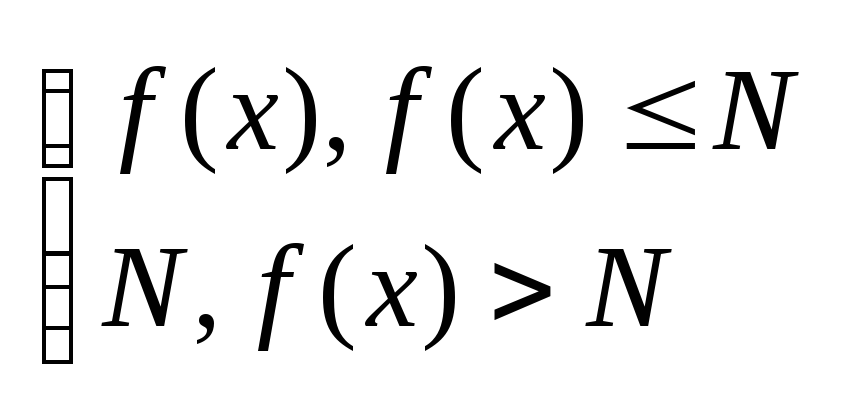. если этот предел существует ,то его наз-ют интегралом Лебега от неограниченной неотриц. Ф-ии. Если , где f(x) неогран. Неотриц. Ф-ия существует, то ф-ия f(x) наз-ся суммируемой ф-ией. Мн-во всех суммируемых на отрезке [a,b] ф-ии образует пространство L1. оно Явл. Метрическим, если ввести расстояние между ф-иями f1(x), f2(x),

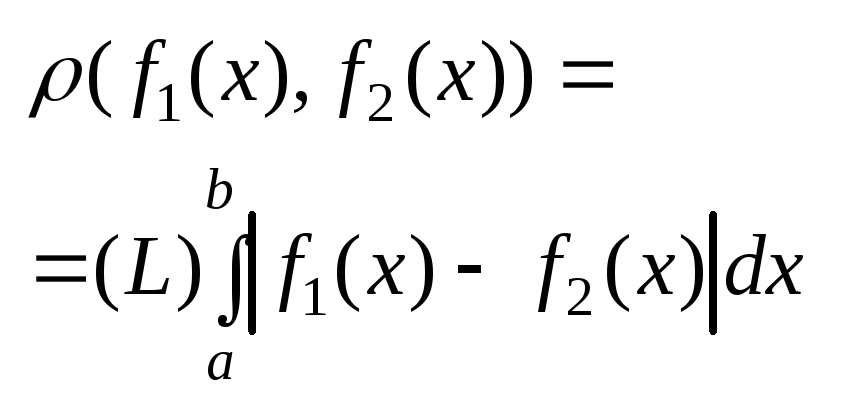. Рассмотрим случай инт.Лебега для неогран. Ф-ии произвольного знака. Введём в рассмотрение 2е вспомогательные ф-ии

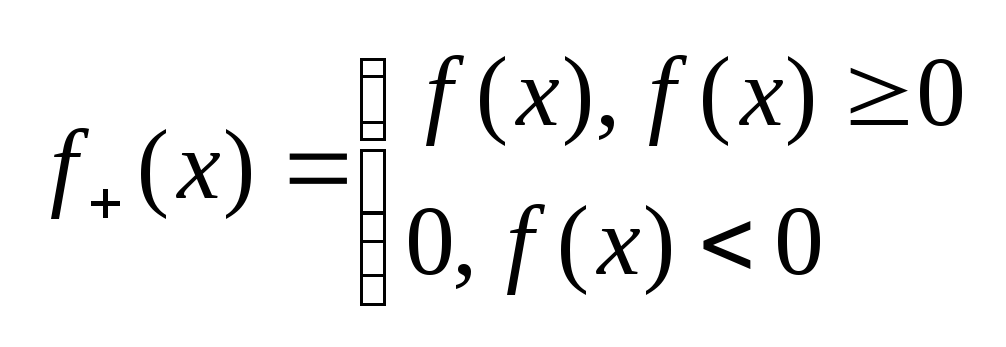
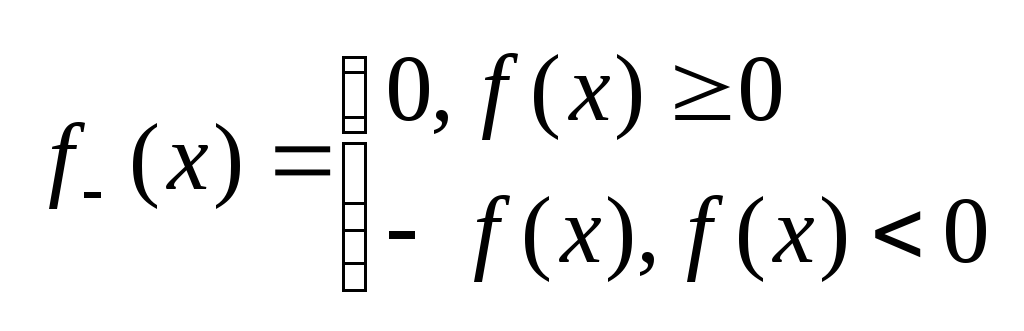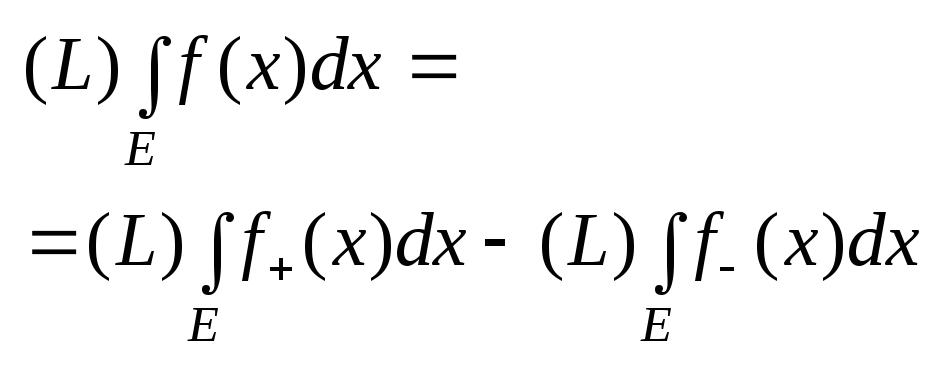; тогда инт.Лебега где f(x) – неогран. Ф-ия произвольного знака.

23. Сходящиеся и фундаментальные последовательн. Метрических пространствах и их связи. Полные метрические пространства.

Примеры. во мн-ве R всякое фундаментальная последовательность действител. Чисел Явл. Сходящейся. Необходимо определить понятие сходящейся послед. 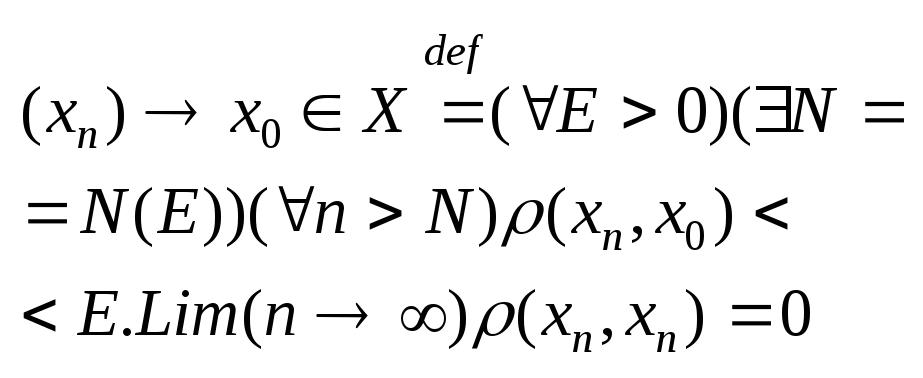. Послед-ть точек метрического простр. Имеющая предел наз-ся сходящейся. Последовательность (xn) точек метрического простр. Наз-ся фундаментальной, если другими словами с ростом номеров члены данной последов. Неограниченно приближаются друг к другу. . Опр. Метрическое пространство М наз-ся полным, если в нём каждая фундаментальная последовательность сходится к точке этого пространства. М – полное метрическое пространство по определению (xn) – фундаментальная следует . Легко убедиться, что для полного пространства М имеет место критерий Коши (необх. И дост. Условие сходимости последовательности точек метрического пространства). Критерий Коши: послед точек полного метрического пространства сходится т. И т. Т., когда она фундаментальна. Пример:Можно показать пользуясь указанным определением,что пространство R, полные.