18. Интеграл Римана. Теорема Лебега. Примеры.

Пусть функция определена и неограниченна на сегменте . Разобьем сегмент произвольным образом на части точками деления . Обозначим через наибольшую из разностей . Выберем в каждом из промежутков произвольную точку и составим сумму:

Если существует предел суммы , при не зависящий от способа разбиения сегмента и от выбора точек , то этот предел называется интегралом Римана функции в промежутке от до и обозначается .

Т.(Либега): Для интегрируемости по Риману ограниченной функции на отрезке необходимо и достаточно чтобы множество точек разрыва имело Либегову меру равную 0 (без доказательства).

Как следствие из этой теоремы вытекает следующее утверждение об интегрируем. по Риману ограниченной функции имеющей счетное множество точек разрыва.

Т.: Если функция интегрируема по Риману, то она будет интегрируема и по Либегу и справедлива формула, которая показывает, что эти интегралы будут совпадать (без доказательства).

С теоретической точки зрения эта теорема показывает, что класс функций интегрируем по Либегу, не уже чем класс интегрируемый по Риману. В действительности он оказался шире и чтобы убедиться в этом, достаточно привести хотя бы 1 пример функции не интегрируемой по Риману.

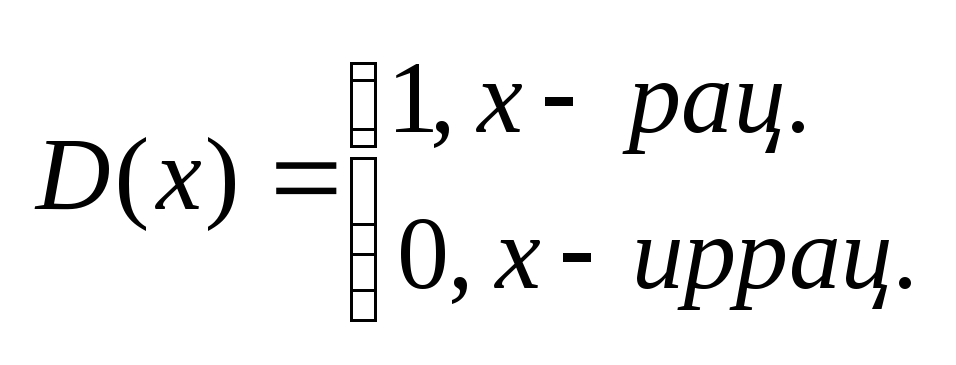на

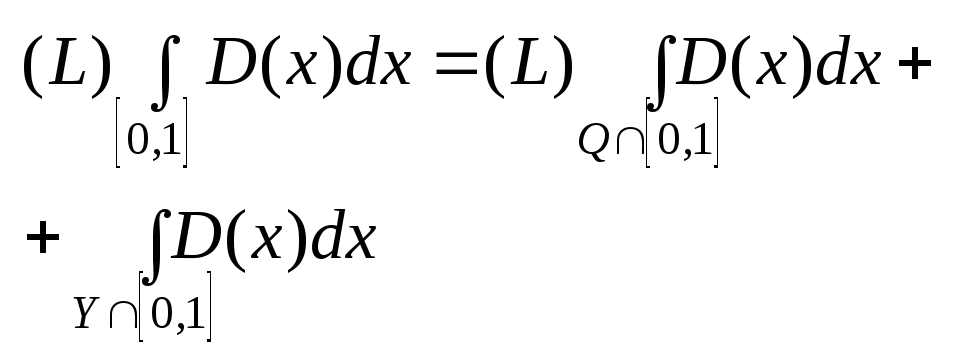Но функция Дерихле по Риману не дифференцируема т.к. она разрывна в каждой точке отрезка, а значит мера множеств точек разрыва равна

19. Интеграл Лебега и его свойства.

Пусть на измеримом мн-ве Е дана измеримая ограниченная функция f(x). f(x)-ограниченна (сущ. m,M), что m≤f(x)≤M, f(x) принадлежит [m,M]

В отличие от построения интегральной суммы Римана здесь мы будем разбивать на части не мн-во, на котором определена функция, а (значение) отрезок, в который входят все значения функции. Разобьем отрезок [m,M] на части

m=y₀<y₁<…<y_i<y_i+1<…<y_n=M

Составим интегральную сумму Лебега

S=∑ y_i mЕ(y_i≤f(x)< y_i+1

mЕ(y₁≤f(x)< y_i+1)–мера такой части мн-ва Е, на которой выполняется указанное двойное нер-во, причем эта часть мн-ва Е явл. измеримым мн-ом т.к. функция f(x) измерима по условию.

Обозначим через λ-максимальную разность |y_i+1-y_i|

Опр Если предел lim S сущ., конечен и не зависит от способа разбиения отрезка [m,M] на части то он наз. интегралом Лебега от функции f(x) на мн-ве Е: (L)∫f(x)dx, а функция f(x) интегрируемой по Лебегу на мн-ве Е. Если Е=[a,b], то (L)∫f(x)dx (интеграл от а до b)

Замечание Вся теория интеграла Лебега (внешний вид) походит на внешний вид теории интеграла Римана. Если вспомнить общую конструкцию построения интеграла Римана, то можно легко вспомнить, сравнить и определить сходства интеграла Лебега и интеграла Римана.

Св-ва интеграла Лебега

1° Интеграл Лебега по мн-ву Е от функции f(x)dx=0 ((L)∫f(x)dx=0) если мера мн-ва Е=0

2° Если функция f(x) заключена в пределах от А до B (А≤f(x)≤B), то для любого Е имеем след нер-во: A·m·E≤(L)∫f(x)dx≤B·m·E

3° Если Е₁ƯЕ₂=Е, Е-измеримое мн-во, при чем Е₁∩Е₂ ≠ Ø, то (L)∫f(x)dx (по Е)=(L)∫f(x)dx (по Е₁)+(L)∫f(x)dx (по Е₂)

Замечание Из св-в 1и 3 можно заключить, что значение интеграла Лебега не изменится, если произвольным образом изменить значение подынтегральной функции на некотором подмн-ве мн-ва Е имеющем нулевую меру

4° Константу можно выносить за знак интеграла

5° Интеграл суммы равен сумме интегралов

6° Если для любого xE, f(x)≤g(x), то интеграл от f(x) ≤ интегралу от g(x)

7° Модуль интеграла Лебега функции f(x) ≤ интегралу функции по модулю