16. Измеримые функции. Свойства измеримых функций.

Опр Функция y=f(x) действительного переменного определенная на измеримом мн-ве Е наз. измеримой если для любого действительного числа Е(f(x)>А)-измеримо

Т.е. y=f(x) измеримо если:

1) Е=D_f -измеримо

2) Е(f(x)>А)-измеримо для любого А

Обозначение Е(f(x)>А) означает такое подмн-во мн-ва Е, для которого выполнено нер-во в скобках

Из опр. ясно, что функция, определенная на мн-ве нулевой меры всегда измерима. Если функция y=f(x) измерима на мн-ве Е, то она будет измерима и на любом измеримом подмн-ве мн-ва Е.

Е₁cЕ

Е₁(f(x)>А)-измеримо

f(x)-измеримо на Е → Е(f(x)>А)-измеримо, т.к. по условию f(x)-измеримо на Е

Замечание В опр. измеримой функции можно будет использовать другие нер-ва: Е(f≥А), Е(f<А), Е(f≤А)

Обоснуем это: Е(f≥А)=∩Е(f>А-1/k), Е(f<А)=СЕ(f≥А), Е(f≤А)=СЕ(f>А)

Функция y=f(x) определенная и непрерывная на замкнутом мн-ве F измеримо

f(x)-опр. и непр. F, F-замкнуто, следовательно f(x)-измерима.

Для любого А, (f(x)>А)-измеримо

Достаточно показать, что мн-во замкнуто

CF(f(x)≥А)=F(f(x)<А)

ζCF(f≥А)

ζCF(F<А)

По условию функция непрерывна, значит в некоторой окрестности точки ζ будет выполняться нер-во f(x)<А, следовательно, в окрестности точки ζ нет ни одной точки из мн-ва F(f(x)≥А). Точка ζ не явл. предельной точкой мн-ва F(f(x)≥А). В силу произвольности точку ζ, получили, что ни одна точка из дополнения не будет предельной для нашего мн-ва, следовательно, наше мн-во будет содержать все свои предельные точки и оно будет замкнутым и следовательно измеримым.

f(x)=const-измерима на любом измеримом мн-ве Е

Св-ва измеримых функций:

1° Если функций y=f(x)-измерима, то будут измеримы и функции f(x)·k, f(x)+k, f²(x)

Если функция y=f(x) измерима на мн-ве Е, то Е(f(x)+k>A)=E(f(x)>A-k)=E(f(x)>A*)

f(x)+k-измеримы

2° Если функции f(x) и g(x) измеримы на мн-ве Е, то на этом мн-ве будут измеримы и функции f(x)+g(x), f(x)-g(x), f(x)/g(x) (g(x)≠0)

Вопрос 17.

Измеримость мн-в: Е(f≥A), E(f<A), E(f≤A),Е(f>g).

Ф-ия y=f(x) дейст. переменного опр-ая на измеримом мн-ве Е, наз-ся измеримой, если для любого действ. А мн-во E(f(x)>A) - измеримо. Т.е. y=f(x) – изм.: 1) Е=D_f-изм; 2) для любого А, E(f(x)>A) – измеримо. В опр-ии E(f(x)>A) означает такое подмн-во мн-ва Е, для которого вып-мо нер-во находящееся в скобках. Из опр-ия ясно, что ф-ия опр-ая на мн-ве нулевой меры будет всегда измеримо. Рис. Также следует, что если ф-ия изм-а на мн-ве Е, то она будет изм-ма и на любом измеримом подмн-ве мн-ва Е.

Из f(x)-изм на Е следует, что E(f(x)>A)-изм. E(f(x)>A)-изм. По ус-ию, f(x)-изм. на Е, Е₁-изм, т.к. . Замечание: в опр-ии ф-ии м.б. исп-ть другие нер-ва: Е(f≥A), E(f<A), E(f≤A). Обоснование:

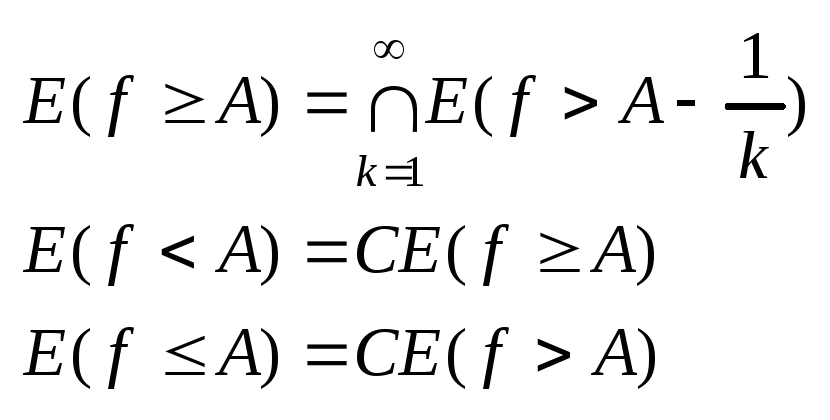
Примеры. 1) Функц y=f(x) –опред и непр.на замкнутом мн-ве F – измерима. => f(x) – изм. Для любого А: F(f(x)>A) – изм. Обоснование. Дост.показать, что мн-во F(f(x)≥A) замкнуто. (F(f(x)≥A))=F(f(x)<A). ξCF(f(x)≥A) = ξF(f(x)<A). По усл.функция y=f(x) непр. Значит в нек.окр-ти точки ξ будет вып-ся нер-во f(x)<A. След-но, в окр-ти т. ξ нет ни одной точки из F(f(x)≥A). Т.е. т. ξ не явл-ся предельной точкой мн-ва F(f(x)≥A). В силу произвол-ти точки ξ получили, что ни одна точка из дополнения не будет предельной для нашего мн-ва. Поэтому наше мн-во будет содержать все свои пред.точки, поэтому оно замкнуто, а значит измеримо. F(x) измерима на F.

2) f(x)=const измерима на любом измеримом мн-ве. E(f(x)>A) – изм. y=C (график). E(f(x)>A) = 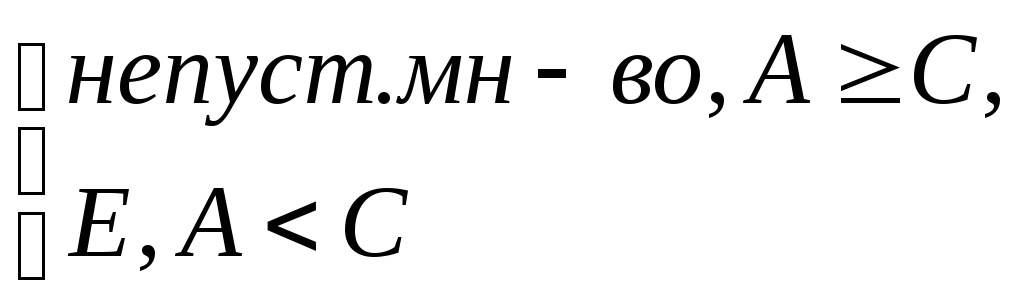E(f(x)>A) –изм. => они изм.