
- •Понятие мощности мн-ва.
- •7. Классификация точек и мн-в в метр.Пр-ве.
- •8 Связь между замкнутыми и открытыми множествами.
- •9. Операции над открытыми и замкнутыми множествами.
- •10. Структура открытых, замкнутых и совершенных множ. На прямой.
- •11. Канторово множ и его свойства.
- •12.Понятие о ф-ии с ограничен изменением. Понятие спрямляемой кривой.
- •13. Внешняя и внутренняя меры Лебега линейных множеств и их свойства.
- •14.Измеримые множ. Примеры множеств нулевой меры. Измеримость дополнения измеримого множ. Действия над измеримыми множ.
- •16. Измеримые функции. Свойства измеримых функций.
- •Вопрос 17.
- •18. Интеграл Римана. Теорема Лебега. Примеры.
- •19. Интеграл Лебега и его свойства.
- •20. Существ. Интеграла Лебега.
- •21. Интеграл Лебега и Римана.(сравнение)
- •22.Срезка неотр. Ф-ии и её св-ва. Суммируемые неотрицательные ф-ии. Суммир-ые ф-ии любого знака.
- •23. Сходящиеся и фундаментальные последовательн. Метрических пространствах и их связи. Полные метрические пространства.
- •24. Отображение метрических пространств.
- •25.Связные множества. Свойства непрерывных отображений связных множеств.
- •26.Сжимающие отображения. Т Банаха.
- •27. Применение принципа сжимающих отображений.
- •28.Линейные нормированные и гильбертовы пространства. Пространство функций, суммируемых по Лебегу.
- •29. Ортогональные системы.
- •30. Ряд Фурье. Экстремальное свойство частичных сумм ряда Фурье.
- •33. Полнота ортогональной системы и ее связь с замкнутостью
- •34. Уравнение свободных колебаний.
27. Применение принципа сжимающих отображений.
Принцип сжимающих отображений может использоваться при доказательстве существования и единственности решения уравнений разных типов. Рассмотрим примеры.
1.
Пусть дано уравнение F(x)=0,
![]() .
Формально его можно переписать в виде
x=f(x),
где f(x)=x+F(x).
Предположим, что для f
выполнено условие
Липшица:
.
Формально его можно переписать в виде
x=f(x),
где f(x)=x+F(x).
Предположим, что для f
выполнено условие
Липшица:
![]() ,
где
,
где
![]() и 0<k<1
(оно заведомо имеет место, например,
если f
– дифференцируема и
и 0<k<1
(оно заведомо имеет место, например,
если f
– дифференцируема и
![]() ).
По предыдущей теореме существует
единств. неподвижная точка x0
для оператора f,
т.е. решение для уравнения F(x)=0.
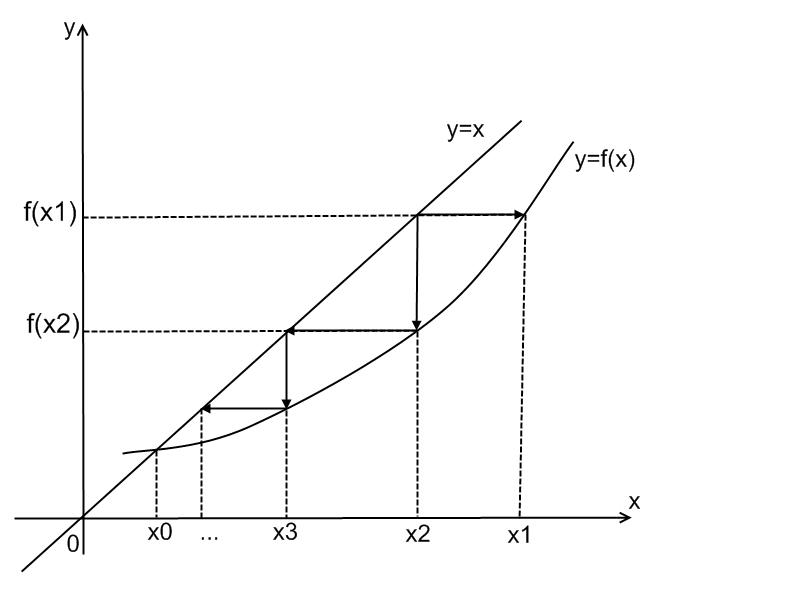
К этому решению можно построить
последовательные
приближения,
начав с произвольного x1.
Затем находим x2=f(x1),
x3=f(x2)
и т.д.: (xn)->x0
).
По предыдущей теореме существует
единств. неподвижная точка x0
для оператора f,
т.е. решение для уравнения F(x)=0.
К этому решению можно построить
последовательные
приближения,
начав с произвольного x1.
Затем находим x2=f(x1),
x3=f(x2)
и т.д.: (xn)->x0
2.
Рассмотрим
док-во теоремы о существовании неявной
ф-ции.
Пусть дан f(чбн)
определена для
![]() и
и
![]() ,
непрерывна
по
x
и имеет производную
,
непрерывна
по
x
и имеет производную
![]() удовлетворяющую неравентсву:
удовлетворяющую неравентсву:
![]() .
Тогда уравнение f(x,y)=0
имеет
единственное непрерывное
решение y=y0(x)
на [a,b].
Рассмотрим в простр. C[a,b]
оператор
.
Тогда уравнение f(x,y)=0
имеет
единственное непрерывное
решение y=y0(x)
на [a,b].
Рассмотрим в простр. C[a,b]
оператор
![]() .
Его неподв. точка y0(Ay0=y0),
очевидно, будет решением уравнения
f(x,y)=0.
Поэтому достаточно убедиться, что
применима теорема Банаха. Пусть y1(x),
y2(x)
.
Его неподв. точка y0(Ay0=y0),
очевидно, будет решением уравнения
f(x,y)=0.
Поэтому достаточно убедиться, что
применима теорема Банаха. Пусть y1(x),
y2(x)![]() C[a,b].
Тогда
C[a,b].
Тогда
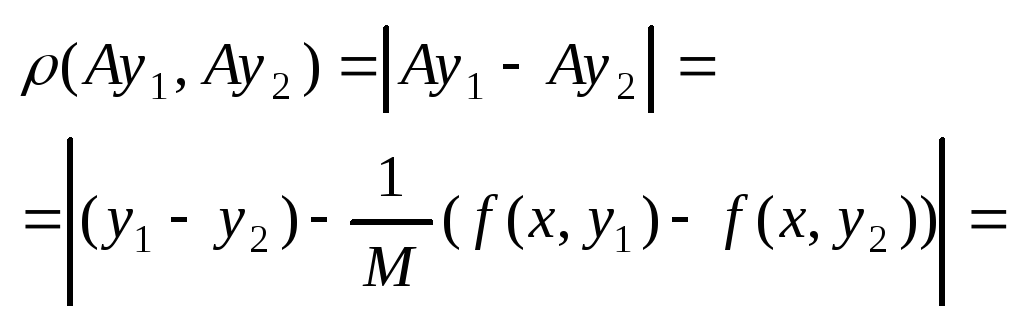
![]()
![]() ;
;
![]() .
Здесь применена теорема Лагранжа;
.
Здесь применена теорема Лагранжа;
![]() и
и
![]() .
Таким образом, A
– сжимающий оператор. И по теореме
Банаха существ. единств. неподвижная
точка y=y0(x).
Это неявная
ф-ция, заданная равенством f(x,y)=0.
Замечание.
Таким
же методом можно доказать теорему в
случае, когда аналогичные условия для
f(x,y)
выполнены в некоторой окрестности т.
(x0,y0),
где f(x0,y0)=0.
Тогда класс функций y=y(x)
подчиняется дополнительному условию:
y0=y(x0)
.
Таким образом, A
– сжимающий оператор. И по теореме
Банаха существ. единств. неподвижная
точка y=y0(x).
Это неявная
ф-ция, заданная равенством f(x,y)=0.
Замечание.
Таким
же методом можно доказать теорему в
случае, когда аналогичные условия для
f(x,y)
выполнены в некоторой окрестности т.
(x0,y0),
где f(x0,y0)=0.
Тогда класс функций y=y(x)
подчиняется дополнительному условию:
y0=y(x0)
28.Линейные нормированные и гильбертовы пространства. Пространство функций, суммируемых по Лебегу.
Опр.:
непустое множество L наз. линейным,
если оно удовлетворяет след. требованиям:
А. для любых двух элементов х, у![]() L однозначно определяется элемент z
L однозначно определяется элемент z![]() L
называемый его суммой, причем:
1.х+у=у+х(коммут) 2. х+(у+z)=(х+у)+z(ассоц)
3.сущ.такой Эл-т 0, что х+0=х для всех
х
L
называемый его суммой, причем:
1.х+у=у+х(коммут) 2. х+(у+z)=(х+у)+z(ассоц)
3.сущ.такой Эл-т 0, что х+0=х для всех
х![]() L(сущ-е
нуля) 4.для числа α и
L(сущ-е
нуля) 4.для числа α и
![]() опред.эл-т
(-х), что х+(-х)=0(сущ.против).В. для
опред.эл-т
(-х), что х+(-х)=0(сущ.против).В. для![]() числа
α и
числа
α и
![]() определ.эл-т
определ.эл-т
![]() (произвед.эл-т
на число), причем:
(произвед.эл-т
на число), причем:
1.
![]()
2.1*х=х
3.![]() 4.
4.![]()
Опр.:
функционал (обознач.![]() )
в лин. простр. L
наз. Нормой,
а пространство L-нормированное,
если для люб. х, у
)
в лин. простр. L
наз. Нормой,
а пространство L-нормированное,
если для люб. х, у![]() L и числа α: а)
L и числа α: а)![]() ,причем
,причем
![]() только
при х=0; б)
только
при х=0; б)
![]() ;
в)
;
в)![]() .
.
Опр.: пространство наз. линейно-нормированным, если оно явл. линейным и в нем определена норма.
Координатное
пространство Гильберта L2 определяется
как множество чмсловых последовательностей
х(х1,х2,…), для которых ряд
![]() сходиться; метрика определяется так же
как и в евклидовом пространстве: если
х(х1,х2,…) и y(y1,y2,…)
суть точки гильбертова пространства,
то
сходиться; метрика определяется так же
как и в евклидовом пространстве: если
х(х1,х2,…) и y(y1,y2,…)
суть точки гильбертова пространства,
то
![]() .
.
Опр.:
назовем ф-ю
![]() срезкой которая опред. след. обр.:
срезкой которая опред. след. обр.:
![]()

![]() Если
этот предел существует,то его называют
интегралом Лебега от неограниченной,
неотрицательной функции. Опр.: если
Если
этот предел существует,то его называют
интегралом Лебега от неограниченной,
неотрицательной функции. Опр.: если
![]() ,
где f(x) – неогр., неотр., ф-я, существует,
то ф-я f(x) называется суммируемой ф-ей.
Множество всех суммируемых на отрезке
АВ ф-й, образует пространство L1,
оно является метрическим. Если ввести
расстояние между ф-ями f1(x)
и f2(x):
,
где f(x) – неогр., неотр., ф-я, существует,
то ф-я f(x) называется суммируемой ф-ей.
Множество всех суммируемых на отрезке
АВ ф-й, образует пространство L1,
оно является метрическим. Если ввести
расстояние между ф-ями f1(x)
и f2(x):
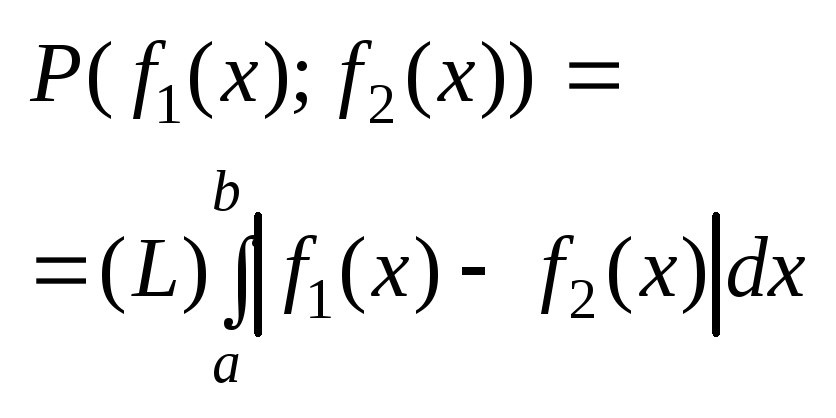 .
.
Опр.:
2 ф-ии называются совпадающими, если
они отличаются др от др, на множестве
меры 0. можно обощить определение
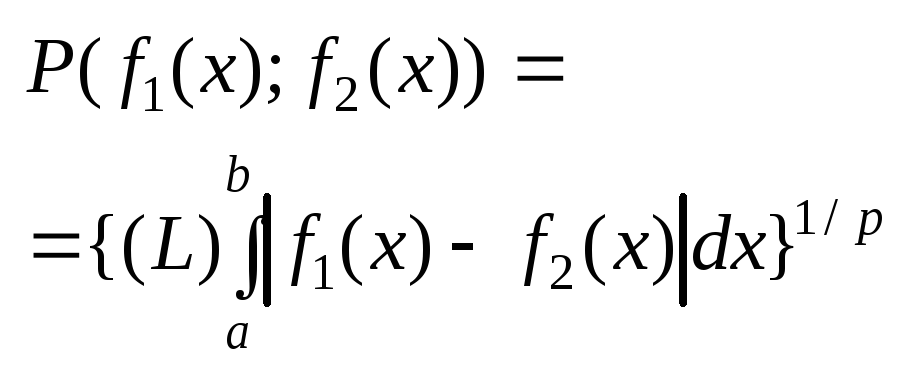 .
Возникает пространство Lp
– метрическое пространство, р>=1. Это
пространство ф-ии, для которых
.
Возникает пространство Lp
– метрическое пространство, р>=1. Это
пространство ф-ии, для которых
![]() - суммируем по Лебегу. Особый интерес
представляет пространство для которого
р=2, т.е. L2
– пространство ф-й, суммируемых с
квадратом. (L2
- суммируем по Лебегу. Особый интерес
представляет пространство для которого
р=2, т.е. L2
– пространство ф-й, суммируемых с
квадратом. (L2![]() ).
Заметим что L2 является подмножеством
L1
( т.к.
).
Заметим что L2 является подмножеством
L1
( т.к.
![]() ).
заметим что Lp,
где р>=1 является полным (т.е. всякая
фундаментальная последовательность
сходится).
).
заметим что Lp,
где р>=1 является полным (т.е. всякая
фундаментальная последовательность
сходится).
