1. Понятие мощности мн-ва.

Опр-ие: если между двумя мн-ми А и В можно установить (сущ-ет взаимно однозначное соот-ие), то эти мн-ва наз-ся эквивалентными. Т.е имеющими одинаковую мощность (или равномощными). Обозначение: А~В.

Опр-ие: отображение f: АВ наз-ся взаимнооднозначным соответствием если для любого найдется один элемент , такой что =у.

Очевидно, что это отношение явл-ся отношением эквивалентности, поэтому оно обладает свойствами:

1. рефлексивности А~А

2. симметричности А~ВВ~А.

3. транзитивность (А~В)и(В~С) (А~В) .

благодаря этому отношению всевозможные мн-ва распадаются на непересекающиеся классы эквивалентности (в один класс попадают все эквивалентные между собой мн-ва) классы эквивалентности можно обозначить (т.е каждому классу эквивалентности можно приписать) специальный символ который называется мощностью.(координатным числом) т.о что мощность мн-ва А трактуется и как класс эквив-ти в который входит мн-во А, и как св-во принадлежности мн-ва А этому классу.

Приписав символ к классу эквивалентности в который входит мн-во натуральных чисел N, мы обнаружим, что мн-во так же входит в этот класс т.е мн-во можно также использовать символ так как N~. Для обозначения мощ-ти мн-ва, вводится символ ==.

2. Счетные мн-ва и их св-ва. Счетость мн-ва Q всех рациональных чисел.

Опр-ие: мн-ва эквивалентные мн-ву натуральных чисел наз-ся счетными. Счетными явл-ся такие мн-ва все элементы которых можно расположить в последовательность (бесконечную) т.е занумеровать, истратив на нумерацию все натуральные числа. Т.о из предыдущего ясно, что мощность чсетного мн-ва обозначается символом .

Примеры: 1. мн-во четных натуральных чисел ~Nпо опр-ию счетное значит мощность =.

2.мн-во членов любой последовательности счетно.

3.мн-во всех целых чисел счетно. Убедиться в этом можно способом нумерации всех целых чисел это можно сделать например так: …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …

9, 7, 5, 3, 1, 2, 4, 6, 8.

Мощность целых чисел .

Замечание, мн-во рациональных чисел счетно. Док-во: рассмотрим сначала , q, q=, m,n . Каждому рац числу q введем характеристику h=m+n, значит h=2;3;4;…

h= 2:1: h= 3:2: h = 4:; 3;1 h = …..

будем попорядку выписывать рациональные числа h пропуская только те из них, которые выписаны нами на предыдущем шаге, т.о каждому значению h будет соответствовать не более чем конечное число рациональных чисел, и так, мы попорядку не пропустив не одного положительного рационального числа сможем выписать в последовательность все положительные рациональные числа. Далее используя способ нумерации как бы применен при доказательстве счетности мн-ва целых чисел получим, что q= .

Св-ва счетных мн-в:

1. счетное мн-во минимальное по мощности среди всех бесконечных мн-в или изо всякого бесконечного мн-ва можно извлечь счетное подмн-во. Док-во: пусть А – произв бесконечное мн-во, выберем из этого мн-ва какой то один элемент и припишем ему номер 1. назовем его , в остальной части мн-ва выберем второй элемент 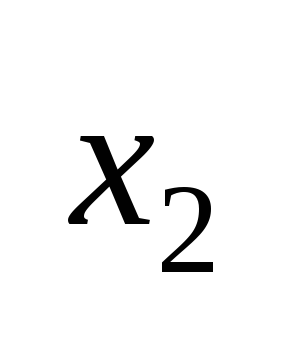, и т.д. будем продолжать этот процесс бесконечно и на нумераию истратим все мн-во натуральных чисел N. В конечном итоге окажется, что в рез-те этой процедуры, все бесконечное мн-во было счетным (т.е мы выбрали все Эл-ты мн-ва) сл-но бесконечное мн-во А содержало счетное подмн-во. Св-во доказано

2. если бесконечное мн-во счетно, то всякое бесконечное подмн-во его так же счетно. Или всяко бесконечное подмн-во счетного мн-ва счетно. Док-во: любое счетное мн-во можно представить в виде последовательности тогда любое бесконечное подмн-во данного счетного мн-ва будет подпоследовательностью. По определению счетного мн-ва подмн-во так же будет счетным.

3. сумма (обьединение) конечного или счетного мн-ва счетных мн-в счетно. +=

+…+=

+…=

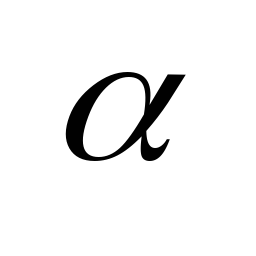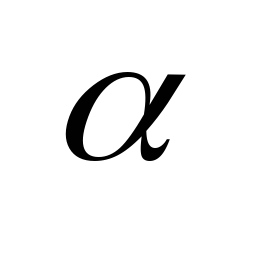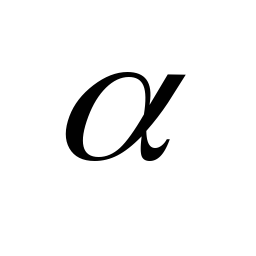
Док-во: достаточно элементы указанных мн-в расположить в последовательность, это можно сделать например способом по «диагоналям» или способом по «квадратам» дано: счетное мн-во , док-ть , -счетно. Выпишем элементы мн-в сл образом, как указано в схеме. (Пропустить место и вписать самостоятельно).

Способ нумерации элементов (записи элементов последовательности) можно усмотреть из приведенной выше схемы, а в зависимости от того конечная или счетная мн-ва мн-в мы будем двигаться по схеме, только вправо до бесконечности или вниз и вправо до бесконечности. Св-во доказано.

Следствие, алгебраических чисел, счетное мн-во.

Опр-ие: алгебраическим числом наз-ся действительные корни уравнения вида:

с целыми коэффициентами ,

Все числа r равны алгебраические.

Действительные числа не явл-ся алгебраическими наз-ся транциндентными.

4. если к бесконечному мн-ву присоеденить конечное или счетное мн-во то его мощность не изменится. А бесконечное мн-во. К это конечное или счетное мн-во. А\=А-.

Следствие, если из бесконечного мн-ва удалить конечное или счетное подмн-во, то его мощность не изменится.

Замечание 1. т.о мощность счетного мн-ва вклассе мощностей бесконечных мн-в выступает в качестве своеобразного нуля.)( - плеор нуль.

Замечание 2. всякое бесконечное мн-во имеет эквивалентные ему собственное подмн-во.

это св-во принципиально отличает бесконечное мн-во от конечного оно может быть взято в качестве определения бесконечного.

3.Несчётность мн-ва всех действ-х чисел отрезка [0,1]. Т: Мн-во действ.чисел отрезка [0,1]несчётно. Док-во методом от противного: предположим, что мн-во действ-х чисел этого отрезка счётно, тогда его м.представить в виде послед-ти. Противоречие б. достигнуто тем, что найдётся хотя бы одна точка х, принадлежащая [0,1], х не (х_n). Пусть все действ.числа отрезка [0,1] расположениы в последоват-ти (х_n). Представим отрезок [0,1]как объединение отрезков [0;1/3][1/3;2/3][2/3;1]. Выберем из 3-х отрезков тот, кот.не содержит 1-й член последоват-ти (х_n), х₁.Выбранный отрезок вновь разделим на 3 равные части. И на этом шаге выберем такой отрезок, который не содержит х₂ и т.д. Продолжим беск.кол-во раз. В рез=те возникает последоват-ть отрезков n, вложенных друг в друга, с длинами этих отрезков, стремящихся к нулю. Следовательно, по теореме Кантера (о вложенных отрезках) для всех отрезков найдётся такая точка х, что она принадлежит всем отрезкам (n)(xn). Однако, (n) хх_n (т.к.всегда выбирали отрезки, не содержащие очередных членов посл-ти). В итоге получили, т.х [0,1], х – действит.число, но х не совпадает ни с одним членом выбранной последоват-ти → противоречие достигается тем, что все действит.числа отрезка уложились в последоват-ть (х_n) множ-во дейст.чисел из отрезка [0,1] несчётно.

4.Множ-во мощности континуума. Примеры. Множ-во действ.чисел отрезка [0,1] несчётно, про него говорят, что оно имеет мощность континуума, которая обозначается С. Из этогочто все множ-ва, эквивалентные отрезку [0,1] попадают в класс эквивалентности, определяемый мощностью С мощность множ-ва всех действ.чисел = С. R=C. ([0,1]~(0,1); (0,1)~(- ;)) [0,1]~(-;). Если представить что R=QI, то I=R\Q. Мощность Q=α, мощность R=C, мощность I=C, R=AT, А - алгебраические числа, Т – трансценднтные. Мощность А=α, Т=R\A,→ мощность Т=С. Т.е.множ-во трансц.и иррац-х чисел имеют мощность=С. Св-ва множ-в, имеющих мощность континуум:

1˚Объединение счётного мн-ва множ-в мощности С имеет мощность С. (Объединение конечного множ-ва множ-в мощностью С имеет мощность С). Док-во: Р! посл-ть (х_n), монотонно возрастающую, (х_n) [0,1). Р! полуинтервалы вида: [0,x₁) [x₁,x₂)…[x_n-1,x_n)…=[0,1). Мощность Аn=C, [0,x₁)~A₁, [x₁,x₂)~A₂, [x_n-1,x_n)~A_n A_n. По транзитивности отношения эквивал-ти, св-во док-но.

2˚Мн-во всех подмнож-в счётного множ-ва имеет мощность континуума.

3˚Мн-во всех последоват-й нат.чисел имеет мощность континуум. Док-во:(n₁, n₂, …, n_k, …) – произв.послед-ть нат.чисел. Легко убедится в том, что множ-во всех последоват-й нат.чисел б.эквивалентно множ-ву всех монотонно возрастающих последоват-й нат.чисел. Для этого дост-но установить взаимнооднозначное соответствие. (n₁, n₂, …, n_k, …) ↔ (n₁,(n₁+n₂),(n₁+n₂+n₃),…) Док-во след-т из 2˚.

4˚ Если элементы мн-ва А определяются n-значками, каждый из которых не зависимо от других пробегает всё множ-во мощности континуум, то и мощность мн-ва А=С. Следствие: множ-во всех точек пл-ти имеет мощность С.Следствие 2: мн-во всех точек 3-хмерного простр-ва имеет мощность С. Следствие3: мн-во всех точек n-мерного евклидова простр-ва имеет мощность С.

5.Сравнение мощностей. Бесконечные множ-ва м.иметь разные мощности. Теорет-ки возможны след.случаи: Пусть даны А, В. 1)А~В, мощ.А=мощ.В 2) А₁, А₁А, А₁~B мощ.А>мощ.В, при условии, что Ане~В 3) В₁, В₁B, В₁~А →мощ.А<мощ.В, если А не ~В.4) Для мн-в А и В мн-во (В₁, В₁В, В₁~А; А₁, А₁А, А₁~В) А~В, мощ.А=мощ.В. 5) Во мн-ве А и В такая стр-ра, что невозможно указать собств.подмнож-во каждого из них, эквивалентное другому мн-ву. Итак, для мощностей 2-х беск.мн-в возвожны след,3 случая: мощ.А=мощ.В, мощ.А<мощ.В, мощ.А>мощВ. В связи с вопросом о сравнении мощностей, прведём теорему о мощности промежуточного множ-ва. Если для мн-в АА₁А₂, при чём А~А₂ м.док-ть А~А₁, мощА=мощА₁.Мощ-ть мн-ва всех подмн-в. мы научились сравнивать мощности. Из этого что мощ-ть континуума > мощ-ти счёт-го мн-ва. Воз-т вопрос, ли мн-во большей мощности чем континуум. Ответ, да, . Докажем, что мн-ва, сколь угодно большой мощности. Т:мощ-ть мн-ва всех подмнож-в -го непустого мн-ва > мощ-ти этого мн-ва. Замечание: теорема очевидна для случая конечных мн-в, т.к.для конечного мн-ва, состоящего из n-элементов, кол-во всех его подмн-в содержит 2ⁿ элементов. А={x,y,z},, {x},{y},{z},{x,y},{x,z},{y,z},{x,y,z}.2³=8. Пусть А это непустое беск.мн-во, т.к.Аρ(А),мощ ϸ(А)>мощА. Остаётся док-ть: что ϸ(А) не ~А. Док-во проведём от противного. Предположим, что мн-во ϸ(А) ~А, при а↔b, где аА, b ϸ(А). Обозначим за «плохой»элемент – эл-т, кот.не входит во мн-во, «хороший»элемент – входит. Убедимся в том, что есть как «хорошие» так и «плохие» элементы. «Хотошим», н-р, б.элемент, соотв-й всему мн-ву А. «Плохим» б.такой эл-т из мн-ва А, кот.соотв-т пустому мн-ву. Рмн-во всех «плохих» элем-в. Возникает вопрос, каким, «хорошим» или «плохим», б.элемент а, соотв-й этому множ-ву плохих элементов. Если бы он был «хорошим», то он обязан бы был войти в это подмн-во, но там содержится только «плохие» элементы. Если бы он был «плохим», он бы не вошёл в соотв.ему подмн-во. Однако, он обязан туда войти. Возникло противоречие и ϸ(А)не~А. главный итог теоремы: мн-во сколь угодно большой мощности.

6.Метрические пространства. Примеры. В основе большинства структур матанализа Р! - х нами ранее для множ-ва R лежит понятие предельного перехода. С этим понятием связаны такие понятия как непрерывность, диф-цирование и интегрирование. Понятие предельного перехода описывалось с пом-ю спец.символов ε, δ и не требовало всего мн-ва св-в действ-х чисел. Поэтому представляет интерес Р!-ние мн-ва объектов качественной природы, лля кот-х м.б.введено понятие окрестности. Так возникает определение топологического пространства – множ-во, в кот-м имеет смысл говорить о наиболее общей форме, о открытых и замкнутых множ-вах, о предельных точках, о непрерывности изображений и т.д. Предположим, что для какого то мн-ва М удаётся, благодаря наличию определённых свойств объектов этого мн-ва, ввести понятие окрестности, удовлетворяющее всем св-вам топологического простр-ва Тогда все св-ва топологических пространств автоматически переносятся на это М и м.исполнятся в дальнейшем. Так происходит, н-р, в нормированных простр-вах – множ-вах точек, для кот-х определено понятие норм или в метрических пространствах – множества точек, для кот-х определено понятие метрики или рас-я. Основ.определения. Множ-во объектов произвольной природы б.называть абстрактным материальным пространством, а его элементы б.называть точками. Метрич-м пр-вом назовём произвольное мн-во М, а его элементы наз-м точками, если для -й пары эл-в х и у из этого мн-ва М определено число ρ(х,у), называемое расстоянием, для кот-го справедливы св-ва: 1˚,уМ, ρ(х,у)≥0, при чём ρ(х,у)=0х=у.2˚х,уМ, ρ(х,у)=ρ(у,х). 3˚х, у, z М, ρ(х,у) ≤ ρ(x,z)+ρ(z,y). Др.словами, ρ(х,у) наз-ся метрикой. Ясно, что для одного и того же мн-ва М расстояние м.выводится по разному, в этом случае б.возникать раз.метрич.пространства.1)Rⁿ, n–мерное евклидово пространство. х(х₁,х₂,..,х_n), у(у₁,у₂,..у_n). ρ(х, у) ==. 2)Гильбертово пространство l₂ - это мн-во числовых посл-тей, обладающих св-вом

Метрика в этом простр-ве = ρ(x,y)=. М.убедится что все аксиомы метр.пр-ва выполнены. 3)Пр-во С_[a,b] – пр-во ф-ций, непрерывных на [a,b]. (y=у₁(х) С_[a,b] , y=y₂(x) С_[a,b]) ρ(у₁,у₂)= max(у₁(х)-у₂(х)). Покажем, что для метр.пр-ва м.б.введено понятие окрестности. ε-окрестностью точки х₀ в метр.пр-ве М назовём мн-во точек хМ, для кот-х вып-ся: ρ(х,х₀)<ε. Т.е.если это определение применить к пр-ву R², то окруж-ю б.мн-во точек, лежащих внутри окр-ти радиуса ε. Окрестностью точки х₀ наз-ся всякое открытое множ-во, содержащее данную точку. Точка х наз-ся граничной точкой множ-ва Е, если -я, сколь угодно малая окрестность этой точки содержит как точки, принадлежащие множ-ву Е, так и не принадлежащие. Совокупность граничных точек множ-ва наз-ся границей.