3.10. Операции над нечеткими множествами.

1. Дополнение. Пусть нечеткие множества A и B имеют единое базовое множество E. Нечеткое множество B является дополнением нечеткого множества A, (записывается B = A), если

x  E: _B(x) = 1 - _A(x).

Например, если

A = {(x₁0.2), (x₂0.7), (x₃1), (x₄0.4), (x₅0)},

то

A = {(x₁0.8), (x₂0.3), (x₃0), (x₄0.6), (x₅1)}.

2. Объединение. Объединением двух нечетких множеств A и B, заданных на одном и том же базовом множестве E называется нечеткое множество C = A  B, содержащее и A и B, причем функция принадлежности определяется по правилу

х  E: _C(х) = max(_A(х),_B(х))

Пример 2. Пусть A = {(x₁0.4), (x₂0.7), (x₃0.9)} и B = {(x₁0.5), (x₂0.3), (x₃1)}.

Тогда C = A  B = {(x₁0.5), (x₂0.7), (x₃1)}.

3. Пересечение. Пересечением двух нечетких множеств A и B, заданных на одном и том же базовом множестве E называется нечеткое множество D = A  B, содержащие и A и B, причем функция принадлежности определяется по правилу

x E: _D(x) = min(_A(x),_B(x)).

Для нечетких множеств из примера 2 имеем

D = A  B = {(x₁0.4), (x₂0.3), (x₃0.9)}

Наглядное представление операций объединения и пересечения двух нечетких множеств заданных на непрерывном подмножестве дают схемы, родственные диаграммам Вьенна - Эйлера, которые представлены на рис. 3.10. Границы штрихованных областей изображают графики функций принадлежности соответствующих нечетких множеств.

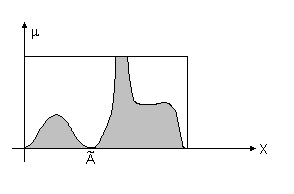
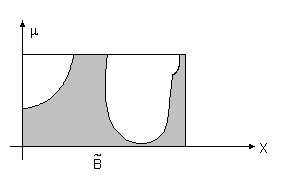
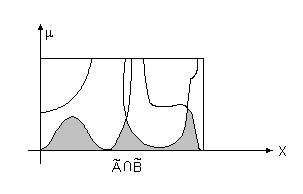
Рис. 3.10. Иллюстрация операций объединения и пересечения нечетких множеств.

4. Произведение. Произведением двух нечетких множеств A  B, заданных на одном и том же базовом множестве E называется такое нечеткое множество

F = AּB, функция принадлежности которого определяется по правилу

x  E: _F(x) = _A(x)ּ_B(x)

Для нечетких множеств из примера 2 имеем

F = AּB = {(x₁0.2), (x₂0.21), (x₃0.90}

5. Сумма. Суммой двух нечетких множеств A и B, заданных на одном и том же базовом множестве E называется нечеткое множество H = A + B, содержащие множества A и B, причем функция принадлежности определяется по правилу

х  E: _H(х) = _A(х) + _B(х) - _A(х)ּ_B(х)

Для нечетких множеств из примера 2 имеем

H = A + B = {(x₁0.7), (x₂0.79), (x₃1)}.

Замечание. Операции умножения и суммирования нечетких множеств употребляются значительно реже, чем операции пересечения и объединения, поскольку для них не выполняются некоторые свойства, в том числе и такое, как дистрибутивность.

6. Разность. Разностью двух множеств A и B, заданном на одном и том же базовом множестве E, называется нечеткое множество G = A - B = A  B, причем функция принадлежности определяется по правилу

х  E: _G(х) = min(_A(х), 1 - _B(х))

Для нечетких множеств из примера 2 имеем

G = A - B = {(x₁0.47), (x₂0.7), (x₃0.1)}.

7. Возведение в степень. Пусть задано нечеткое множество A, заданное на базовом множестве E. Возведением в неотрицательную степень "" нечеткого множества A называется нечеткое множество K = A^, функция принадлежности которого _K(х) определяется по правилу

_K(х) = (_A(х))^

Возведение нечеткого множества в квадрат называется операцией концентрирования

A²  CON(A).

Извлечение корня квадратного из нечеткого множества, рассматриваемого как возведение в степень 0.5, называется операцией растяжения

A^0.5 = DIL(A).

Так, например, если

A = {(x₁0.4), (x₂0.7), (x₃0.9)},

то

CON(A) = {(x₁0.16, (x₂0.49), (x₃0.81)},

DIL(A) = {(x₁0.63), (x₂0.84), (x₃0.95)}.

Нечетким евклидовым расстоянием между двумя нечеткими множествами A и B называется величина

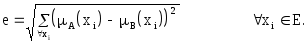
Ближайшим к данному нечеткому множеству A называется четкое множество A, расположенное на наименьшем евклидовом расстоянии от A. Это множество определяется функцией принадлежности, формируемой по правилу

Пример 3. Пусть заданы два множества:

A = {(x₁0), (x₂0.1), (x₃0.3), (x₄0.7), (x₅0.8), (x₆0.9), (x₇1)}

и

B = {(x₁0), (x₂0), (x₃0), (x₄0.6), (x₅0.8), (x₆1), (x₇1)}.

Тогда e(AB) = 0.346, а ближайшее к нечеткому множеству A является четкое множество A = {(x₁0), (x₂0), (x₃0), (x₄1), (x₅1), (x₆1), (x₇1)}.

В теории нечетких множеств имеет место принцип обобщения, который можно записать следующим образом:

f({x_A(x)}) = {f(x)_A(x)}

где A - нечеткое множество; f - некоторое отображение X  Y.

Например, если y = x² + 3 и A = {(10.4), (20.6), 30.9}, то f(A) = {(40.4), (7.0.6), (120.9)}.

Этот принцип открывает возможности вводить функциональные описания на нечетких множествах, что имеет важное значение в приложениях теории нечетких множеств.