3.7. Пример построения динамической модели

Для иллюстрации процесса построения математической модели рассмотрим пример решения широко известной задачи динамки популяции. В 1798 Мальтус опубликовал свою работу, посвященную проблеме ¹выживаемости человечества и содержащую соответствующую математическую модель. В ее основе лежит предположение о том, что изменение численности популяции пропорционально исходному объему популяции (численность популяции на момент времени ), рассматриваемому промежутку времени и некоторому обобщенному коэффициенту - коэффициенту рождаемости, т.е. . Заметим, что это характерный пример линейного мышления.

В этой связи простейшая математическая модель Мальтуса для оценки темпа роста численности популяции организмов, размножающихся при постоянных условиях выглядит следующим образом [11].

Это обыкновенное дифференциальное уравнение, решение которого при , имеет вид

.

Если ввести показатель мгновенной смертности d (коэффициент смертности), то модель приобретает вид

Решение этого уравнения (изменение численности популяции во времени) есть функция

Величина служит мерой, определяющей скорость роста популяции. Если , то популяция в данный момент сокращается, а при возрастает.

На продолжительном отрезке времени смертность и рождаемость могут значительно изменяться, т.е. быть функцией времени . В этом случае

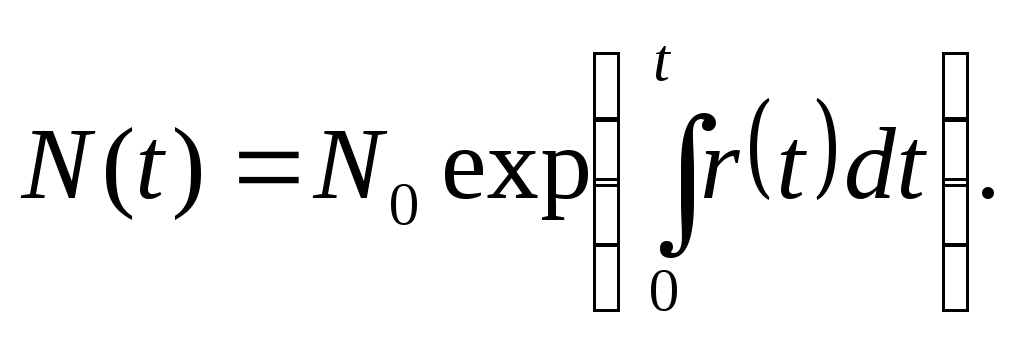
При численность популяции устойчива. В противном случае величина изменяется по экспоненциальному закону, т.е. даже малые отклонения от устойчивого состояния могут привести к неограниченному росту (или исчезновению) популяции. В реальной же действительности существуют некоторые внутренние механизмы, регулирующие численность популяции. Эффективность этих механизмов часто зависит от численности популяции на данный момент. Учет такого механизма приводит к следующей модели

В частном случае, если - максимальная численность популяции, которую может обеспечить окружающая среда и изменение скорости роста популяции пропорционально величине , то модель примет вид

.

Это уравнение имеет решение

которое достаточно хорошо описывает изменение численности популяции и может использоваться на практике.

В природе часто встречаются ситуации, когда численность популяций одних видов взаимосвязана с численностью другой популяции. Подобные межвидовые отношения также можно моделировать системой дифференциальных уравнений. Так для двух взаимосвязанных видов имеем

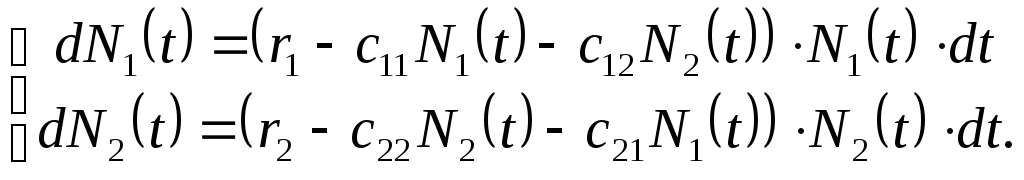
где описывает влияние численности видов на их собственные скорости роста, есть мера подавления вида видом (.

Данный пример иллюстрирует возможность применения аппарата дифференциальных уравнений для исследования проблем народонаселения, численности популяций животного мира, применяться при описании боевых действий и т.п.

Рассмотрим вариант модели, применяемый в системах массового обслуживания. Пусть в каждый момент времени система может находиться в одном из следующих состояний: . Предположим, что за малый интервал времени , непосредственно следующий за , система может остаться в данном состоянии или перейти только в одно из "соседних" состояние, т.е. в - более высокое или в - более низкое. Пусть интенсивность перехода в более высокое состояние есть , а в более низкое . Требуется определить - изменение каждого из возможных состояний время.

Изменение данного состояния за малое время складывается из следующих составляющих:

1. Переход из нижнего состояния в верхнее: и ;

2. Переход из верхнего состояния в нижнее: и .

Исключения составляют лишь граничные состояния и : из можно прейти только в , а из только в .

Эти рассуждения позволяют составить следующую систему разностных дифференциальных уравнений.

(7)

Система уравнений (7) представляет модель "размножения и гибели", получившая свое название при изучении проблемы изменения численности популяций в биологии. С точки зрения математики (7) - это система обыкновенных дифференциальных уравнений, решение которой позволит определить функцию, описывающую динамику состояния системы. Так может означать на данный момент времени число людей в данном городе, число частиц в атомном реакторе, вероятность занятости каналов связи на данной телефонной станции и т.п.

Здесь не рассматриваются модели математического программирования, поскольку методики их построения близки к тому, что изложено выше.