
- •4. Вычисление вероятностей сложных событий. Теоремы сложения и умножения вероятностей. Условная вероятность
- •5. Формула полной вероятности и формула Байеса
- •6. Повторение опытов
- •Общая теорема о повторении опытов
- •4.3. Варианты заданий для контрольной работы № 5 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •4.4. Методические указания к выполнению контрольной работы № 6
- •1. Случайные величины и их законы распределения
- •Ряд распределения
- •Функция распределения
- •Плотность распределение
- •2. Числовые характеристики случайных величин
- •3. Некоторые законы распределения случайных величин Равномерное распределение
- •Биномиальный закон распределения. Закон Пуассона
- •Показательное (экспоненциальное) распределение. Функция надежности
- •4. Закон больших чисел
- •Предельные теоремы теории вероятностей
- •4.5. Варианты заданий для контрольной работы № 6 Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •5. Учебно-методическое обеспечение дисциплины
- •5.1. Литература обязательная
- •Математика
- •Часть III. Элементы теории вероятностей
- •Светлана Владимировна Рожкова
- •Рецензент: к. П. Арефьев, д. Ф.-м. Н., профессор каф. Вм енмф
2. Числовые характеристики случайных величин
Математическим
ожиданием случайной
величины
![]() называется ее среднее значение,
вычисляемое по формулам:
называется ее среднее значение,
вычисляемое по формулам:
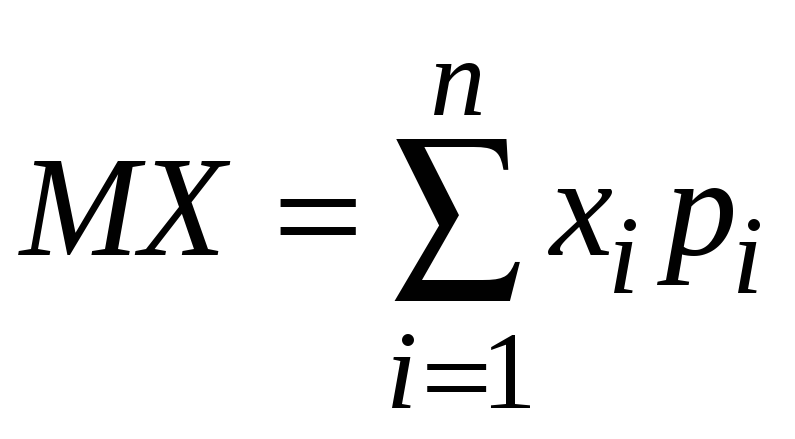 – для
дискретной случайной величины;
– для
дискретной случайной величины;
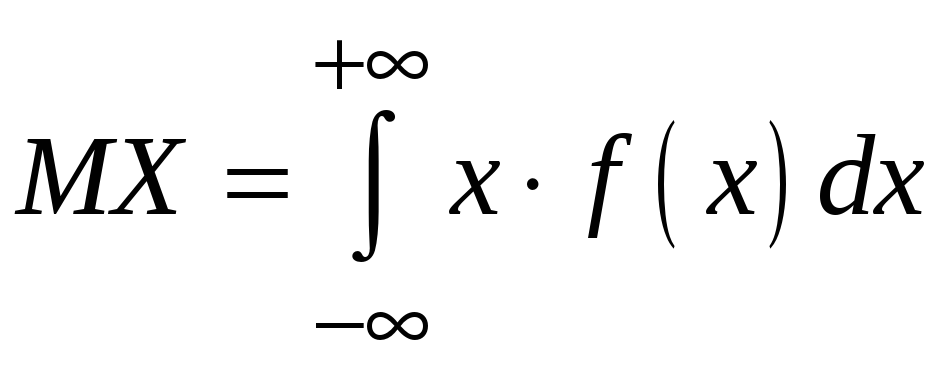 – для
непрерывной случайной величины.
– для
непрерывной случайной величины.
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
![]() .
.
Обозначим
![]() ,
тогда формулы для вычисления дисперсии:
,
тогда формулы для вычисления дисперсии:
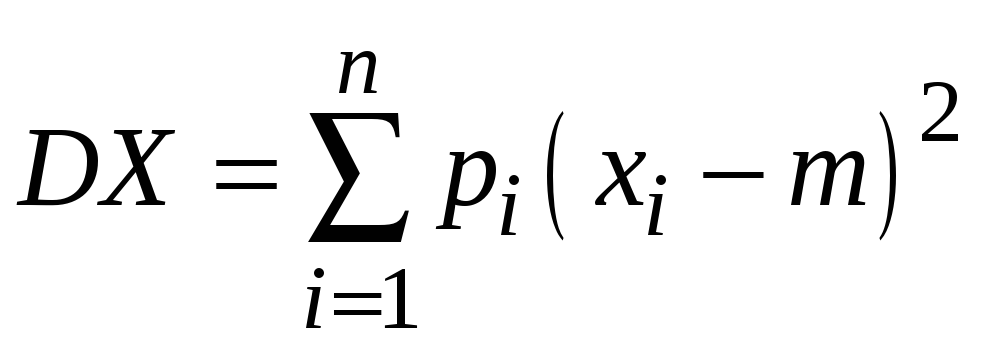 ;
;
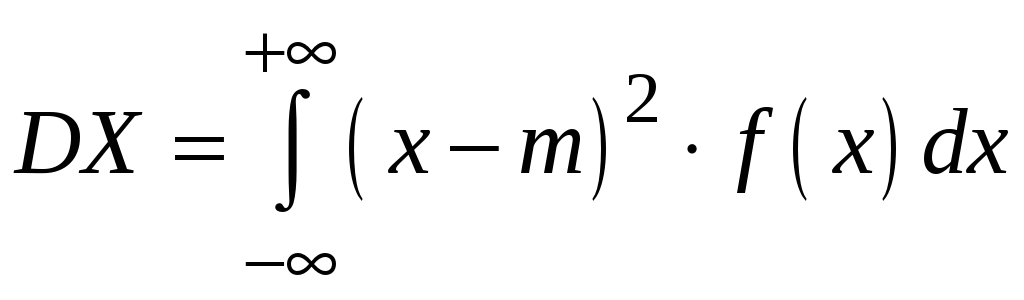 .
.
Средним
квадратическим отклонением
![]() случайной величины
случайной величины
![]() называется корень квадратный из ее
дисперсии:
называется корень квадратный из ее
дисперсии:
![]() ,
,
![]() .
.
Пример 1.
Случайная
величина
![]() – число очков, выпавших при однократном
бросании игральной кости. Определить
– число очков, выпавших при однократном
бросании игральной кости. Определить
![]() .
.
Решение.
-
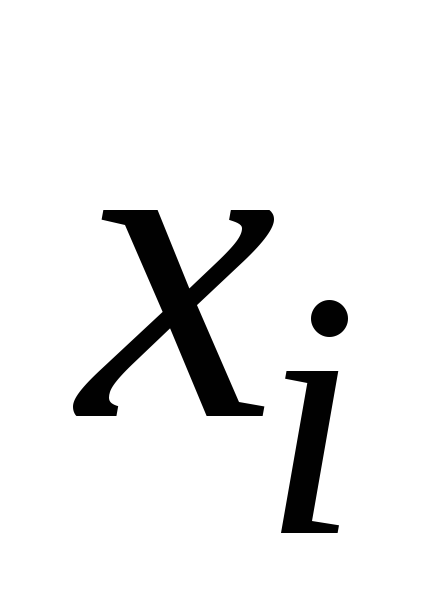
1
2
3
4
5
6
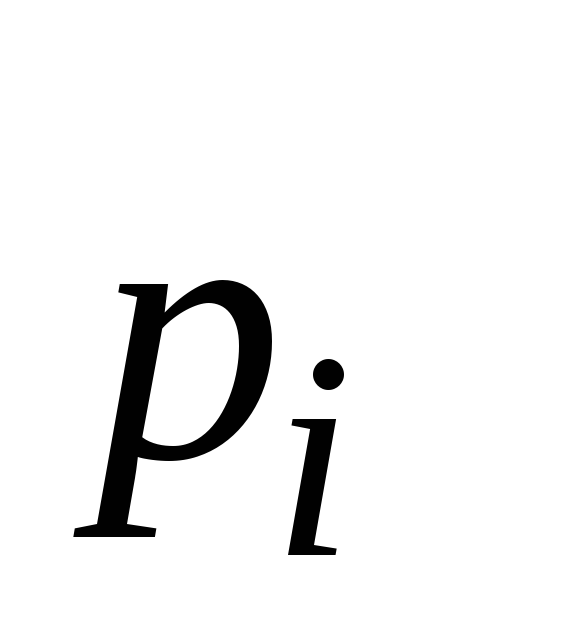
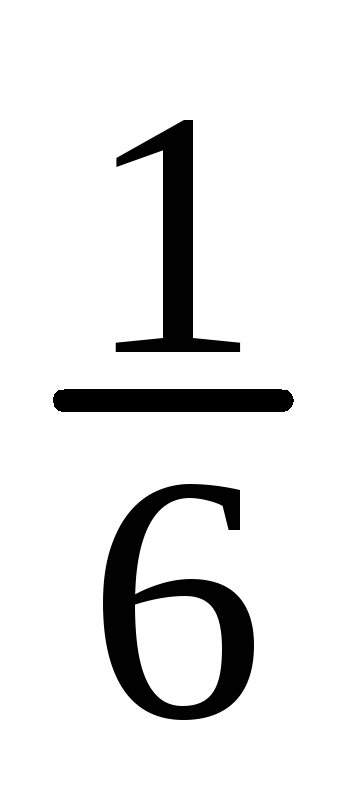
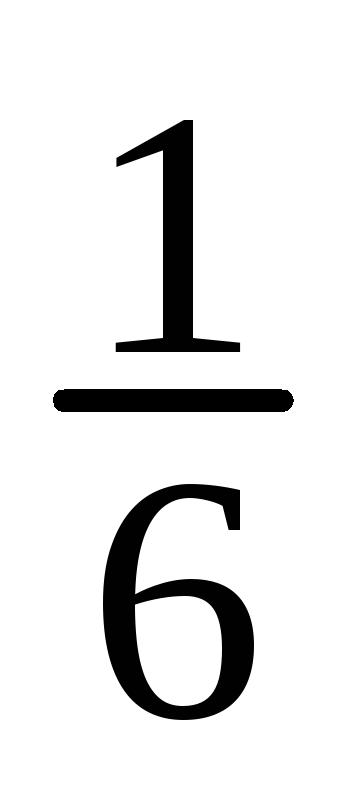
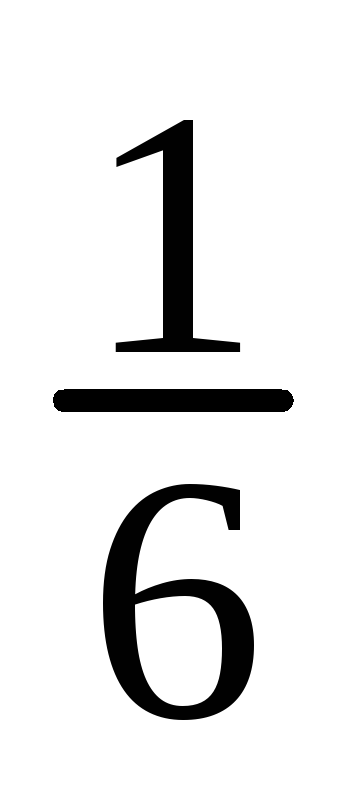
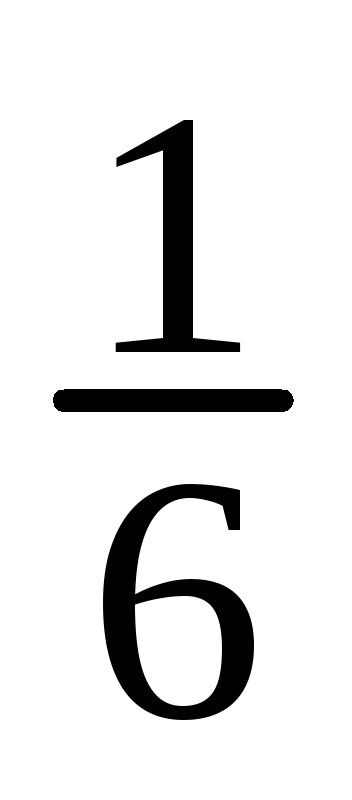
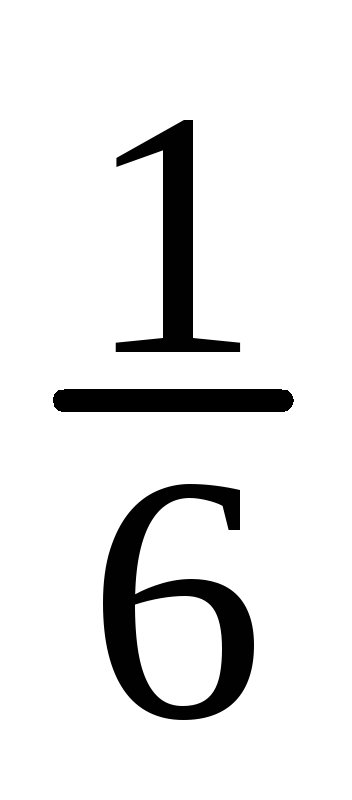
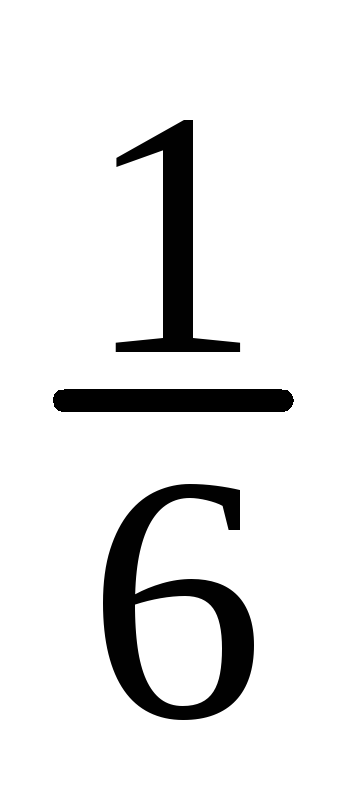
Имеем
![]() ;
;
![]()
![]() .
.
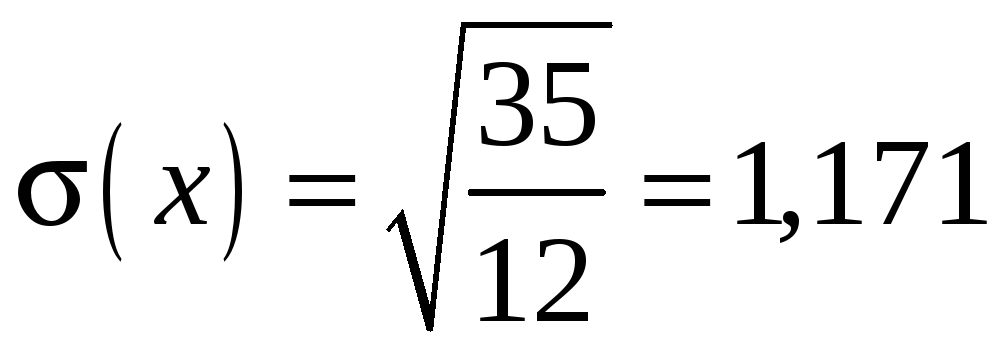 .
.
Пример 2.
Дана
функция
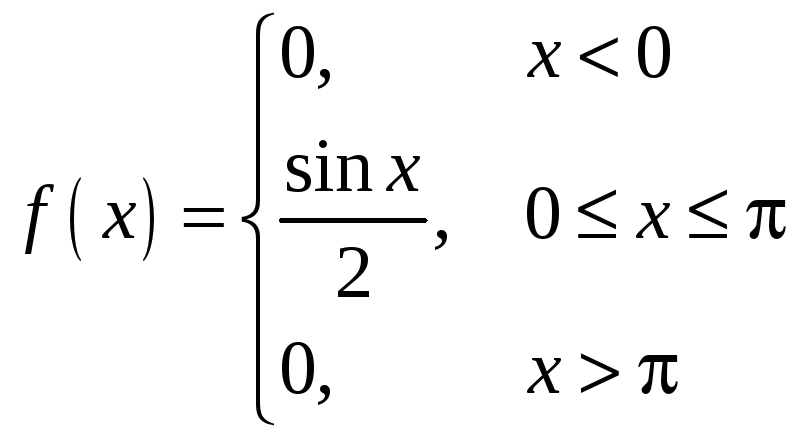 .
Показать, что
.
Показать, что
![]() может служить плотностью распределения
вероятностей
некоторой
случайной величины
может служить плотностью распределения
вероятностей
некоторой
случайной величины
![]() .
Найти
.
Найти
![]() .
.
Решение.
Имеем
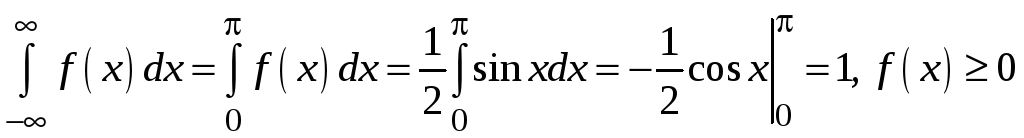 .
.
Следовательно,
![]() может служить плотностью распределения
некоторой случайной величины.
может служить плотностью распределения
некоторой случайной величины.

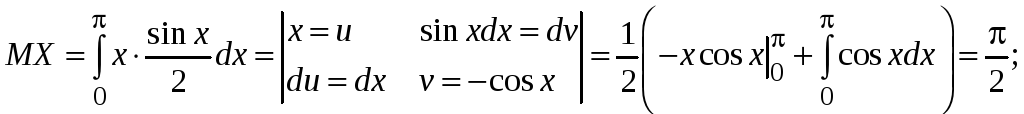
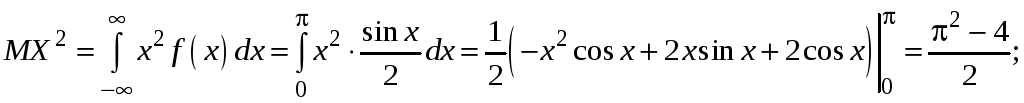
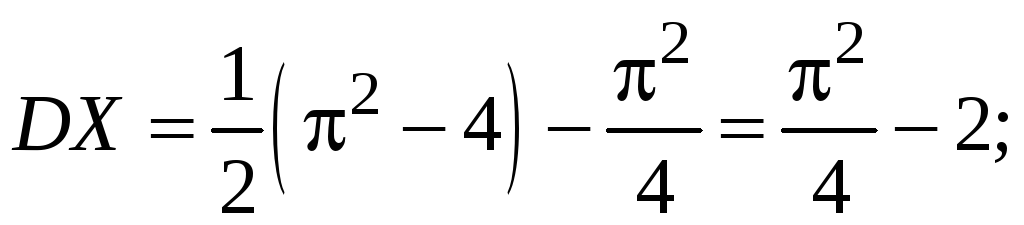
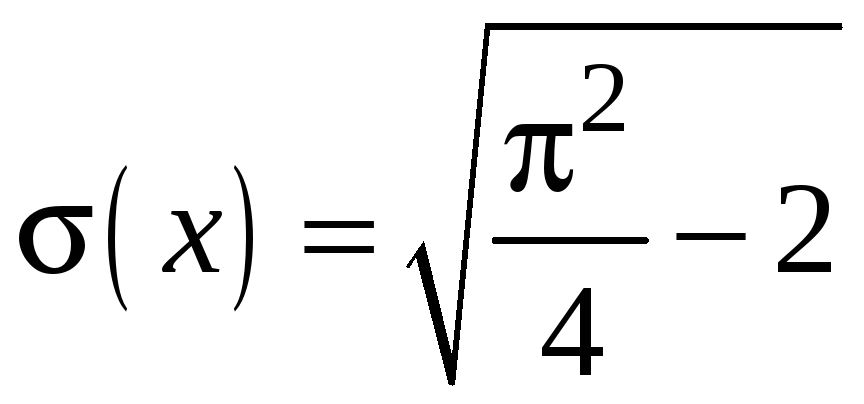 .
.
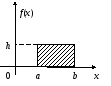
3. Некоторые законы распределения случайных величин Равномерное распределение
Равномерным
называется распределение таких случайных
величин, все значения которых лежат на
![]() и имеют постоянную плотность вероятности
на этом отрезке.
и имеют постоянную плотность вероятности
на этом отрезке.
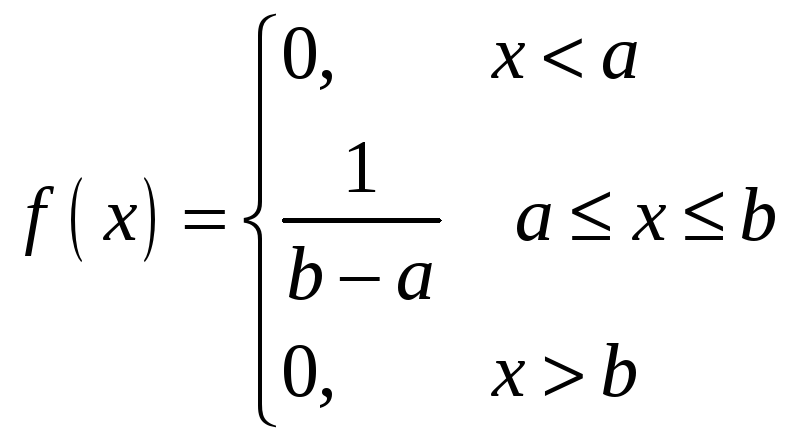 .
.
Функция распределения этого закона распределения имеет вид:
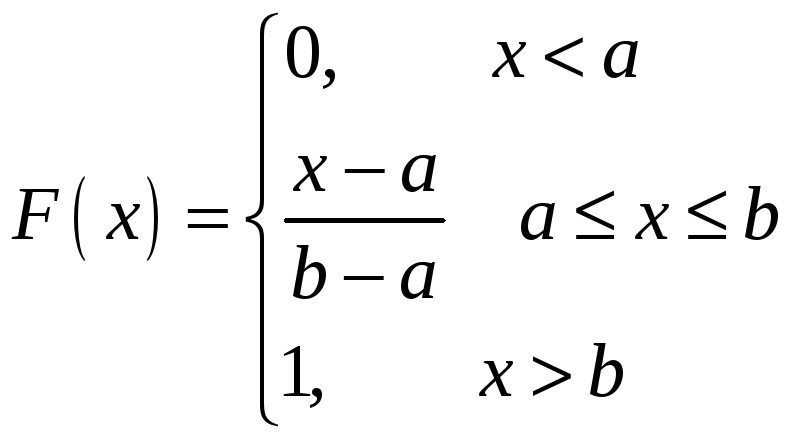 ;
;
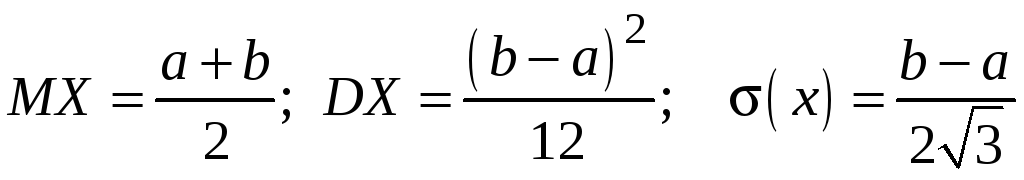 .
.
Пример 1.
Случайная
величина – отклонение емкости конденсатора
от номинала распределено на отрезке
![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Построить график
.
Построить график
![]() .
.
Решение.
В
задаче
![]() ,
поэтому
,
поэтому
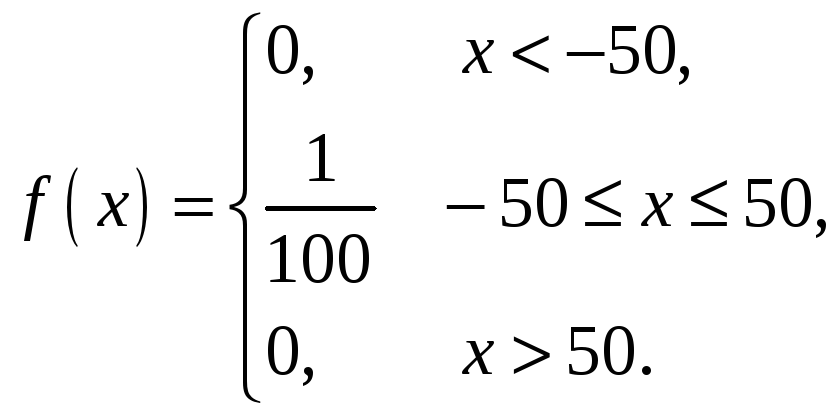
Построим график f(x).
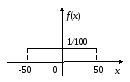
Функция распределения вероятности случайной величины:
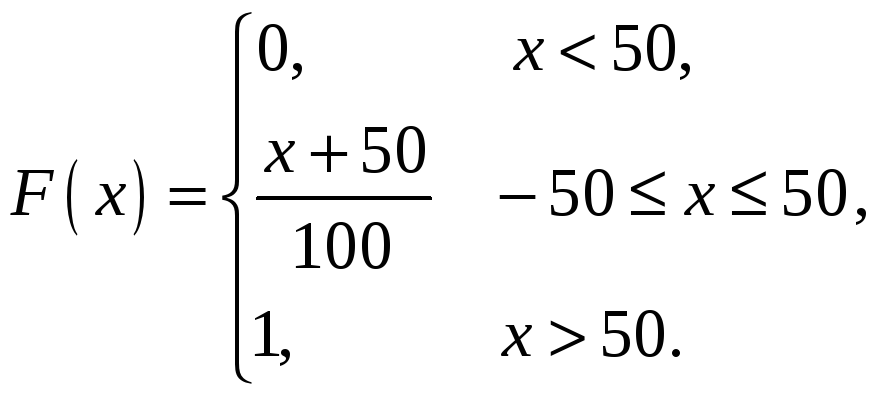
Ее график имеет вид:
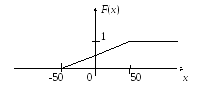
![]() ,
,
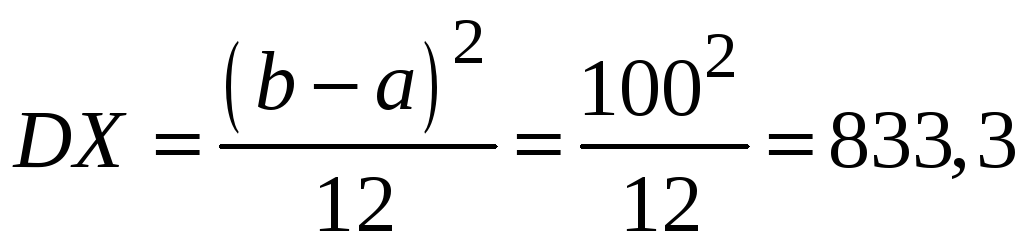 ;
;
![]() .
.
Биномиальный закон распределения. Закон Пуассона
Если
вероятность наступления случайного
события в каждом испытании равна
![]() ,
то, как известно, вероятность того, что
при
,
то, как известно, вероятность того, что
при
![]() испытаниях событие осуществляется
испытаниях событие осуществляется
![]() раз, определяется формулой Бернулли:
раз, определяется формулой Бернулли:
![]() .
.
Закон
распределения случайной величины
![]() ,
которая может принимать
,
которая может принимать
![]() значение
значение
![]() ,
описывается формулой Бернулли, называется
биномиальным.
,
описывается формулой Бернулли, называется
биномиальным.
Закон
распределения случайной величины
![]() ,
которая может принимать любые целые
неотрицательные значения
,
которая может принимать любые целые
неотрицательные значения
![]() ,
описываемый формулой
,
описываемый формулой
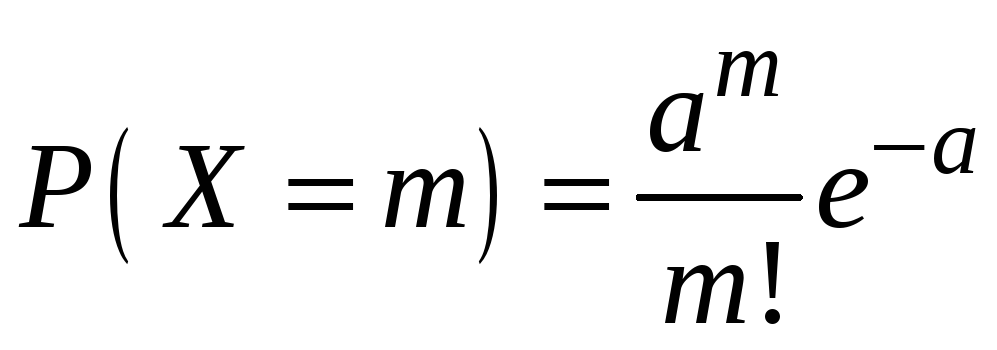 ,
носит название Пуассона.
,
носит название Пуассона.
Для
биномиального закона
![]() ;
;
![]() .
.
Для
закона Пуассона:
![]() .
.
Пример 1.
Производится
три независимых опыта, в каждом из
которых событие
![]() появляется с вероятностью 0,4. рассматривается
случайная величина
появляется с вероятностью 0,4. рассматривается
случайная величина
![]() – число появлений события
– число появлений события
![]() в трех испытаниях. Построить ряд
распределения и функцию распределения
случайной величины
в трех испытаниях. Построить ряд
распределения и функцию распределения
случайной величины
![]() .
Найти
.
Найти
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Ряд распределения:
-
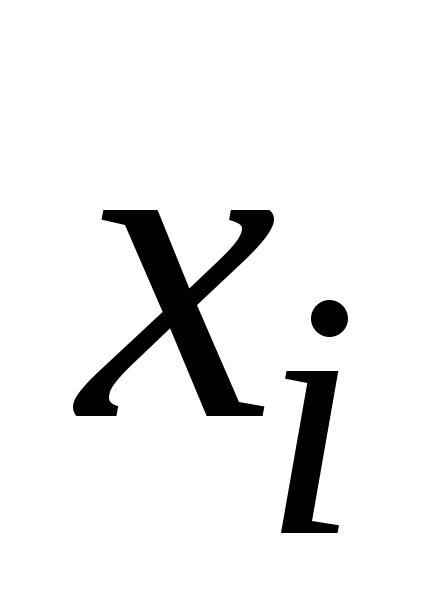
0
1
2
3
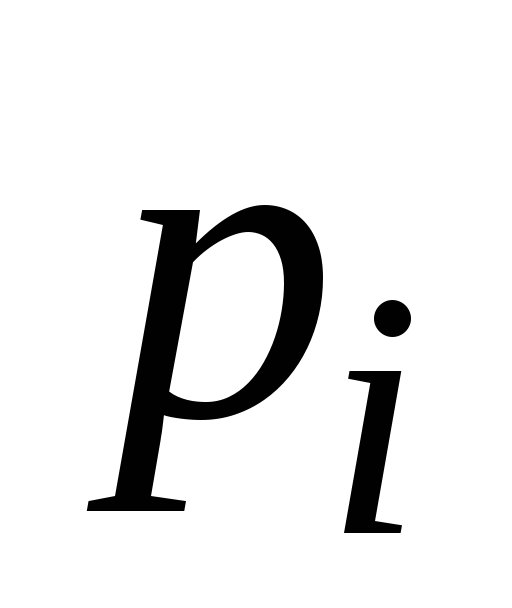
0,216
0,432
0,288
0,064
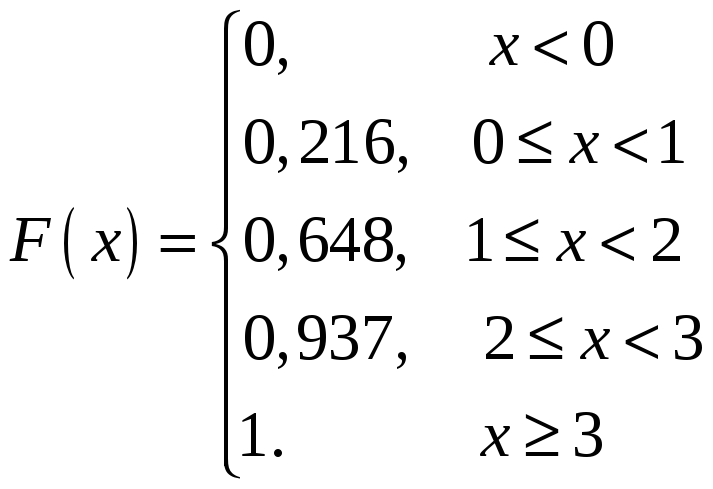
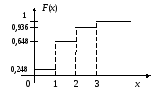
![]() ;
;
![]()
![]() .
.
Пример 2.
Радиоаппаратура состоит из 100 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равно 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и менее двух электроэлементов за год?
Решение.
Считая
случайное число
![]() отказавших элементов подчиняющихся
закону Пуассона
отказавших элементов подчиняющихся
закону Пуассона
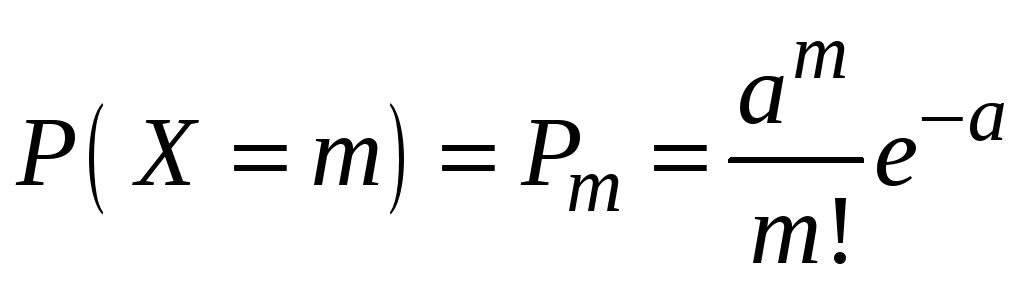 ,
где
,
где
![]() ,
получим:
,
получим:
-
вероятность отказа ровно двух элементов
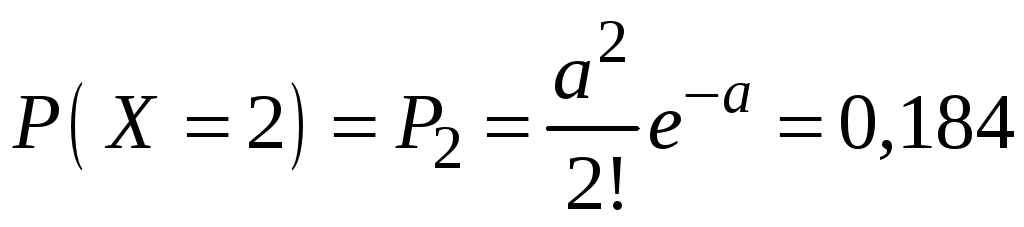 ;
;
-
вероятность отказа не менее двух элементов
![]() ;
т.е.
;
т.е.
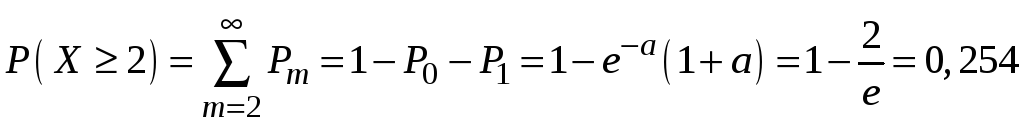 .
.
