4. Вычисление вероятностей сложных событий. Теоремы сложения и умножения вероятностей. Условная вероятность

Теорема 1. (Сложения вероятностей)

Вероятность суммы двух совместных событий и равна сумме вероятностей этих событий без вероятности их совместного наступления

.

Вероятность суммы несовместных событий рвана сумме их вероятностей, т.е.

.

Эта теорема обобщается на случай произвольного числа попарно несовместных событий: .

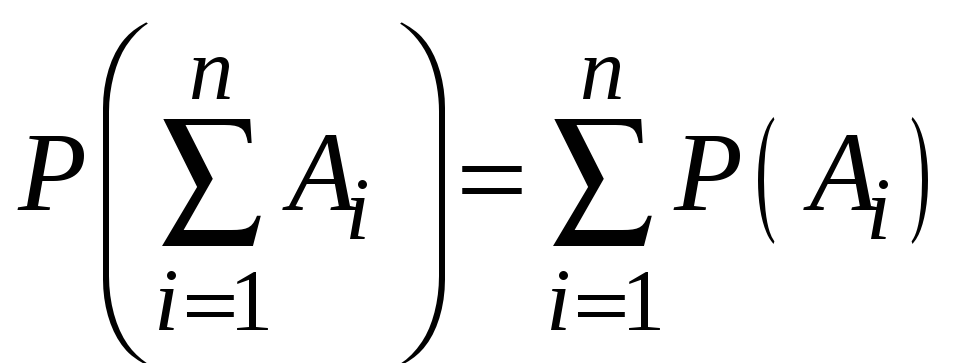События и называются независимыми, если вероятность не зависит от того, произошло событие или нет.

Событие называется зависимым от события , если вероятность события зависит от того, произошло или не произошло событие .

Вероятность события , вычисленная при условии, что имело место, называется условной вероятностью .

Теорема 2. (Умножения вероятностей)

Вероятность произведения двух зависимых событий и равна произведению вероятности одного их этих событий на условную вероятность другого, при условии, что первое наступило:

.

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

.

Обобщенная теорема умножения:

.

Вероятность произведения событий, независимых в совокупности, равна произведению вероятностей этих событий:

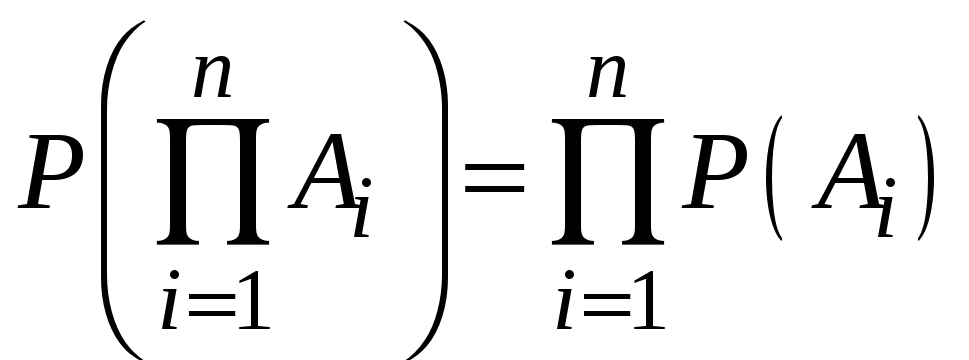
Пример 1.

Три стрелка независимо друг от друга стреляют по цели Вероятность попадания в цель для первого стрелка − 0,75; для второго − 0,3; для третьего − 0,9. Найти вероятность того, что все три стрелка попадут в цель.

Решение.

Пусть событие – первый стрелок попал в цель; событие – второй стрелок попал в цель; событие – третий стрелок попал в цель;

– все три стрелка попадут в цель.

.

Пример 2.

Идет бомбардировка трех складов боеприпасов. Сбрасывают одну бомбу. Вероятность попадания в первый склад равна 0,01; во второй равна 0,008; в третий − 0,025. При попадании в любой их них взрываются все. Найти вероятность того, что склады будут взорваны.

Решение.

Событие – взрыв складов; – попадание в первый склад; – попадание во второй склад; – попадание и третий склад.

, так как несовместны, то:

.

Пример 3.

Имеется три ящика, содержащих по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Решение.

Вероятность того, что из первого ящика вынута стандартная деталь (событие ) равна .

Вероятность того, что из второго ящика вынута стандартная деталь (событие ) равна .

Вероятность того, что из третьего ящика вынута стандартная деталь (событие ) равна .

Так как события , и независимы, то искомая вероятность события (по теореме умножения) равна

.

Пример 4.

Вероятности появления каждого из трех независимых событий , , соответственно равны , , Найти вероятность появления только одного из этих событий.

Решение.

Заметим, что, например, появление только первого события , равносильно появлению события (появилось первое и не появились второе и третье события).

Обозначим: – появление только события , т.е. ;

– появление только события , т.е. ;

– появление только события , т.е. .

Таким образом, чтобы найти вероятность появления только одного из событий , , , воспользуемся теоремой сложения несовместных событий: .

Определим вероятности каждого из событий .

События , , – независимы, поэтому

_,,,

и тогда

.

Пример 5.

Вероятность попадания в цель при стрельбе из трех орудий соответственно равны , , . Найти вероятность хотя бы одного попадания (событие ) при одном залпе из всех орудий.

Решение.

Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий.

Рассмотрим события;

– попадание первым орудием;

– попадание вторым орудием;

– попадание третьим орудием.

; ; ; ; ; ;

.

Пусть событие – хотя бы одно попадание, а – ни одрого попадания, тогда .

Событие , тогда .

и .

Пример 6.

Из урны, содержащей белых и черных шаров, вынимают два шара. Какова вероятность того, что они будут разных цветов?

Решение.

Представим событие , состоящее в том, что вынуты шары разных цветов, в виде , где событие состоит в том, что первый шар −белый, а второй − черный, событие состоит в том, что первый шар − черный, а второй − белый. Так как события и несовместны, то .

Тогда .

Аналогично , .

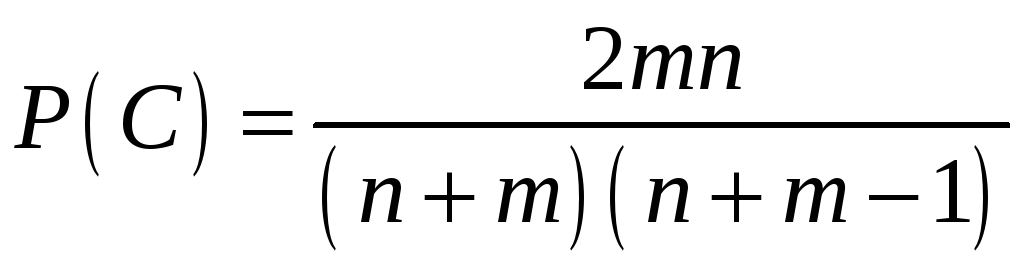Ответ: .

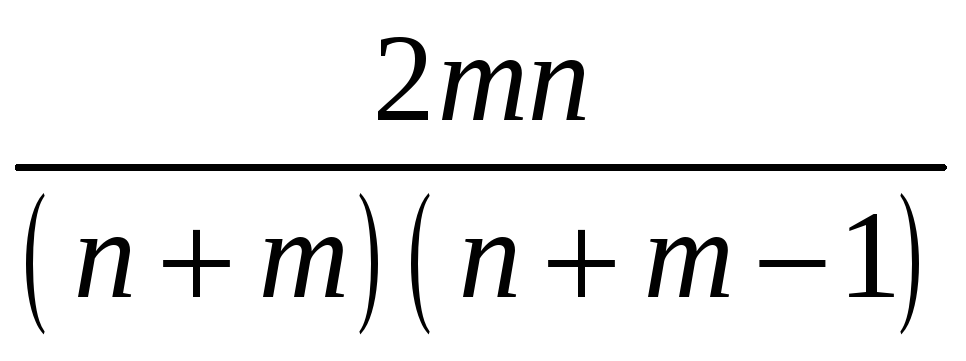Пример 7.

Бросаются две монеты. Рассматриваются события: – выпадение герба на первой монете, – выпадение герба на второй монете. Найти вероятность события .

Решение.

Так как и – несовместны, то

,

или через противоположное событие .

Пример 8.

Система состоит из двух дублирующих блоков , и управляющего устройства – блока . В случае исправности блока работает блок ; если блок выходит из строя, управляющее устройство включает блок . Если блок не исправен, то он не включает блок . Известны вероятности блоков , . Найти надежность системы, если блоки независимые.

Решение.

Обозначим – события, состоящие в том, что блоки и система соответственно исправны.

1 решение. Система будет исправна, если исправен или блок или оба блока и , или все три блока.

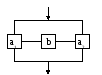
Тогда , ,

.

2 решение. Воспользуемся понятием противоположного события. Система неисправна, если неисправен блок и хотя бы один из блоков или , т.е.

,

; ; ;

;

.

Пример 9.

Среди 12 аппаратов четыре первого тина и восемь второго. Случайным образом из них выбирают три аппарата последовательно (без возвращения). Найти вероятность того, что при первом и третьем будут выбраны, аппараты второго типа, а вторым – аппарат первого типа.

Решение.

Пусть – выбран первый аппарат, – выбран второй аппарат, – выбран третий аппарат.

По классической формуле 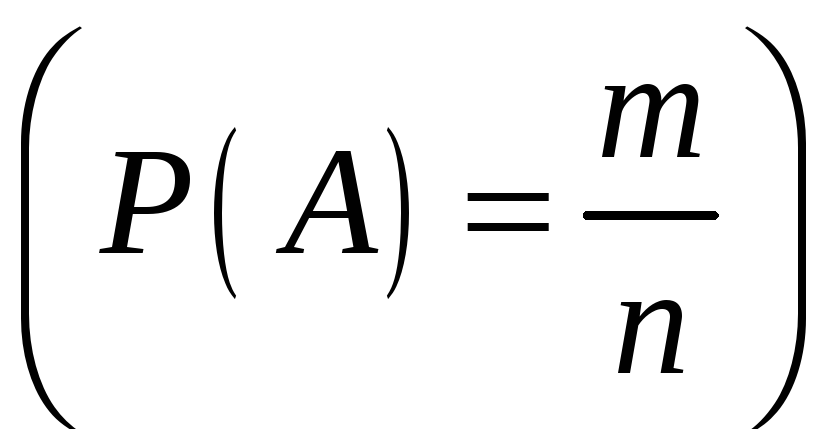определим, т. е. первый аппарат второго типа; , т.е. второй аппарат первого типа, а всего аппаратов осталось 11; , т. к. третий аппарат второго типа, а их осталось 7, и всего аппаратов 10.

.