
- •4. Вычисление вероятностей сложных событий. Теоремы сложения и умножения вероятностей. Условная вероятность
- •5. Формула полной вероятности и формула Байеса
- •6. Повторение опытов
- •Общая теорема о повторении опытов
- •4.3. Варианты заданий для контрольной работы № 5 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •4.4. Методические указания к выполнению контрольной работы № 6
- •1. Случайные величины и их законы распределения
- •Ряд распределения
- •Функция распределения
- •Плотность распределение
- •2. Числовые характеристики случайных величин
- •3. Некоторые законы распределения случайных величин Равномерное распределение
- •Биномиальный закон распределения. Закон Пуассона
- •Показательное (экспоненциальное) распределение. Функция надежности
- •4. Закон больших чисел
- •Предельные теоремы теории вероятностей
- •4.5. Варианты заданий для контрольной работы № 6 Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •5. Учебно-методическое обеспечение дисциплины
- •5.1. Литература обязательная
- •Математика
- •Часть III. Элементы теории вероятностей
- •Светлана Владимировна Рожкова
- •Рецензент: к. П. Арефьев, д. Ф.-м. Н., профессор каф. Вм енмф
Показательное (экспоненциальное) распределение. Функция надежности
Аналогом закона Пуассона для непрерывных случайных величин служит показательный закон распределения, функция плотности распределения которого имеет вид
 ,
где
,
где
![]() постоянный параметр.
постоянный параметр.
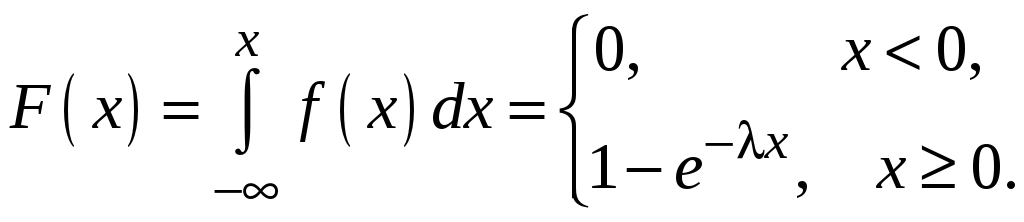 ;
;
![]() ,
,
![]() ,
,
![]() ;
;
![]() .
.
Если
![]() – непрерывная случайная величина,
выражающая продолжительность безотказной
работы какого-либо элемента, а
– непрерывная случайная величина,
выражающая продолжительность безотказной
работы какого-либо элемента, а
![]() – среднее число отказов в единицу
времени (интенсивность отказов), то
продолжительность времени
– среднее число отказов в единицу
времени (интенсивность отказов), то
продолжительность времени
![]() безотказной работы этого элемента можно
считать случайной величиной, распределенной
по показательному закону распределения
с функцией распределения
безотказной работы этого элемента можно
считать случайной величиной, распределенной
по показательному закону распределения
с функцией распределения
![]() ,
,
которая
определяет вероятность отказа элемента
за время
![]() ,
а
,
а
![]() называется функцией надежности.
называется функцией надежности.
Пример 1.
Время
![]() телефонного разговора – случайней
величина, распределенная по показательному
закону распределения с параметром
телефонного разговора – случайней
величина, распределенная по показательному
закону распределения с параметром
![]() .
Записать
.
Записать
![]() .
Найти
.
Найти
![]() ,
,
![]() .
Определить вероятность того, что разговор
будет продолжаться более трех минут.
.
Определить вероятность того, что разговор
будет продолжаться более трех минут.
Решение.

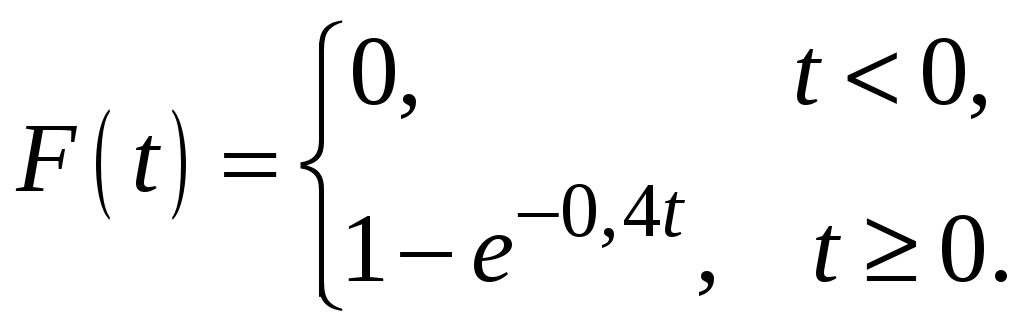
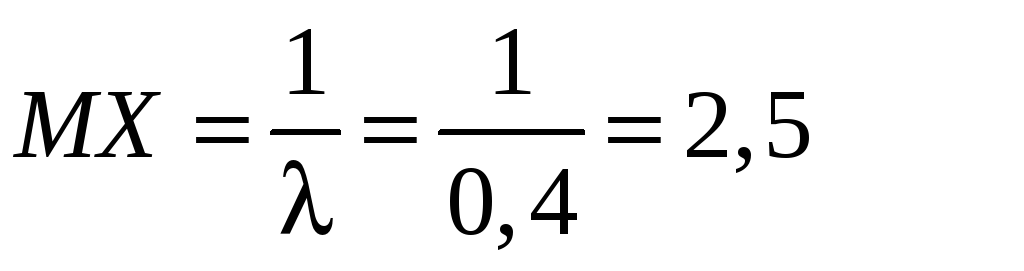
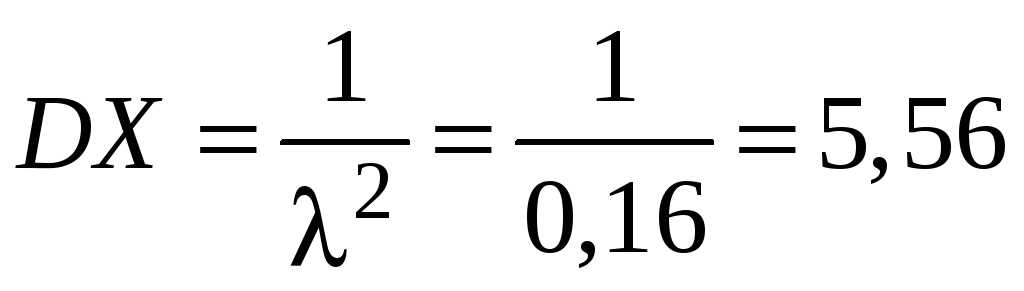 ;
;
![]() .
.
Пример 2.
Непрерывная
случайная величина
![]() распределена
по показательному закону:
распределена
по показательному закону:
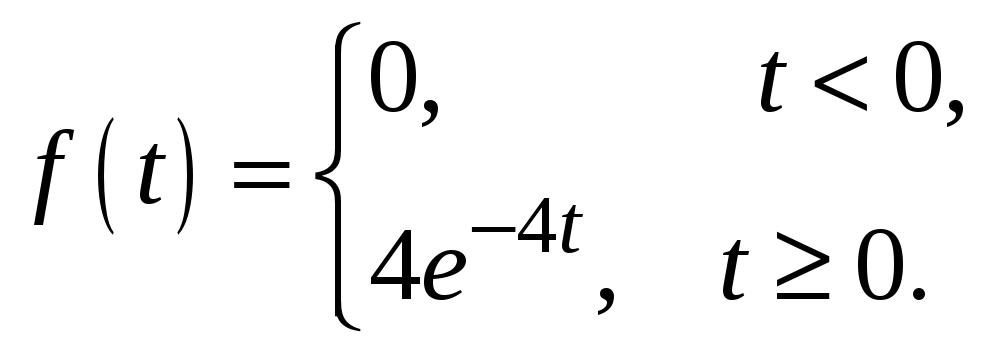 .
Найти вероятность того, что в результате
испытаний
.
Найти вероятность того, что в результате
испытаний
![]() попадет в интервал
попадет в интервал
![]() .
.
Решение.
По
формуле
![]() имеем
имеем
![]() .
.
Нормальный закон распределения. Функция Лапласа
Нормальный закон распределения характеризуется плотностью
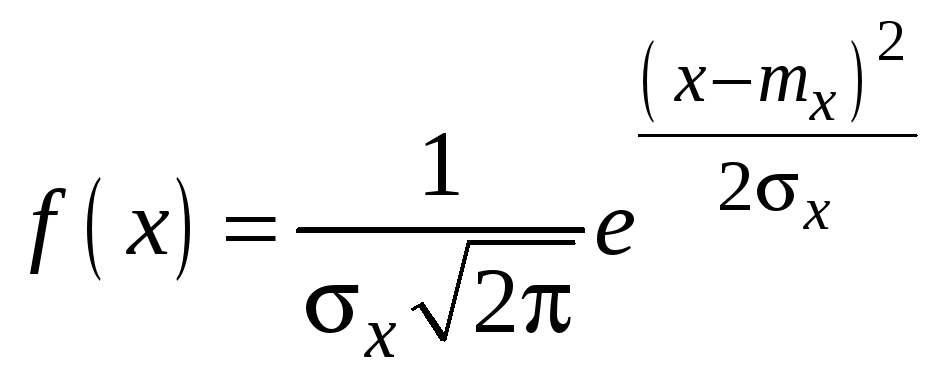 ,
,
где
![]() – математическое ожидание случайной
величины;
– математическое ожидание случайной
величины;
![]() – среднее квадратичное отклонение
величины
– среднее квадратичное отклонение
величины
![]() .
.
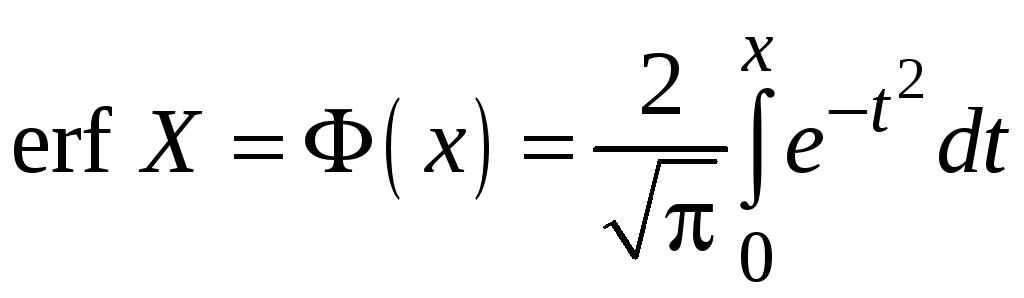 – называется
функцией Лапласа, или интеграл
вероятностей, функция ошибок.
– называется
функцией Лапласа, или интеграл
вероятностей, функция ошибок.
Иногда используют другие формы функции Лапласа, например,
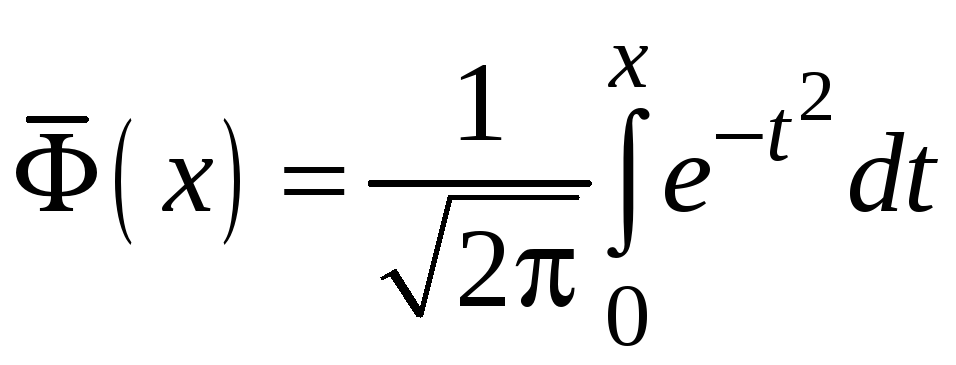 – нормированная
функция Лапласа.
– нормированная
функция Лапласа.
 ;
;
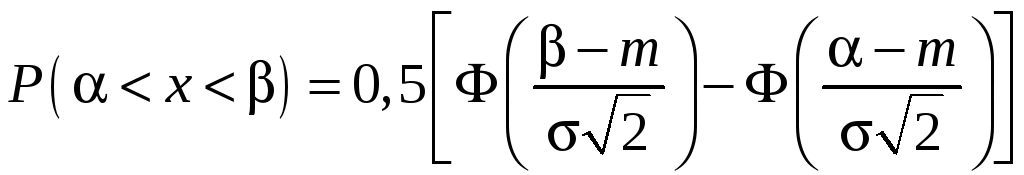 .
.
Отметим следующие свойства функции Лапласа:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
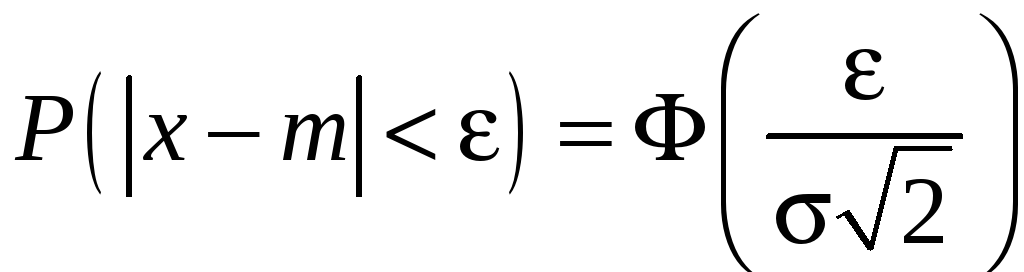 .
.
Пример 1.
Пусть
случайная величина
![]() распределена
по нормальному закону с математическим
ожиданием
распределена
по нормальному закону с математическим
ожиданием
![]() и
и
![]() .
Найти вероятность того, что
.
Найти вероятность того, что
![]() примет значение принадлежащее интервалу
примет значение принадлежащее интервалу
![]() .
.
Решение.
Пользуясь
формулой
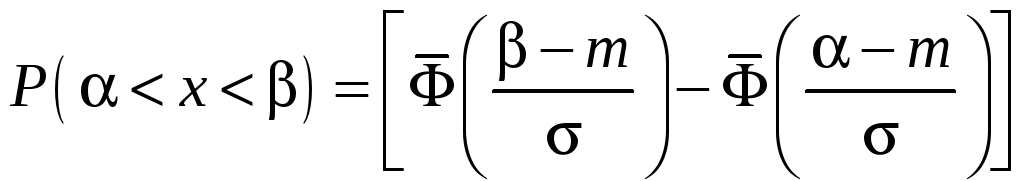 ,
получим
,
получим
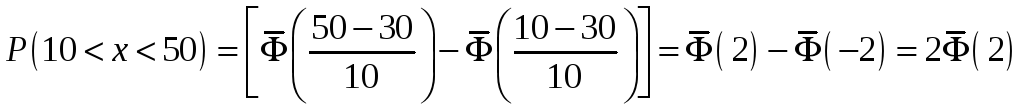 .
.
По
таблице приложения
![]() .
Отсюда искомая вероятность
.
Отсюда искомая вероятность
![]() .
.
Пример 2.
Пусть
случайная величина
![]() распределена
по нормальному закону с параметрами
распределена
по нормальному закону с параметрами
![]() и
и
![]() .
Найти
.
Найти
![]() .
.
Решение.
Используя формулу 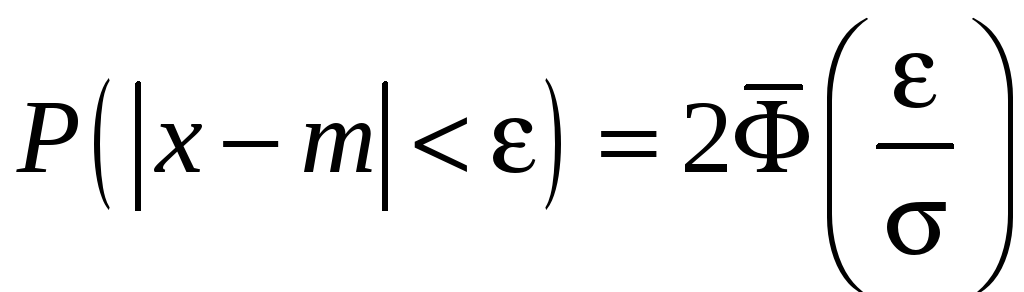 , имеем
, имеем
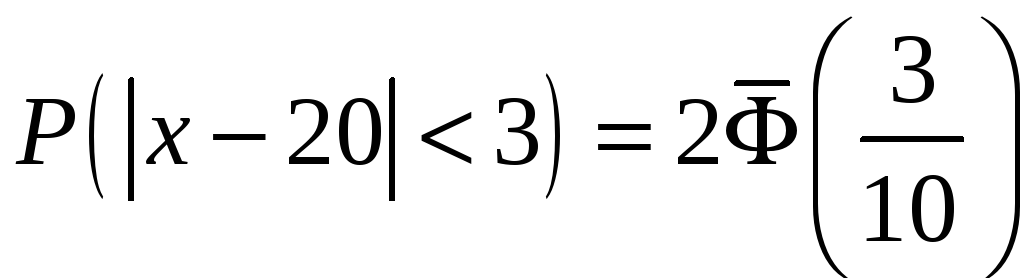 .
.
По
таблице приложения находим
![]() .
.
Поэтому
![]() .
.
Пример 3.
Случайная
величина
![]() распределена по нормальному закону с
математическим ожиданием
распределена по нормальному закону с
математическим ожиданием
![]() .
Задан интервал
.
Задан интервал
![]() ,
не включающий начало координат. При
каком значения среднего квадратического
отклонения
,
не включающий начало координат. При
каком значения среднего квадратического
отклонения
![]() вероятность
попадания в
вероятность
попадания в
![]() достигает максимума?
достигает максимума?
Решение.
Для решения задачи сделаем схематический чертеж:
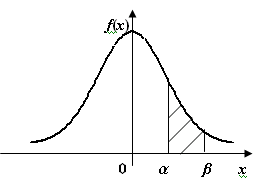
Значение
![]() найдем, дифференцируя по
найдем, дифференцируя по
![]() вероятность попадания в
вероятность попадания в
![]() и приравнивая производную к нулю. Имеем
и приравнивая производную к нулю. Имеем
 .
.
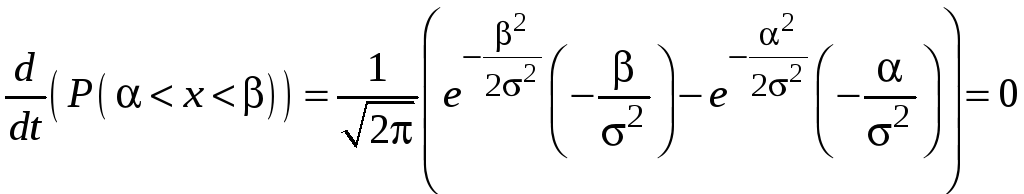 .
.
Отсюда
 ,
и, следовательно,
,
и, следовательно,
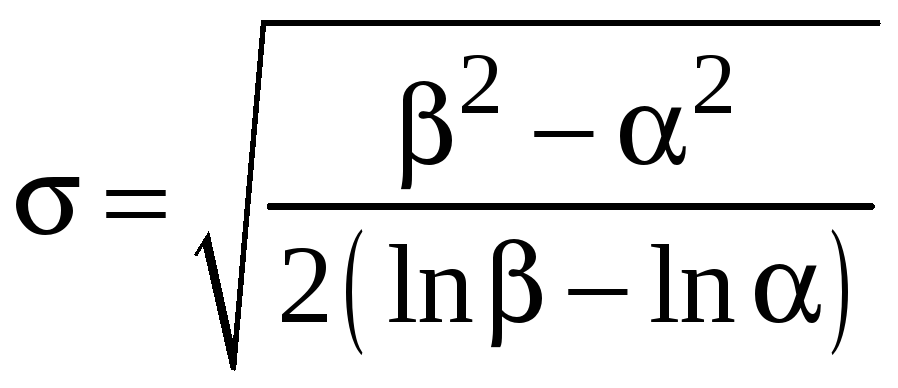 .
Для малого интервала
.
Для малого интервала
![]()
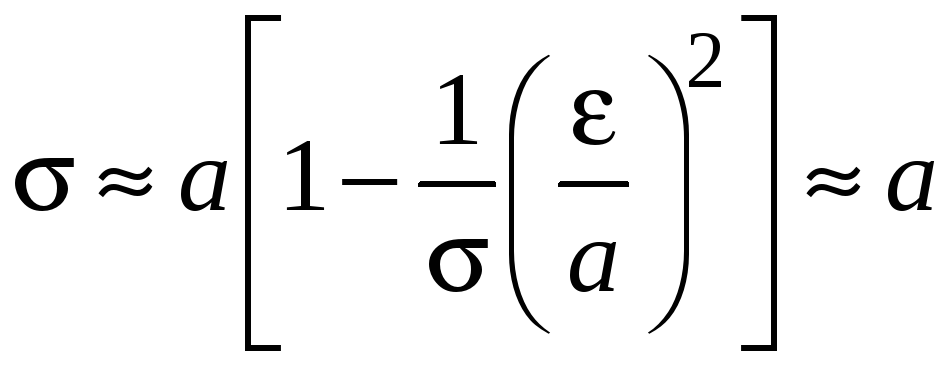 .
.
4. Закон больших чисел
Трудно сказать о том, какие значения примет случайная величина. Все зависит от совокупности случайных обстоятельств. Когда таких случайных обстоятельств очень много, то, оказывается, существуют условия, позволяющие предвидеть ход опыта, явления, которые получили название закона больших чисел или предельных теорем.
Если существует математическое ожидание квадрата случайной величины, то имеет место неравенство:
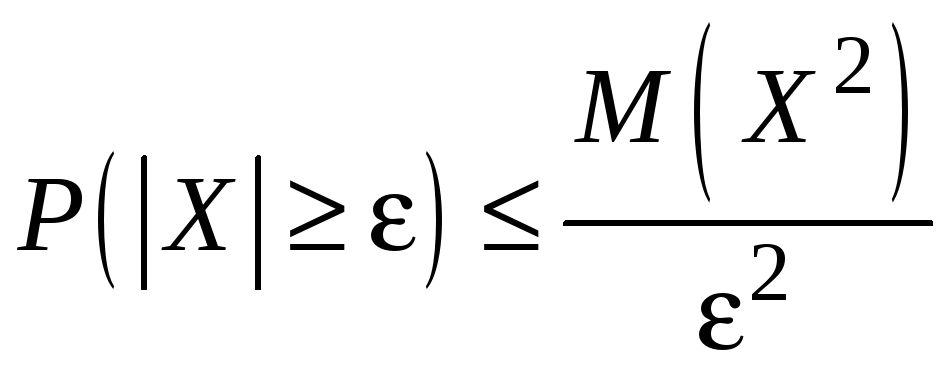 .
.
Это неравенство называется вторым неравенством Чебышева.
Первое неравенство Чебышева:
если
существует
![]() ,
то для всех
,
то для всех
![]() имеет место
имеет место
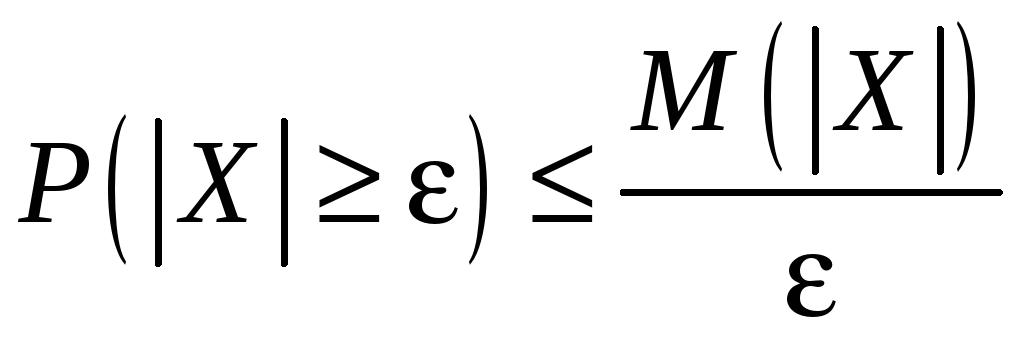 .
.
Выберем
в качестве случайной величины
центрированную случайную величину
![]() и применим к ней второе неравенство
Чебышева:
и применим к ней второе неравенство
Чебышева:
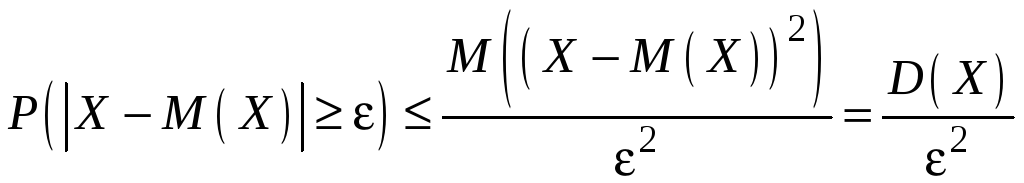 .
.
Теорема Чебышева (закон больших чисел).
Если
случайные величины в последовательности
![]() попарно независимы, а их дисперсии
удовлетворяют условию
попарно независимы, а их дисперсии
удовлетворяют условию
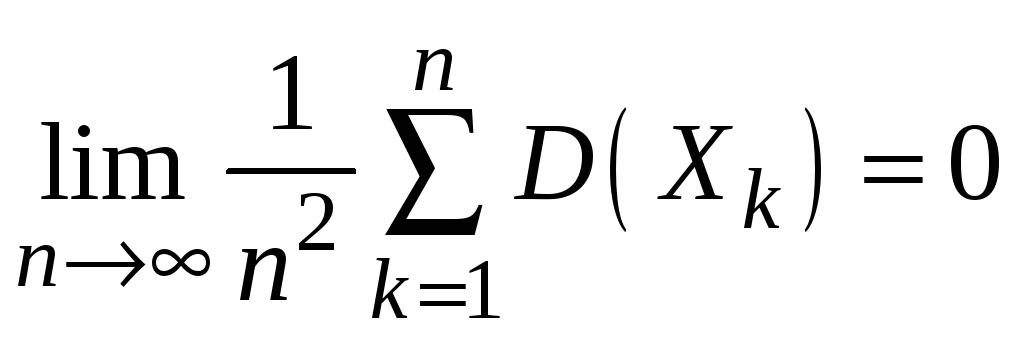 ,
то для всех
,
то для всех
![]()
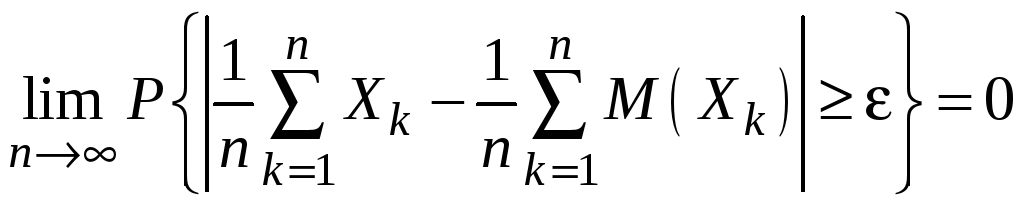 .
.
Теорема Маркова (закон больших чисел в общей формулировке).
Если
дисперсии произвольных случайных
величин в последовательности
![]() удовлетворяют условию
удовлетворяют условию
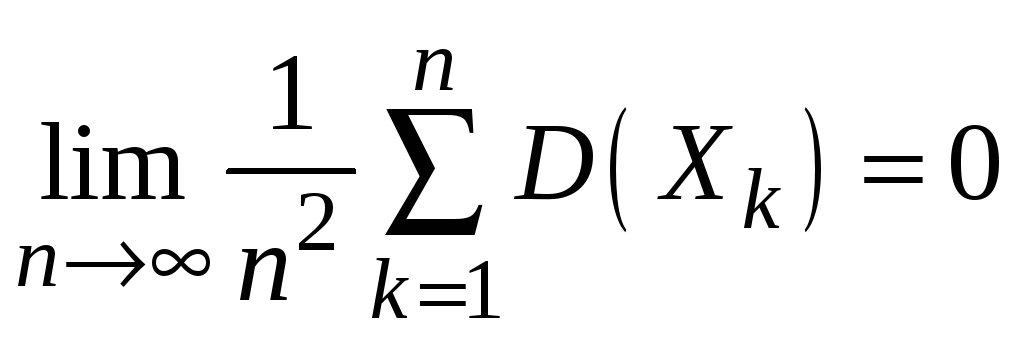 ,
то имеет место утверждение
,
то имеет место утверждение
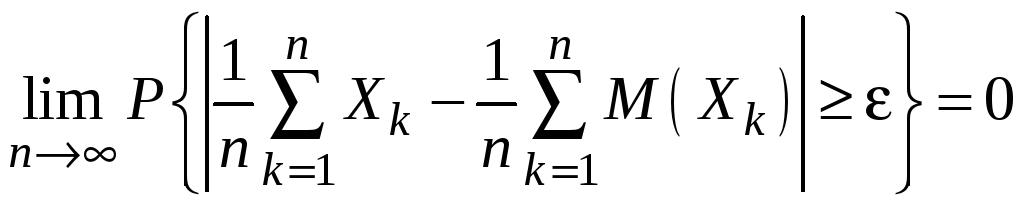 .
.
Пример 1.
Измеряется
скорость ветра в данном пункте Земли.
Случайная величина
![]() – проекции вектора скорости ветра на
фиксированное направление. Оценить
вероятность события
– проекции вектора скорости ветра на
фиксированное направление. Оценить
вероятность события
![]() ,
если путем многолетних измерений
установлено, что
,
если путем многолетних измерений
установлено, что
![]() .
.
Решение.
За
![]() возьмем 80
км/ч и,
применив первое неравенство Чебышева,
получим
возьмем 80
км/ч и,
применив первое неравенство Чебышева,
получим
![]() =>
=>
![]() .
.
